面试题：快速计算1亿内所有整数的最大奇因数和

题目描述

求1到n（n为1亿）内所有整数的最大奇因数和。
对于最大奇因数的说明，如10的最大奇因数是5；如9的最大奇因数是9本身。
要求：时间必须在1000ms内。空间要求不限。

思路

1. 和非常大。显然要使用int64。
2. 即使最简单的计算1到n的和，时间都超过1000ms。显然需要寻找低于O（N）的方法。
3. 奇数的答案是本身，偶数最快的方法是连续除2直到成为奇数为止。这是算法核心。
4. 如果没有条件限制，可以使用并行算法（如多线程、cuda加速等，不过这不属于我们讨论的范围。我们讨论纯粹的C++实现。）

算法

奇数

奇数直接累加本身。对于一亿内的所有奇数，使用等差数列求和公式解决即可：

// 1到n-1的奇数的最大奇因数和.n必须是奇数
int64_t OddSum(int64_t n)
{
    return ( (n + 1) * ((n+1)/2) ) / 2;
}

因此，奇数的时间复杂度为O（1）。

偶数

偶数是难点。最简单的方法就是连续除2直到成为奇数为止。代码如下：

// 普通计算最大因数
int MaxFactor(int n)
{
    while (0 == n % 2)
        n >>= 1;
    return n;
}

即使去除了奇数，一亿内的偶数这样去累加，仍然需要4000ms以上。

使用二进制

如果能想到二进制，快速计算最大奇因数则变得简单。
如下图，对于一个4个bit的二进制数字12，我们可以快速去除其最后的2个0，得知其最大奇因数为二进制（11），即3.

4	3	2	1
1	1	0	0

因此，一个数的最大奇因数，即为通过移位去除二进制后面的0后的结果。
现在开始考虑一亿这个数的特点。我们发现，26位二进制能表示的最大整数m=1<<26的结果为67108864。
对于[2,m)左闭右开区间中的偶数，我们可以通过分组计算方法极快的得出结果。
而对于[m,n]，还剩大概3.3kw个数。去除奇数，还剩下1.6kw个数。常规计算即可。
具体的举例来说，考虑如下一组：

26	25	…	2	1
0	0	0	1	0
…	…	…	1	0
1	1	1	1	0

注意该组的特点：其最后2位必为（10）。也就是只需要除一次2变成为奇数。
这时，3-26位之间可组成（1<<24）个不同的连续数字，可以使用等差数列公式计算结果。
同样的，在处理其他分组，如最后有2个0的，等等，一直到最后有25个0的极端情况(1<<25），此时该数的唯一奇因数是1.
这种处理方式很容易让你想到IP地址的分组。

代码

完整代码如下：

#include <iostream>
#include <stdint.h>
#include <time.h>
using namespace std;

// 普通计算最大因数
int MaxFactor(int n)
{
    while (0 == n % 2)
        n >>= 1;
    return n;
}

// 1到1-n的奇数的最大因数和.n必须是奇数
int64_t OddSum(int64_t n)
{
    return ( (n + 1) * ((n+1)/2) ) / 2;
}

// 计算27位二进制中:
// .........................10 
// .10000000000000000000000000
// n : 总位数(26)
int64_t QuickEven(int64_t n)
{
    int64_t sum = 0;
    for (int i = 24; i >= 1; --i) // i为末尾0的个数
    {
        int64_t count  = 1 << (n - i - 1);
        int64_t nStart = 1;
        int64_t nEnd   = ( ((1 << n) - 1) - ((1 << i) - 1 )) >> i;
        sum += (nStart + nEnd) * count / 2;
    }
    // 加上最后一种特殊情况：最高位为1，后面全为0.
    return sum + 1;
}

int main()
{
    // 1<<26: 67108864
    // odd : 2500000000000000
    // even: 833333333471362
    //    1: 458033364523821
    //    2: 375299968947541
    // sum :3333333333471362
    int64_t n = 100000000, m = 1 << 26;
    int64_t sum = 0, sum_odd = 0, sum_even1 = 0, sum_even2 = 0;

    time_t tbegin = clock();

    // 奇数
    sum_odd = OddSum(n-1);

    // 1<<26 内的加速算法
    sum_even1 = QuickEven(26);

    // 1<<26 到 n 之间的普通计算
    for (int64_t i = m; i <= n; i += 2)
        sum_even2 += MaxFactor(i);

    time_t tEnd = clock();
    cout << "Time use: " << tEnd - tbegin << " ms." << endl;
    cout << "odd  : " << sum_odd   << endl;
    cout << "even1: " << sum_even1 << endl;
    cout << "even2: " << sum_even2 << endl;
    cout << "sum  : " << sum_odd + sum_even1 + sum_even2 << endl;
    return 0;
}

运行结果

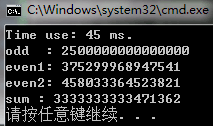
本人CPU为I7处理器，VS2013.Release模式下运行结果如下：