leetcode-代码随想录-动态规划-516最长回文子序列

最新推荐文章于 2025-11-02 11:27:35 发布

原创最新推荐文章于 2025-11-02 11:27:35 发布 · 322 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #动态规划 #算法

数据结构专栏收录该内容

163 篇文章

订阅专栏

题目

题目链接：516. 最长回文子序列 - 力扣（LeetCode）

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。
子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        
    }
};

思路

本题与647. 回文子串 - 力扣（LeetCode）
的区别：

647题：
- 统计所有回文子串数量。必须连续
- dp类型：布尔值（是否回文）
- 状态转移：首尾相同 + 内部回文
本题：
- 找最长回文子序列长度。可以不连续
- dp类型：整数值（回文长度）
- 状态转移：
  - 首尾相同：内部长度 + 2
  - 首尾不同：max(去头，去尾)

1. DP数组含义

dp[i][j]：表示字符串 s 中从索引 i 到 j（左闭右闭 [i, j]）的子串中最长回文子序列的长度。

2. 递推公式

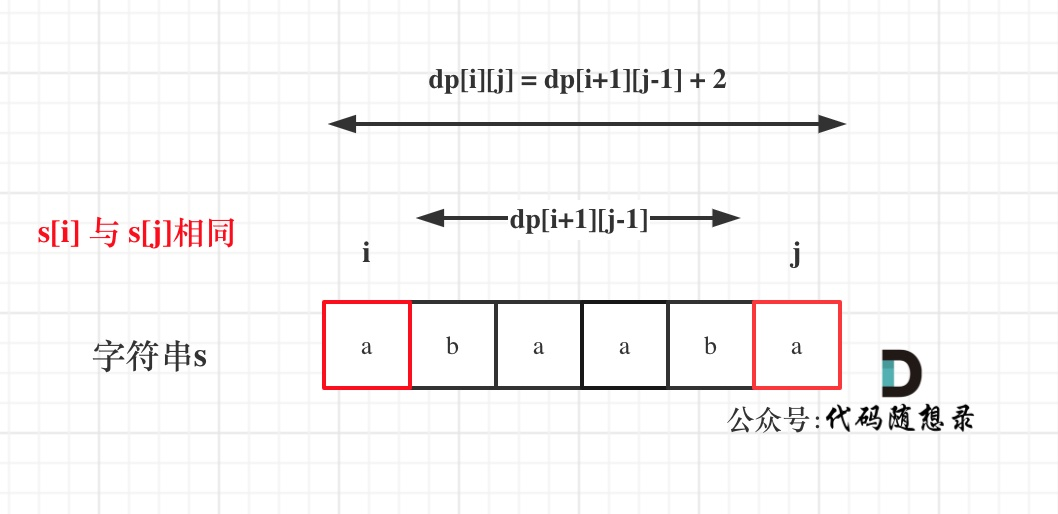
情况1：s[i] == s[j]

首尾字符相同，可以加入回文序列
dp[i][j] = dp[i+1][j-1] + 2

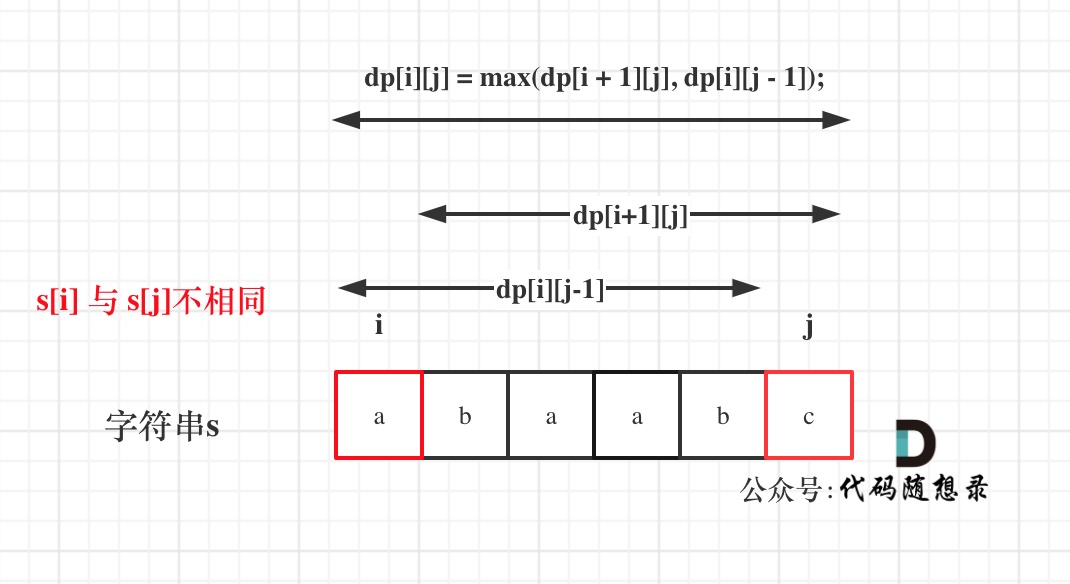
情况2：s[i] != s[j]

首尾字符不同，有两种选择：
1. 去掉 s[i]：dp[i+1][j]
2. 去掉 s[j]：dp[i][j-1]
取两者最大值：dp[i][j] = max(dp[i+1][j], dp[i][j-1])

3. DP数组初始化

i 与 j 相同：dp[i][i] = 1
其他情况dp[i][j]初始为0

4. 确定遍历顺序

从递归公式中，可以看出，dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]。

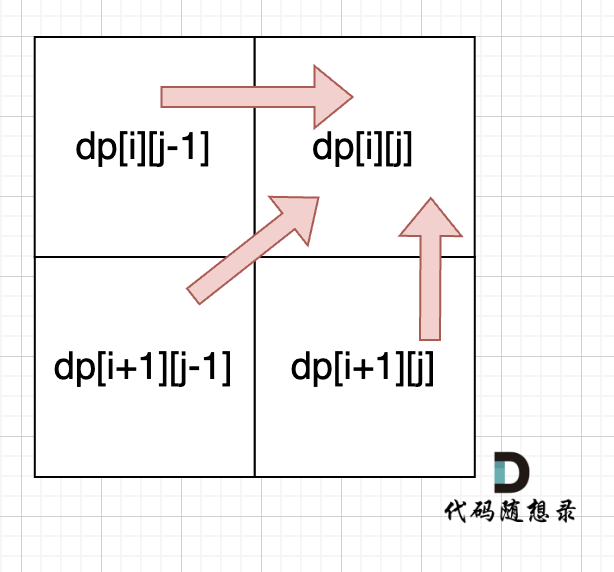
从下到上遍历，从左向右遍历。

5. 打印DP数组

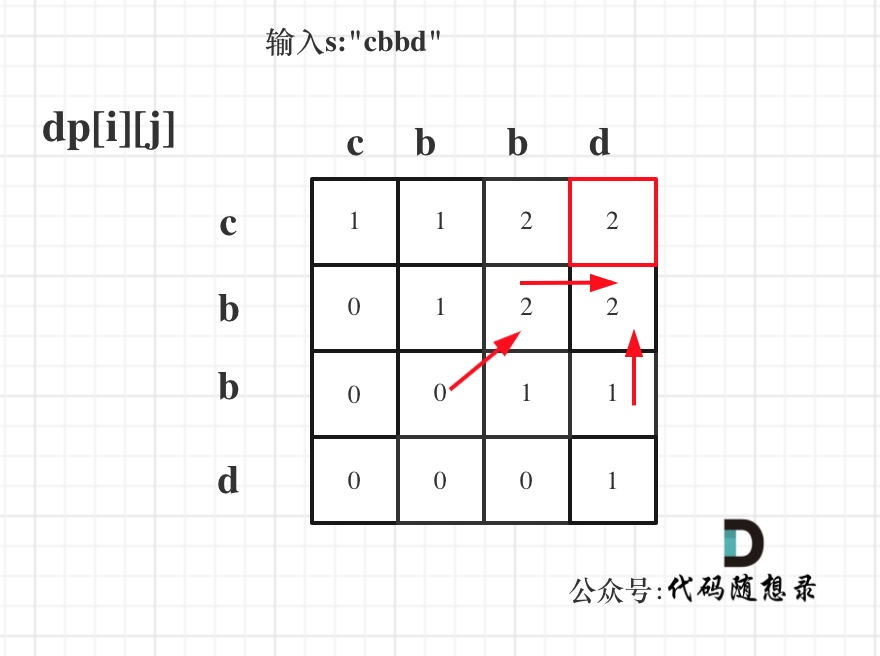
红色框即：dp[0][s.size() - 1]; 为最终结果。

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <sstream>
#include <cmath>
using namespace std;

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        
        int m = s.size();
        vector<vector<int>> dp(m, vector<int>(m, 0));

        for(int i = 0; i < m; i++){
            dp[i][i] = 1;
        }

        for(int i = m - 1; i >= 0; i--){
            for(int j = i + 1; j < m; j++){
                if(s[i] == s[j]){
                    dp[i][j] = dp[i + 1][j - 1] + 2; 
                }else{
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                } 
            }
        }

        for(int i = 0; i < m; i++){
            for(int j = 0; j < m; j++){
                cout << dp[i][j] << " ";
            }
            cout << endl;
        }
        cout << endl;

        return dp[0][m - 1];
    }
};

int main(){

    string s;

    cout << "s: ";
    getline(cin, s);

    Solution obj;
    int res = obj.longestPalindromeSubseq(s);

    cout << "res: " << res << endl;
    
    return 0;
}

s: cbbd
1 1 2 2 
0 1 2 2
0 0 1 1
0 0 0 1

res: 2