查找除了线性表的查找(顺序、二分、分块),树上查找(BST、B-树),还有一种散列查找。
相比于前两种查找,散列表的查找效率惊人的高O(1),它采用的直接寻址技术,基本上就是实现了精准打击,达到一击而中的效果。
所谓的直接寻址技术,说白了,就是存储记录时,通过散列函数计算出一个散列地址;读取记录时,通过同样的散列函数计算出地址,然后按照地址访问记录。整个过程有点类似于数学中的映射,一个或者多个key通过映射对应到一个地址,同样也不会存在多个地址对应一个key的情况。
这里提到了一个关键:散列函数
散列函数,其实就是一种映射关系。它的选取,一般会遵循两个原则:从实现上说要求简单,从效果上说要求均匀。认真想一下就不难明白,我们的散列查找本来就要求高效,如果在这个计算地址的过程山一重水一重,那岂不是南辕北辙了?所以越简单越好。那为什么要求均匀呢?这就涉及到另外一个问题,冲突。不妨先假想一下,如果采用的散列函数计算出来的地址个个都一样,再不做特殊处理的话,取值访问的时候,那不是目瞪口呆无从下手了。
那到底该如何选取所谓的散列函数呢,在前辈们的探索中,总结出来一些具有代表性的方法,这里就直接贴出来了。
散列函数的构造
直接定址
名字听起来很高大上,其实是最简单的。
举个例子来说,现在要统计一下班级同学的年龄分布,我们看一下数据,1990年的有2人,1991年的有8人,1992年的有10人…,1999年的有1人。不难发现,所有的时间(key)都是199开头的,我们存储的时候,完全可以用0,1,2…来表示相应的年份,即f(key) = key -1990。特点:实现简单,但存储前必须了解数据分布。
数字分析
既然能分析的,必然是有规律的,不然再分析也没什么卵用。
看个例子,比如要登记公司的员工信息,用手机号做关键字。我们发现公司员工竟然用的都是形如135XXXX1234的手机号,顺便普及一下,135代表号段,XXXX代表地区识别号,1234才是真正的用户编号。存储的时候,何不用直接用最后四位来表示用户的散列地址呢?特点:实现简单,存储前必须了解数据分布,数据必须有规律。
平方取中
通俗易懂,如名所述。将关键字平方之后,取中间的若干位最为散列地址特点:可以没规律,适合关键字较小的数据
折叠
这个比较特别。
当关键字比较大的时候,平方运算就比较吃力了。这个时候可以考虑折叠。折叠的核心在于将关键字从左到右平均拆成若干份,位数不够的补0,然后把这几部分求和,最后的结果作为散列地址。特点:可以没规律,适合关键字较大的数据
随机数法
比较简单,如名所述。
把关键字当成种子,生成随机数作为散列地址。值得说明的是,这里的随机只是一种伪随机,不然访问数据的时候找不到地址,可就尴尬了。特点:适合关键字长度不等
除数留余
这个应该是用的比较多的。
核心思想一般是选取表长m作为除数,用关键字key除以m,所得的余数作为散列地址。特点:除数的选取至关重要
冲突处理
前面已经说过,不管采用哪种方法构造出来的散列函数,最终生成的散列地址都有可能重复,也就是所谓的冲突,只是概率的大小问题。
当冲突不可避免时,就不得不考虑解决方案了。这里介绍常见的四种。
开放定址法
不知道谁起的名字,简直无语之极。说穿了,就是一旦发生了冲突,就去寻找下一个地址,只要散列表足够大,总能找到适合的地址。这模式,跟丑旦我找女朋友一毛一样,好不容易喜欢上一个姑娘,可人家不愿意,我又不想等,那怎么办,赶紧换下一家呗。用数学的语言描述一下这个过程,就是
fi(key) = (f(key)+di) MOD m (di=1,2,…,m-1) di的选取,可以线性,也可以选择平方或者随机数,来提升均匀性。链地址法
把它俩放一块说,可以比较着来看。还说前面的找女朋友吧,人家不愿意,但是丑旦我脑子被偶像剧安利多了,决定要等等看,说不定女神有一天就能够回眸一笑回心转意,我等啊等,女神没有垂青,我擦嘞反倒是等来了两个情敌…最让我气愤的是,这两个情敌竟然也是个痴情的种子,那咋办嘞?不如组成个联盟,一块等吧。我先来的我是资深备胎,你后来的你是一般备胎,他最后来的他是实习备胎…
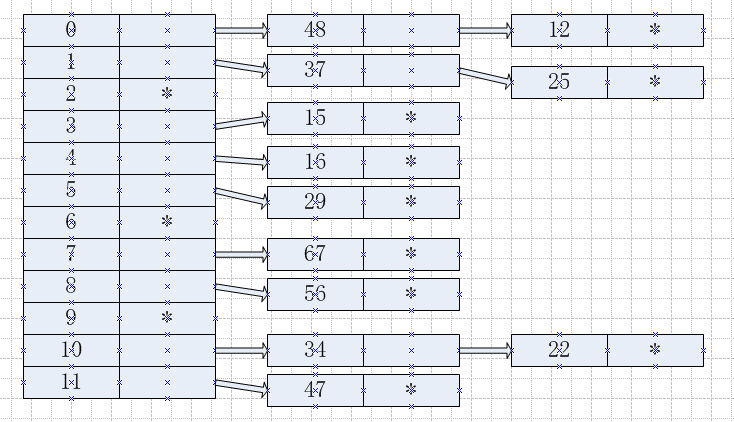
假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},使用除留余数法求散列表。
图片比较丑,但能说明情况,其中*表示初始化的默认值,一般是key不可能取到的值。再哈希
再哈希的核心思想就是,如果一个哈希函数不能保证不重复,那就用两个。经过两个不同的哈希函数计算出来的结果重复的概率就大大降低,所以再哈希的性能是比较好的。用数学语言描述一下就是:
hi=( h(key)+i*h1(key) )%m 0≤i≤m-1 结果显然是由h(key)和h1(key)共同决定的。公共溢出区
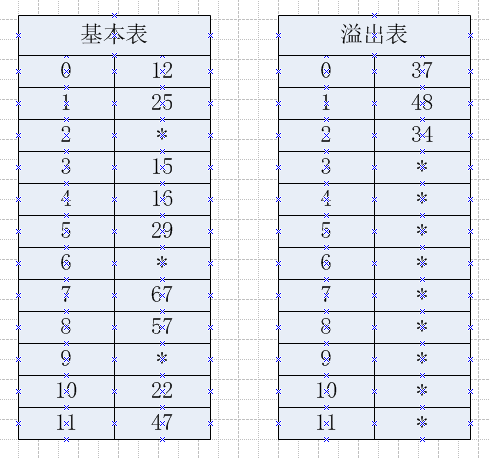
这个就更直白了,开辟两张表:基本表和溢出表,将所有冲突的“情敌”单独存放到溢出表中,可以参考下面的例子。例:假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},同样使用除留余数法求散列表。
依然比较丑,*表示初始化的默认值,一般是key不可能取到的值。
代码实现
下面使用“除数留余”和“开放地址”来模拟一下哈希查找。
要插入的数据是{ 12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34 };
老规矩,能上代码就不多说话。
public class HashSearch {
public static int defaultValue = -1111;
/**
* <p>name: main</p>
* <p>description: </p>
* <p>return: void</p>
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
Hash hash = initTable(12);
int[] array = { 12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34 };
for (int i = 0; i < array.length; i++) {
insert(array[i], hash);
}
for (int i = 0; i < array.length; i++) {
System.out.println("" + search(array[i], hash));
}
}
public static class Hash {
int length;
int[] address;
public Hash(int length) {
this.length = length;
}
}
//初始化
public static Hash initTable(int size) {
Hash hash = new Hash(size);
hash.address = new int[size];
for (int i = 0; i < hash.address.length; i++) {
hash.address[i] = defaultValue;
}
return hash;
}
//计算哈希值
public static int computeHash(int key,Hash hash) {
if (hash.length > 0) {
return key % hash.length;
}
return defaultValue;
}
//插入
public static void insert(int key, Hash hash) {
int index = computeHash(key, hash);
while (hash.address[index] != defaultValue) {// 不是默认值,说明冲突
index = (index + 1) % hash.length;// 开放定址法的线性探测,每次加1,往后寻找
}
hash.address[index] = key;
}
//查找
public static boolean search(int key, Hash hash) {
int index = computeHash(key, hash);
while (hash.address[index] != key) {
index = (index + 1) % hash.length;
/**
* di取值是(0,length-1].
* index==computeHash(key,hash),说明已经加够一个周期了,依然不存在,即可返回;
* hash.address[index] == defaultValue,说明出现了空位依然没有找到key,即可返回.
*/
if (hash.address[index] == defaultValue
|| index == computeHash(key, hash)) {
return false;
}
}
System.out.println("找到" + key + "了,它在表中的第" + index + "个位置");
return true;
}
}
程序的输出:
找到12了,它在表中的第0个位置
true
找到67了,它在表中的第7个位置
true
找到56了,它在表中的第8个位置
true
找到16了,它在表中的第4个位置
true
找到25了,它在表中的第1个位置
true
找到37了,它在表中的第2个位置
true
找到22了,它在表中的第10个位置
true
找到29了,它在表中的第5个位置
true
找到15了,它在表中的第3个位置
true
找到47了,它在表中的第11个位置
true
找到48了,它在表中的第6个位置
true
找到34了,它在表中的第9个位置
true手动计算的结果:

good,两下吻合。
哈希查找就先研究到这里,欢迎留言拍砖嘞。






















 2029
2029

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








