【多任务损失】用不确定度来自适应设定各损失函数的权重

🌔在多任务中，总损失常常是各分任务损失的线性加权，此时各分任务损失的权重设定就显得尤为重要。

比如在JDE算法中就使用了多任务损失的自适应设定：

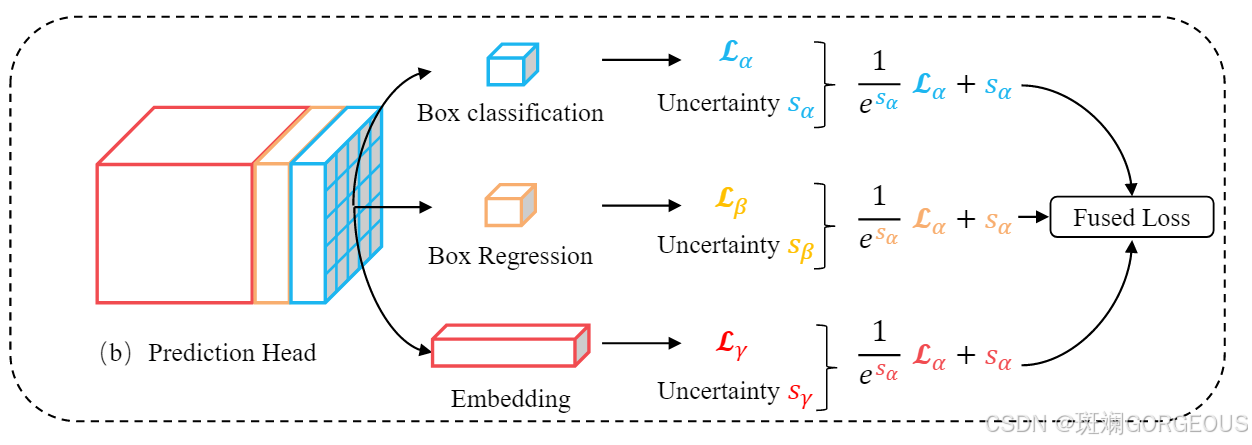
这里使用的权重自适应方法便来自以下这篇文章发掘的不确定度与权重的关系：

Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics

本文正是基于此，用步步衔接的数学推导，讲解多任务损失函数权重设定原理。

总的来说用不确定度估计多任务损失权重的核心是：

各任务的权重与其对应的噪声成反相关

0️⃣ 多任务独立性

⭐️对于模型输出${\mathbf{f}}^{\mathbf{W}}(\mathbf{x})$以及对应的真值$\mathbf{y}$，多任务(假设是相互独立的)的概率估计可以表示为以下这种形式：
$p({\mathbf{y}}_1,\dots ,{\mathbf{y}}_{\mathbf{K}}|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))=p({\mathbf{y}}_1|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))\dots p({\mathbf{y}}_{\mathbf{K}}|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))$
假设使用$-\log$来计算损失，则有：
$$\begin{gathered} L_{total} \\ =-\log [p({\mathbf{y}}_1,\dots ,{\mathbf{y}}_{\mathbf{K}}|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))] \\ =(-\log [p({\mathbf{y}}_1|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))])+\cdots +(-\log [p({\mathbf{y}}_{\mathbf{K}}|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))]) \\ =L_1+\cdots +L_K \end{gathered}$$
因而，基于此就可以使用概率估计来融合各分任务的损失表达。

1️⃣ 连续类损失(回归)

⭐️以回归问题为例，讲解对连续类损失的处理方式。

假设回归问题的概率满足Gaussian分布，依此估计其概率，则有：
$p(y|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(y-f^W(x){)}^2}{2{\sigma }^2}}$
写成损失的形式：
$-\log (y|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma )=\frac{(y-f^W(x){)}^2}{2{\sigma }^2}-\log (\frac{1}{\sqrt{2\pi }\sigma })\approx \frac{\parallel y-f^W(x){\parallel }_2}{2{\sigma }^2}+\log (\sigma )$

2️⃣ 离散类损失(分类)

⭐️以分类问题为例，讲解对离散类损失的处理方式。

使用Softmax对分类输出进行处理，依此估计其概率，其中$\sigma$是一个尺度因子：
$p(\mathbf{y}=c|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma )=Softmax(\mathbf{y},\frac{1}{{\sigma }^2}{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))=\frac{e^{\frac{1}{{\sigma }^2}{f}_c^W(\mathbf{x})}}{{\sum }_{c^{\prime }}{e}^{\frac{1}{{\sigma }^2}{f}_{c^{\prime }}^W(\mathbf{x})}}$
写成损失的形式：
$-\log (p(\mathbf{y}=c|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}),\sigma ))=-\frac{1}{{\sigma }^2}{f}_c^W(\mathbf{x})+\log ({\sum }_{c^{\prime }}{e}^{\frac{1}{{\sigma }^2}{f}_{c^{\prime }}^W(\mathbf{x})})$

3️⃣ 多任务损失组合

⭐️假设有两个任务：回归任务1（连续），分类任务2（离散），则有：
$$\begin{gathered} L(\mathbf{W},{\sigma }_1,{\sigma }_2) \\ =-\log (p({\mathbf{y}}_1,{\mathbf{y}}_2=c|{\mathbf{f}}^{\mathbf{W}}(\mathbf{x}))) \\ =-\log [(\frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(y_1-f^W(x){)}^2}{2{\sigma }_1^2}})\cdot (\frac{e^{\frac{1}{{\sigma }_2^2}{f}_c^W(\mathbf{x})}}{{\sum }_{c^{\prime }}{e}^{\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^W(\mathbf{x})}})] \\ =\frac{\parallel y_1-f^W(x){\parallel }_2}{2{\sigma }_1^2}+\log ({\sigma }_1)-\frac{1}{{\sigma }_2^2}{f}_c^W(\mathbf{x})+\log (\sum _{c^{\prime }}{e}^{\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^W(\mathbf{x})}) \\ =\frac{\parallel y_1-f^W(x){\parallel }_2}{2{\sigma }_1^2}+\log ({\sigma }_1)+[-\frac{1}{{\sigma }_2^2}{f}_c^W(\mathbf{x})+\frac{1}{{\sigma }_2^2}\log (\sum _{c^{\prime }}{e}^{f_{c^{\prime }}^W(x)})]-\frac{1}{{\sigma }_2^2}\log (\sum _{c^{\prime }}{e}^{f_{c^{\prime }}^W(x)})+\log (\sum _{c^{\prime }}{e}^{\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^W(\mathbf{x})}) \\ =\frac{1}{2{\sigma }_1^2}{L}_1(\mathbf{W})+\frac{1}{{\sigma }_2^2}{L}_2(\mathbf{W})+\log ({\sigma }_1)+\log [\frac{{\sum }_{c^{\prime }}{e}^{\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^W(\mathbf{x})}}{({\sum }_{c^{\prime }}{e}^{f_{c^{\prime }}^W(\mathbf{x})}{)}^{\frac{1}{{\sigma }_2^2}}}] \\ \approx \frac{1}{2{\sigma }_1^2}{L}_1(\mathbf{W})+\frac{1}{{\sigma }_2^2}{L}_2(\mathbf{W})+\log ({\sigma }_1)+\log ({\sigma }_2) \end{gathered}$$
其中，
$\{\begin{array}{l}{L}_1(\mathbf{W})=\parallel y_1-f^W(x){\parallel }_2\\ L_2(\mathbf{W})=-\log [Softmax(y_2,f^W(x))]=-\log (\frac{e^{f_c^W(\mathbf{x})}}{{\sum }_{c^{\prime }}{e}^{f_{c^{\prime }}^W(\mathbf{x})}})\\ \frac{1}{{\sigma }_2^2}{\sum }_{c^{\prime }}{e}^{\frac{1}{{\sigma }_2^2}{f}_{c^{\prime }}^W(x)}\approx ({\sum }_{c^{\prime }}{e}^{f_{c^{\prime }}^W(\mathbf{x})}{)}^{\frac{1}{{\sigma }_2^2}}\end{array}$

4️⃣ 实际操作中的近似处理

⭐️最后，在实际操作中，通过预测$s:=\log ({\sigma }^2)$来代替预测${\sigma }^2$，因为这样在数值上更加稳定，而且没有除0等问题，则最后多任务损失可以近似写成：
$L(\mathbf{W},s_1,s_2)=\frac{1}{e^{s_1}}{L}_1(\mathbf{W})+\frac{1}{e^{s_2}}{L}_2(\mathbf{W})+s_1+s_2$