装配线问题:
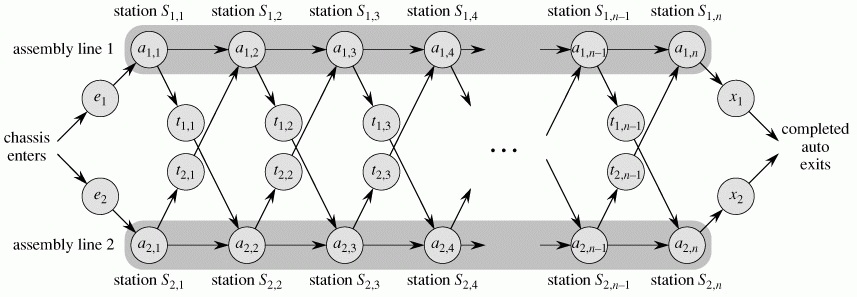
某个工厂生产一种产品,有两种装配线选择,每条装配线都有n个装配站。可以单独用,装配线1或2加工生产,也可以使用装配线i的第j个装配站后,进入另一个装配线的第j+1个装配站继续生产。现想找出通过工厂装配线的最快方法。
装配线i的第j个装配站表示为
Si,j
,在该站的装配时间是
ai,j
如果从
Si,j
装配站生产后,转移到另一个生产线继续生产所耗费的时间为
ti,j
进入装配线花费时间
ei
,完成生产后离开装配线所耗费时间为
xi
令f*表示通过生产所有路线中的最快的时间
令
fi[j]
表示从入口到装配站
Si,j
的最快的时间.(i=1,2 ; j=1,2,…n;)
f1[1]
=
e1
+
a1,1
f2[1]
=
e2
+
a2,1
通过装配站 S1,j 的最快路线可能是通过 S1,j−1 站直接到 S1,j ,也可能是通过 S2,j−1 站,从装配线2到装配线1.
所以
f1[j]
= min(
f1[j−1
] +
a1,j
,
f2[j−1
] +
t2,j−1
+
a1,j
) (j=2,3…n)
同理
f2[j]
= min(
f2[j−1
] +
a2,j
,
f1[j−1
] +
t1,j−1
+
a2,j
) (j=2,3…n)
所以有递归公式:
动态规划思想
采用动态规划的前提:具有最优子结构和重叠子问题的性质。
在求解
f1[n]
和
f2[n]
的过程中,需要求解
f1[n−1]
和
f2[n−1]
,继续向前迭代计算…
即需要计算所有出所有的
fi[j]
,,i=0,1;j=1,2…n,此过程中需要不断的对同一个问题进行多次计算。
例如
f1[n]
的次数
r1[n]
为1,那么
r1[n−1]
=
r1[n]
+
r2[n]
,
r1[n−2]
=
r1[n−1]
+
r2[n−1]
,呈现指数增长,即
ri[j]=2n−j
;
由上问题满足重叠的子问题的性质,
构成原问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解,即满足最优子结构。
动态规划的思想即安排求解顺序,对每个子问题只求解一次,并将结果保存下来,如果随后再次需要求此问题的解,只需要查找保存的结果,而不必重新计算
因为 fi[j] 的值是由 f1[j−1] 和 f2[j−1] 决定,所以采用递增的站编号来计算 fi[j] ,自底向上的方法。
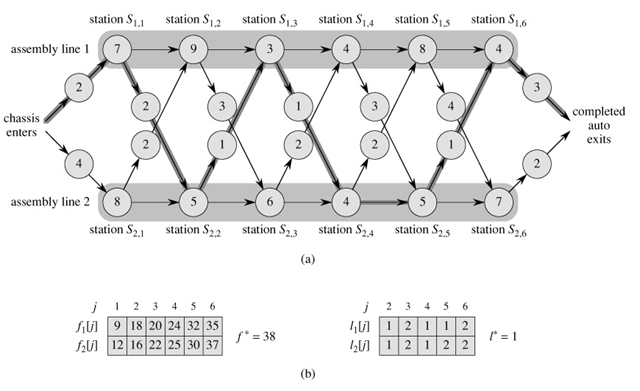
例程
:
颜色深的线表示最快的装配路线
其中
li[j]
,表示,到达装配线i的第j个装配站的最快路线的位置,值为1或2。
l*表示产品最后出自哪个装配线值为1或2
/************************************************************************/
/*
CSDN 勿在浮沙筑高台
http://blog.csdn.net/luoshixian099
算法导论--动态规划
2015年6月1日 */
/************************************************************************/
#include <stdio.h>
int f[2][6]={0}; //对应通过各个装配站的最短时间
int l[2][6]={0}; //对应通过各个装配站的来源
int __L;
int __F;
void Fastest_Way(int a[][6],int t[][5],int e[],int x[],int n)
{
int j=0;
f[0][0] = e[0]+ a[0][0];
f[1][0] = e[1]+ a[1][0];
for (j=1;j<n;j++) //自底向上开始计算f[i][j]的值,与l[i][j]的值
{
if (f[0][j-1]+a[0][j] <= f[1][j-1]+t[1][j-1]+a[0][j])
{
f[0][j] = f[0][j-1]+a[0][j];
l[0][j] = 0;
}
else
{
f[0][j] = f[1][j-1]+t[1][j-1]+a[0][j];
l[0][j] = 1;
}
if (f[1][j-1]+a[1][j] <= f[0][j-1]+t[0][j-1]+a[1][j])
{
f[1][j] = f[1][j-1]+a[1][j];
l[1][j] = 1;
}
else
{
f[1][j] = f[0][j-1]+t[0][j-1]+a[1][j];
l[1][j] = 0;
}
}
if (f[0][5] + x[0] <= f[1][5] + x[1])
{
__F = f[0][5]+x[0]; // __F为通过装配线的最短时间 __L为产品最后出自哪个生产线
__L = 0;
}
else
{
__F = f[1][5]+x[1];
__L = 1;
}
}
void Print_Station(int l[][6],int __L,int n)
{
/***********逆序输出**************************/
/* int j;
int i = __L;
printf("line %d , station %d\n",i+1,n);
for(j=n-1;j>=1;j--)
{
i = l[i][j];
printf("line %d , station %d\n",i+1,j);
}*/
/***********正序递归输出****************/
if ( n==0 )
return;
__L = l[__L][n];
Print_Station(l,__L,n-1);
printf("line %d , station %d\n",l[__L][n]+1,n);
}
void main()
{
int a[2][6]={{7,9,3,4,8,4},
{8,5,6,4,5,7}};
int t[2][5]={{2,3,1,3,4},
{2,1,2,2,1}};
int x[2]={3,2};
int e[2]={2,4};
Fastest_Way(a,t,e,x,6);
Print_Station(l,__L,6);
}









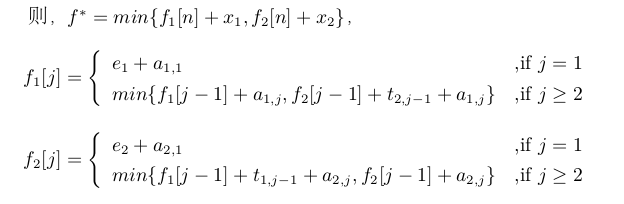














 4105
4105











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








