解方程组的列主元高斯消元法和Cholesky分解
计算数学与科学工程计算研究所 陆嵩
基本思想
一般的高斯消元法的运算量为
O(n3)
,这是我们所不能接受的。高斯消元法本质上就是矩阵的
LU
分解,高斯消元的过程,其实蕴含着求解
L−1b
的过程。如何矩阵的所有顺序主子式都不为零,那么
LU
分解是存在且唯一的,那么正定矩阵一定可进行这个分解。普通的高斯消元方法,引起的误差比较大,为了避免比较小的数做分母,我们可以改为列主元素的高斯消元法。列选主元免去很多元素之间比较的运算,且数值稳定性比较好。
LDLT 分解和Cholesky分解说的是同一个事情,对于正定矩阵,Cholesky分解是存在且唯一的。所以说,矩阵的条件越好,我们可用的工具也就越高端。分解的运算量也是立方量级的,但是它的运算量仅仅为高斯消元法的一半。
当解大量系数矩阵相同而右端项不同的多个方程组时, LU 分解和 LDLT 分解可节省工作量,所以在做列主元高斯消元时,我们应该想办法将上下三角矩阵存起来。
操作步骤
所谓的高斯消元,就是周知的做行变换,将下三角变成零。列主元,是在每一列消元的过程中,将这列中模最大的数挪到对角线上,在做消元。高斯消元的本质就是 LU 分解。Cholesky分解,可以通过待定参数方法,按一列一列的顺序将未知参数求出。事实上, GGT 的第i行第j列元素,就是G的第i行和第j行做内积得到的结果。
实验和结果
简单的c程序
高斯消元法
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
//#include <conio.h>
//*****************************************//
//这个程序摘自蒋长锦书,整体看来还是不错的。有一个可以优化的地方是,他没有把
//A = LU 的 L和U存下来,那么在处理Ax = bi,大量只有右端项的问题时,无疑增加了工作量。
//内存使用合理。
#define DIM 5
#ifndef EPSILON
#define EPSILON 0.000000001
#endif
int gcpelim(int process, double A[DIM][DIM], double xx[DIM]);
int main(int argc, char** argv) {
int i;
static double A[DIM][DIM] = {
{ 2.0, -1.0, 4.0, -3.0, 1.0 },
{ -1.0, 1.0, 2.0, 1.0, 3.0 },
{ 4.0, 2.0, 3.0, 3.0, -1.0 },
{ -3.0, 1.0, 3.0, 2.0, 4.0 },
{ 1.0, 3.0, 1.0, 4.0, 4.0 }
};
static double b[DIM] = { 11.0, 14.0, 4.0, 16.0, 18.0 };
system("cls");
//定义了静态变量A和b,所谓静态变量就是不可被修改。
if (gcpelim(0, A, b) == 1) {
printf("The linear system hasn't solution!\n");
printf("Strike any key to exit!\n");
getchar();
exit(1);//退出程序
}
printf("\nthe solution of Column principle elimination :\n");
for (i = 0; i < DIM; i++) {
printf("%10.6f\n", b[i]);
}
//按一定的精度输出b。
printf("\n\n Press any key to exit.\n");
getch();
}
int gcpelim(int process, double A[DIM][DIM], double xx[DIM]) {
int k, i, j, i0;
printf("A = \n");
for (i = 0; i < DIM; i++) {
for (j = 0; j < DIM; j++) {
printf("%12.8f", A[i][j]);//打印A
}
printf("\n");
}
printf("b = \n");
for (i = 0; i < DIM; i++) {
printf("%12.8f", xx[i]);
printf("\n");
}
double pelement;
if (process == 1) printf("The process of elimination\n");
for (k = 0; k < DIM; k++) {
pelement = fabs(A[k][k]);//给对角线去绝对值,赋值给pelement
i0 = k;
for (i = k; i<DIM; i++) {
if (fabs(A[i][k] > pelement)) {
pelement = fabs(A[i][k]);//找每一列元素绝对值最大值,赋值给pelement,这步看似有点多余
i0 = i;//标记最大元素所在的行
}
}
if (i0 != k) {//若最大值不在对角线上 ,则交换两列
for (j = 0; j < DIM; j++) {
pelement = A[k][j];
A[k][j] = A[i0][j];
A[i0][j] = pelement;
}//这个程序有个小缺点就是没有把交换的过程存下来,这样当处理仅右端项b不同的一系列方程组时,增加了工作量
pelement = xx[k];
xx[k] = xx[i0];
xx[i0] = pelement;//b值也交换
}
if (process == 1) {//标志位控制是否打印过程
for (i = 0; i < DIM; i++) {
for (j = 0; j < DIM; j++) {
printf("%10.6f", A[i][j]);
}
printf(" | %10.6f\n", xx[i]);
}
printf("\n");
}
if (fabs(A[k][k]) < EPSILON) {
return(1);
}
for (i = k + 1; i < DIM; i++) {
A[i][k] = A[i][k] / A[k][k];//求一个倍数
for (j = k + 1; j < DIM; j++) {//为了节省内存,将左下角变零的部分该存了消元的倍数,右上三角是消元后的结果
A[i][j] = A[i][j] - A[i][k] * A[k][j];
}
//A的左下角就是LU分解(PA = LU)中的L(对角线补充1),右上角就是U,LU分解并不是唯一的,但是求解的结果唯一。
xx[i] = xx[i] - A[i][k] * xx[k];
}
if (process == 1) {
for (i = 0; i < DIM; i++) {
for (j = 0; j < DIM; j++) {
printf("%10.6f", A[i][j]);
}
printf(" | %10.6f\n", xx[i]);
}
printf("\n");
}
}
for (i = DIM - 1; i >= 0; i--) {//最后求解右上三角方程
for (j = i + 1; j < DIM; j++) {
xx[i] = xx[i] - A[i][j] * xx[j];
}
xx[i] = xx[i] / A[i][i];
}
return (0);
}
Cholesky分解
//库调用
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
//#include <conio.h>
//宏定义
#ifndef EPSILON
#define EPSILON 0.000000001//设置默认精度
#endif
#define DIM 4
//函数声明
int chollt(double A[DIM][DIM]);
int trillt(double A[DIM][DIM], double x[DIM]);
void main()
{
int i, j;
static double A[DIM][DIM] = {
{ 5.5, 7.0, 6.0, 5.5 },
{ 7.0, 10.5, 8.0, 7.0 },
{ 6.0, 8.0, 10.5, 9.0 },
{ 5.5, 7.0, 9.0, 10.5 } };//初始化静态矩阵A
static double b[DIM] = { 23.0, 32.0, 33.0, 31.0 };//初始化b
system("cls");//清屏
printf("要求解的方程组为:\n A ||| b\n");
for (i = 0; i < DIM; i++)
{
for (j = 0; j < DIM; j++)
{
printf("%f ", A[i][j]);
}
printf("||| %f\n", b[i]);
}
if (chollt(A) == 1)
{
printf("Matrix isn't a positive define!\n");
printf("Strike any key to exit!\n");
getch();
exit(1);
}
printf("\nCholesky decomposition:\n");
for (i = 0; i < DIM; i++)
{
for (j = 0; j <= i; j++)
{
printf("%12.8f", A[i][j]);//打印分解后的值
}
printf("\n");
}
printf("\n");
if (trillt(A, b) == 1)
{
printf("The system hasn't solution! Strike any key to exit!");
getch();
exit(1);//无解退出程序
}
printf("The solution is:\n");
for (i = 0; i < DIM; i++)
{
printf("%12.7f\n", b[i]);
}
printf("\nPress any key to exit!\n");
getch();
}
int chollt(double A[DIM][DIM])//cholesky分解函数定义,输入A
{
int i, j, k;
for (k = 0; k < DIM; k++)
{
for (i = k; i < DIM; i++)
{
for (j = 0; j < k; j++)
{
A[i][k] = A[i][k] - A[i][j] * A[k][j]; //这里没有给三角矩阵再开辟内存,而是直接存在了原来的A中,节省了很大内存。
}
}
if (fabs(A[k][k]) < EPSILON)//如果分解出的矩阵对角元出现了非正值,即特征值有非正值,那么矩阵就不是正定的。
{
printf("%f", A[k][k]);
return 1;
}
A[k][k] = sqrt(A[k][k]);//一列的对角元先处理,同一列其余的部分后面处理
for (i = k + 1; i < DIM; i++)
{
A[i][k] = A[i][k] / A[k][k];//除对角线元素最后来处理
}
}
return 0;
}
int trillt(double A[DIM][DIM], double x[DIM])//简单的下三角矩阵的求解
{
int i, j;
for (i = 0; i < DIM; i++)
{
for (j = 0; j < i; j++)
{
x[i] = x[i] - A[i][j] * x[j];
}
if (fabs(A[i][i]) < EPSILON) //下三角奇异,无解
{
return 1;
}
else
{
x[i] = x[i] / A[i][i];
}
}
for (i = DIM - 1; i >= 0; i--)
{
for (j = i + 1; j < DIM; j++)
{
x[i] = x[i] - A[j][i] * x[j];
}
x[i] = x[i] / A[i][i];
}
return 0;
}
实验结果
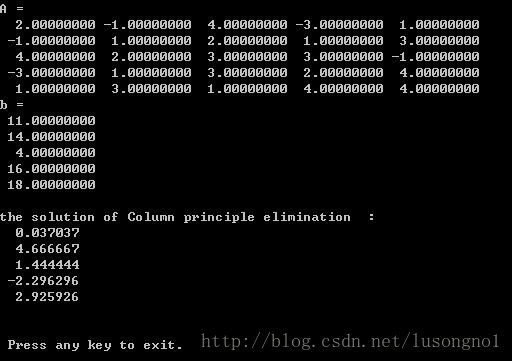
{width=”16cm”}\
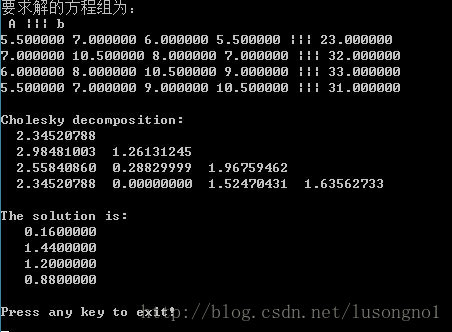
{width=”16cm”}\


























 4182
4182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










