测量不确定度

一、测量不确定度来源

    任何测量值都不是绝对准确的，最初使用误差来衡量 测量值与真值之间的差异。

           误差=随机误差+系统误差，

由于各种因素的存在，每次测量时 测量值与真值之间的差异应该有所同，但会介于一定范围内。误差值是个点值不能准确的表达测量值与真值之间的差异，基于逻辑和准确性考虑，使用测量不确定度。

二、测量不确定度

2.1 测量不确定度：

表征合理地赋予被测量之值的分散性，与测量结果相联系的参数。

1. 测量不确定度是个范围；

2）有多 少个来源就有多少个不确定度。

2.2 方差合成定理是测量不确定度的基础：

  1) 若一个随机变量是两个或多个独立随机变量之和，则该随机变量的方差等于各分量的方差之和

    V(y)= V(x1)+ V(x2)+…+V(xn)

根据标准不确定度的定义，方差即是标准不确定度的平方

    u2(y)= u2(x1)+ u2(x2)+…+u2(xn)

2)  若y=c1x1+c2x2+…+cnxn

根据方差的性质：随机变量与常数之乘积的方差，等于随机变量的方差与该常数的平方之乘积

 

三、不确定度评定步骤

3.1  不确定度评定步骤

）寻找不确定度来源

）建立满足测量不确定度评定所需的数学模型

）确定对应于各输入量的标准不确定度分量ui(y)

）确定对应于各输入量的标准不确定度分量ui(y)

）列出不确定度分量汇总表

）将各标准不确定度分量ui(y)合成得到合成标准不确定度uc(y)

）确定被测量Y可能值分布的包含因子

）确定扩展不确定度

）给出测量不确定度报告

3.2 建立数学模型

3.2.1 步骤二中建立数学模型的方法有

     1）透明箱模型：对测量原理了解比较透彻时，即每个输入量对被测量的影响方式一清二楚，且其影响的大小可以根据数学表达式定量地进行计算，数学模型可以从测量的基本原理直接得到

     2）黑箱模型：在很多情况下，有许多输入量对测量结果的影响是无法用解析形式的数学表达式表示的，只能根据经验估计输入量对测量结果的影响，这时，就可以采用增加一个修正项的方式将其补充到数学模型中，即采用黑箱模型的方式。

3.2.2 数学模型通式：

测量结果＝真值＋误差＝真值＋系统误差＋随机误差

真值＝测量结果＋系统误差的修正值＋随机误差的修正值

则数学模型的通式为：

被测量等于测量结果的计算公式加上由于系统误差所引入的修正值（即数学期望不等于零的修正值），再加上由于随机误差所引入的修正值（即数学期望等于零的修正值）。

3.3 各输入量估计值xi的标准不确定度u(xi)评定

      评定方法分为A类和B类：

3.3.1 A类（A类评定的标准不确定度仅来源于对具体测量结果的统计评定）

(1)基本方法：贝塞尔法

•a）若在重复性条件下对被测量X作n次独立重复测量，测量的结果为。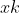 

用标准偏差表示的不确定度称为标准不确定度，则单次测量结果的标准不确定度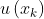

为

b) 若采用该n次测量结果的平均值作为测量结果的最佳估计值

平均值

,

则平均值的实验标准差为

 

注意：当测量次数n较小时，计算得到的实验室标准差可能会有较大的误差 ，所以，使用贝塞尔法时要求n应较大，一般要求≥10。

c) 若所给测量结果是m次（m可以比较小）重复测量的平均值

(2)合并样本标准差:

•a)  若在重复性条件下对被测量X作n次独立观测，并且有m组这样的测量结果，各组间的测量条件可能会稍有不同，就不能直接采用贝塞尔公式，可以考虑采用合并样本标准差。

b)  若已计算出m组测量结果的实验标准差sj(xk),且每组包含的测量次数相同，则合并样本标准差

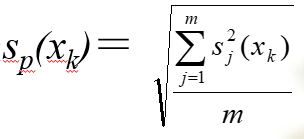
 则可以看出：合并样本标准差并不是各组的实验标准差的平均值，而是采用方差的平均。

•各组包含的测量次数不完全相同，则合并样本标准差为：

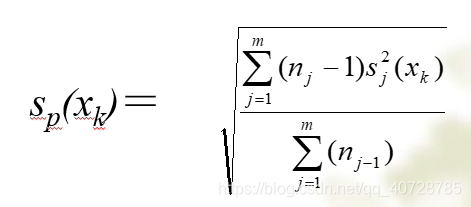
•c)  若最后给出的测量结果是若干次（N）测量结果的平均值

(3) 极差法（适用于测量次数少）

  可以估计被测量X接近正态分布的前提下，单次测量结果xk的实验标准差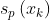近似评定：

 

(4)最小二乘法

•估计值x和y之间有线性关系y=a+bx；同时假定x的测量不确定度远小于y的测量不确定度，则可采用最小二乘法得到参数a、b及它们的标准不确定度u(a)、u(b)

•写出y=a+bx的误差方程，分别对a和b求偏导，同时使偏导数为0，可得联立方程，求得a和b。

•对x测量，得值x0,通过计算的a和b,得y0,可以计算出的标准不确定度u(y0)

•对y重复测量p次，得y的平均值y0,通过计算的a和b,得x0,可以计算出的标准不确定度u(x0)

•最小二乘法常用于测量仪器作校准曲线

3.3.2  B类（来源于为各种标准和规程等技术性文件、生产部门提供的技术文件、测量人员对仪器特征的了解经验等。）

•信息来源于检定证书或校准证书： 

         (1)给出被测量x的扩展不确定度U(x)和包含因子k:

         (2)给出被测量x的扩展不确定度Up(x)和其对应的置信区间 p:

             大部分情况下会选择正态分布，在不同分布中正态分布的包含因子k最大，得到的标准不确定度就最小。

•信息来源于其他各种资料或手册

 a：输入量x的可能值分布区间的半宽，可以看作它所对应的置信区间的置信概率p＝100％，则实际上它就是该输入量的扩展不确定度。

3.4 合成标准不确定度

下标c表示合成之意，即uc(y)表示被测量Y的合成标准不确定度。

 注：此时各输入量相互独立的或各输入量间相关性可以忽略

 注：此时各输入量相互独立的或各输入量间相关性可以忽略

 3.5 扩展不确定度

扩展不确定度U等于合成标准不确定度uc与包含因子k的乘积。

4.测量不确定度对合格或不合格判定的影响

 

只有当测量结果处于被扩展不确定度 U 扩大了的规范区之外时，即测量结果的完整表述全部处于规范区外时，才能判定产品不合格；同样只有当测量结果处于被扩展不确定度 U 缩小了的规范区之内时，即测量结果的完整表述全部处于规范区内时，才能判定产品合格。

5.检测实验室的能力验证试验

v 在检测实验室的比对中，一般用中位值代替平均值作为参考值。

v 各实验室之间测量结果标准偏差会受到离群值的影响，这种情况通常用四分位数间距 IQR 来代替标准偏差，通过对标准化正态分布进行计算得到正态分布的四分位数间距与标准偏差的比值为 1.3490

v 标准 IQR ＝ IQR/1.3490=0.7341×IQR

v 由于中位值相当于平均值，在比对中就作为参考值，而标准 IQR 相当于标准偏差，则 Z 比分数的最大允许值相当于包含因子 k ，因此对各参加实验室所得到的 Z 比分数的要求为：

v当∣Z∣≤2,由于该结果在95％置信区间内，该结果为满意。

v当2<∣Z∣<3,由于测量结果出现在该区间的概率较小，仅为5％左右，因此该结果为可疑结果，或称有问题结果。

v当∣Z∣≥3，该结果出现的概率不到1％，为小概率事件，故认为该结果为不满意结果，或成为离群结果。

vZ比分数的符号表明测量结果偏离的方向，Z>0表示测量结果大于中位值，Z<0表示测量结果小于中位值。