凸包 —— 五种解法

最新推荐文章于 2022-05-06 10:20:14 发布

lxt_Lucia

最新推荐文章于 2022-05-06 10:20:14 发布

阅读量6.7k

点赞数 29

分类专栏： algorithm knowledge 文章标签：凸包

knowledge 同时被 2 个专栏收录

42 篇文章 22 订阅

订阅专栏

algorithm

26 篇文章 27 订阅

订阅专栏

欢迎访问https://blog.csdn.net/lxt_Lucia～～

宇宙第一小仙女\(^o^)/～～萌量爆表求带飞=≡Σ((( つ^o^)つ~ dalao们点个关注呗～～

关于凸包，之前一直漏掉了这一个，上周末组队赛，听说有一题就是凸包的模板，可惜不会，听说不算很难，正好这周空余的课很少，就顺便搞了8...

1）可以形象地想成这样：在地上放置一些不可移动的木桩，用一根绳子把他们尽量紧地圈起来，这就是凸包了。
2）假设平面上有p0~p12共13个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，我们就叫它“凸包”。如下图：

è¿éåå¾çæè¿°

然后，什么是凸包问题？

一组平面上的点，求一个包含所有点的最小的凸多边形，这就是凸包问题了。
我们把这些点放在二维坐标系里面，那么每个点都能用 (x,y) 来表示。现给出点的数目13，和各个点的坐标，求构成凸包的点。

然后，什么是极角排序和左转判定？

1）极角排序：就是选取一个最左的点，按y最小，其次x最小来定义，接下来所有的点针对该点的射线，按角度由小到大，若相同

按距离由近到远来排序。

2）左转判定：这个和叉积有关，对于向量p1(x1,y1),p2(x2,y2)如果x1*y2-x2*y1>0,则从p1到p2左转

下面，我们来看一下解决凸包问题的五种方法。

解一：穷举法（蛮力法）

时间复杂度：O(n³）。
思路：两点确定一条直线，如果剩余的其它点都在这条直线的同一侧，则这两个点是凸包上的点，否则就不是。
步骤：

将点集里面的所有点两两配对，组成 n(n-1)/2 条直线。
对于每条直线，再检查剩余的 (n-2) 个点是否在直线的同一侧。
如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢？（坐标：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）

è¿éåå¾çæè¿°
当上式结果为正时，p3在直线 p1p2 的左侧；当结果为负时，p3在直线 p1p2 的右边。

解二：分治法

时间复杂度：O(n㏒n)。
思路：应用分治法思想，把一个大问题分成几个结构相同的子问题，把子问题再分成几个更小的子问题……。然后我们就能用递归的方法，分别求这些子问题的解。最后把每个子问题的解“组装”成原来大问题的解。
步骤：

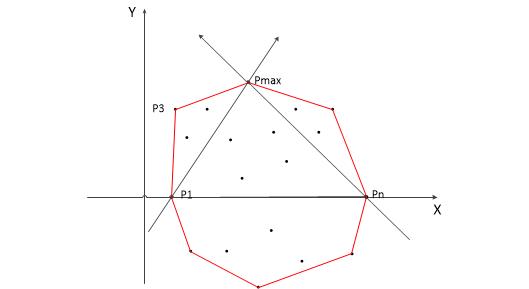
把所有的点都放在二维坐标系里面。那么横坐标最小和最大的两个点 P1 和 Pn 一定是凸包上的点（为什么呢？用反证法很容易证明，这里不详讲）。直线 P1Pn 把点集分成了两部分，即 X 轴上面和下面两部分，分别叫做上包和下包。
对上包：求距离直线 P1Pn 最远的点，即下图中的点 Pmax 。
作直线 P1Pmax 、PnPmax，把直线 P1Pmax 左侧的点当成是上包，把直线 PnPmax 右侧的点也当成是上包。
重复步骤 2、3。
对下包也作类似操作。

è¿éåå¾çæè¿°

然而怎么求距离某直线最远的点呢？我们还是用到解一中的公式：
è¿éåå¾çæè¿°
设有一个点 P3 和直线 P1P2 。（坐标：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）
对上式的结果取绝对值，绝对值越大，则距离直线越远。

注意：在步骤一，如果横坐标最小的点不止一个，那么这几个点都是凸包上的点，此时上包和下包的划分就有点不同了，需要注意。

解三：Jarvis步进法

时间复杂度：O(nH)。（其中 n 是点的总个数，H 是凸包上的点的个数）
思路：

纵坐标最小的那个点一定是凸包上的点，例如图上的 P0。
从 P0 开始，按逆时针的方向，逐个找凸包上的点，每前进一步找到一个点，所以叫作步进法。
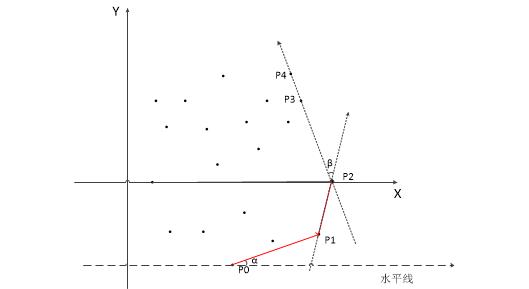
怎么找下一个点呢？利用夹角。假设现在已经找到 {P0，P1，P2} 了，要找下一个点：剩下的点分别和 P2 组成向量，设这个向量与向量P1P2的夹角为 β 。当 β 最小时就是所要求的下一个点了，此处为 P3 。

è¿éåå¾çæè¿°
注意：

找第二个点 P1 时，因为已经找到的只有 P0 一个点，所以向量只能和水平线作夹角 α，当 α 最小时求得第二个点。
共线情况：如果直线 P2P3 上还有一个点 P4，即三个点共线，此时由向量P2P3 和向量P2P4 产生的两个 β 是相同的。我们应该把 P3、P4 都当做凸包上的点，并且把距离 P2 最远的那个点（即图中的P4）作为最后搜索到的点，继续找它的下一个连接点。

解四：Graham扫描法

时间复杂度：O(n㏒n)
思路：Graham扫描的思想和Jarris步进法类似，也是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，但它不是利用夹角。
è¿éåå¾çæè¿°
步骤：

把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
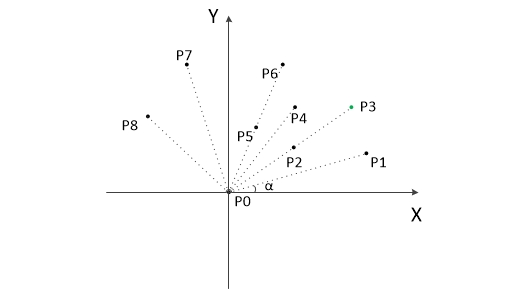
把所有点的坐标平移一下，使 P0 作为原点，如上图。
计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
（以上是准备步骤，以下开始求凸包）
以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：
连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
当前点是凸包上的点，把它压入栈，执行步骤7。
检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。
最后，栈中的元素就是凸包上的点了。

如果没看懂的话，咱们再换种描述方式：

（1）选取最下左的点P0。

（2）计算出每个点相对于P0的角度和距离(利用这个来排序)排序。

（3）设点数为n，将p[n-1]和p[0]入栈，判断点集合是否为一条直线（初始k=2表示当前凸包的大小）。

（4）i 从1到 n-1 遍历，对于p[k-1],p[k-2],p[i]若满足左转，将p[i]压入栈。否则就 i-- ，k-- 。

（5）k-- ，返回k表示凸包的点数。

如果还没懂，那咱们放在动图里看一下。

以下为用Graham扫描法动态求解的过程：

è¿éåå¾çæè¿°

模板代码实现：

int Polygon::Graham(Polygon &con) //别用自己做对象
{
    int t=0,k=0;
    Point tmp;//先y最小再x最小
    for(i=1; i<n; i++)
        if(p[i]<p[t])
            t=i;
    swap(p[t],p[0]);
    for(int i=0; i<n; i++)
    {
        tmp=p[i]-p[0];
        p[i].dis=tmp.Len2();
        p[i].angle=atan2(tmp.y,tmp.x);
    }
    sort(p,p+n,_cmp);
    con.p[k++]=p[n-1];
    con.p[k++]=p[0];
    if(Sig(p[1].angle-p[n-1].angle)==0)
        con.p[k++]=p[n-1];//凸包为一线段
    else
    {
        for(int i=1; i<n; i++)
        {
            if(Sig(Cross(con.p[k-1],con.p[k-2],p[i]))>0)
                con.p[k++]=p[i];
            else
            {
                i--;
                k--;
            }
        }
    }
    return con.n=--k;
}  
/*
9
1 4
3 6
5 7
2 2
3 3
5 4
8 3
9 6
7 1
*/

解五：Melkman算法

è¿éåå¾çæè¿°

说真的，这个算法网上的资料也少的可怜，先把网上的解释截个图在这里。

下面详细介绍一下这个基于Graham扫描线算法却更加强大的凸包算法 —— Melkman算法

为了学习这个新算法，你需要如下前置技能：
1），会计算几何基础，尤其是叉积
2），掌握Graham扫描线算法求凸包
如果你不会如上前置技能，网上各路神犇的关于此的讲解很多，如果能够先点亮这些前置技能，理解这篇博客无疑会更加轻松

那么，如果现在你们已经点亮了上述前置技能……
我们开始吧！！！
对于点集求凸包，Graham扫描线是可以在O（nlogn）的时间内完美解决的，而且很容易可以知道点集求凸包的时间复杂度下界是O（nlogn）。
但是，如果是求简单多边形的凸包呢？（简单多边形：没有自交边的多边形即为简单多边形（凸多边形，凹多边形皆可））。

问题：
平面上有一个简单多边形，沿着多边形的边，按照逆时针的顺序给出多边形的顶点的坐标，要求你求出此多边形的凸包。

如果你还记得对于点集的凸包我们是如何解决的的话，我们先是将点按照某种顺序排序（水平序或极角序），再从某个一定在凸包上的点上的开始扫描。
但是我们注意到，对于按顺序给出的简单多边形上的点，他们本身就带着一个序！！！（感性理解一下）
因此，我们求简单多边形的凸包，只需要从某个必在凸包上的点开始用Graham扫描线计算一圈，就可以求出此多边形的凸包了。。。。。
看起来是这样，其实并不是
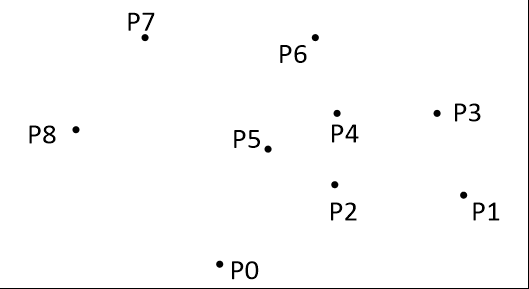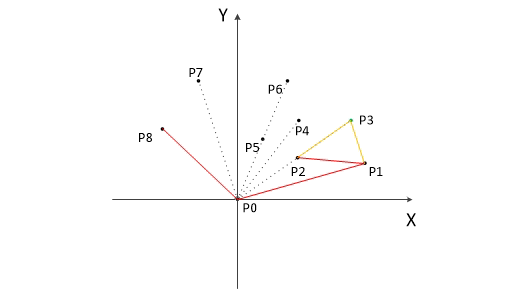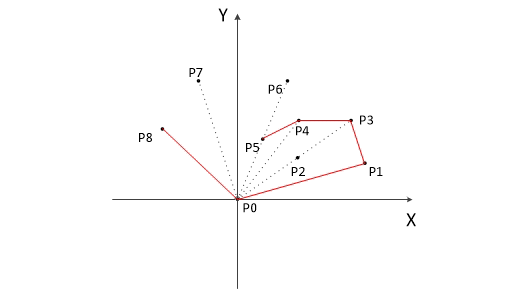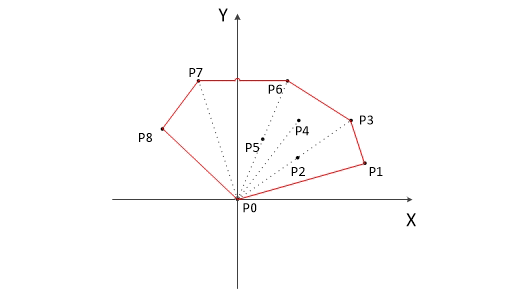
因为Graham 无法处理如下图的简单多边形！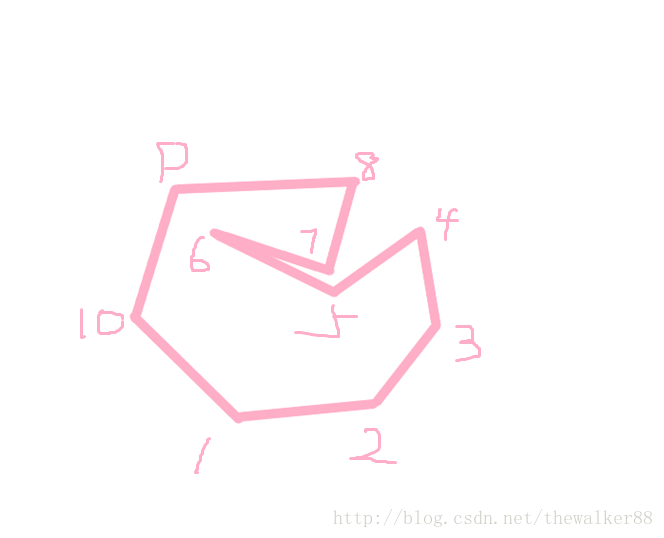

对于这个多边形，我们从一号顶点开始扫描，从1一直到6都是没有问题的，此时栈里面从底到顶的顶点编号是1、2、3、4、6
此时考虑点7，我们惊讶的发现，线段46到线段67是逆时针旋转的，这意味着点7不会造成弹栈 ，最后，我们求出的凸包将是，下图中的红色部分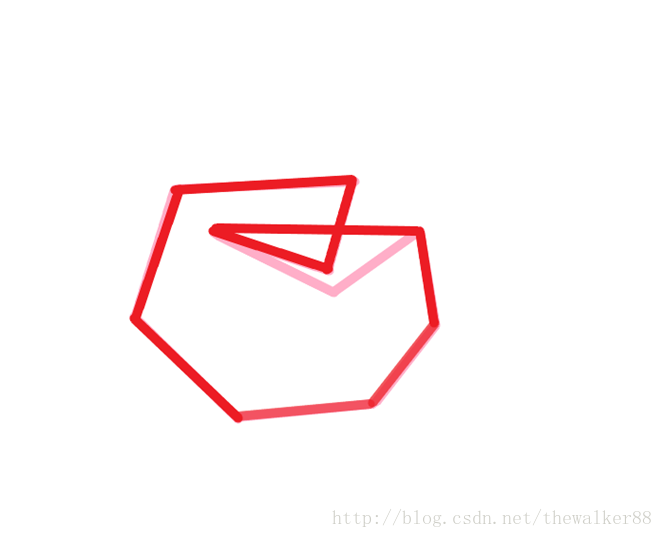

可见，Graham对于此类多边形求得的凸包将是一个复杂多边形，显然错误
因此，我们只能将其像处理点集一样，先排序再搞。
然而，这样不仅没利用上简单多边形自带的序，而且复杂度还是O（nlogn）的，很不好

因此，我现在来介绍一种由Melkman在1987年发明的，可以在O（n）的时间复杂度下求出正确的，简单多边形的凸包的Melkman算法

这个算法是基于Graham扫描线算法的，他们的大体思路相同，但是不同之处在于，Graham使用一个栈来维护凸包，而Melkman使用一个双头队列来维护凸包，每次不仅仅维护队列头的凸性，也维护队列尾的凸性，因此，它得到每时每刻都包含当前考虑过的所有的点的凸包
下面我们模拟一下
对于一个n个点的多边形，我们开一个大小为2*n的deque（即双头队列），设bot为队列尾，top为队列头，bot初始值为n-1，top初始值为n
我们把点1从前插入队列，同时top++，接下来，由于队列里只有一个点1，我们可以直接把2从队列头插入和把2从队列尾插入注意，从现在起每时每刻，队列头和队列尾的点总是同一个，也就是当前凸包里的最后考虑的点
接下来我们插入点3
我们说过，要在队列头和队列尾都维护凸性，如果队列头不是凸的，在队列头弹栈（top–），如果队列尾不是凸的，我们在队列尾弹栈（bot++），我们写程序的时候，在队列头维护一下，然后入栈，之后在队列尾维护一下，然后入栈，所以最后，我们的队列会是3 1 2 3或者3 2 1 3
这是头三个点
我们现在来考虑点4，我们看，队列头和队列正数第二个点所连成的直线，队列尾和队列倒数第二个点所连成的直线，以及剩下的凸包上的边们，会把平面分为5个部分，看图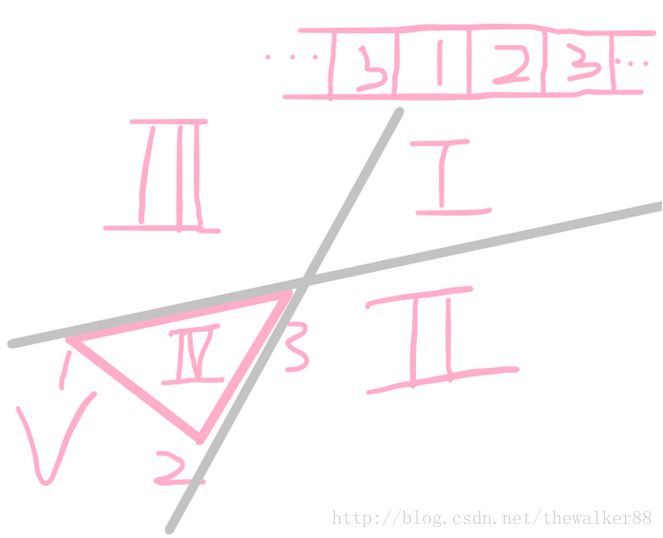
这个图
如果第四个点落在区域II，说明对列头不合法了，在队列头弹栈，如果在区域III，我们要在队列尾进行维护，如果在区域I，我们要把队列的头和尾一起进行维护，如果在区域IV说明这个点是当前所求得的凸包内部的点，明显对答案没有贡献，我们此时直接忽略这个点去看第五个点（上次用Graham跑凸包时的错误可被此情况排除）
那么，如果点落在区域V呢？？？
并不会落在区域V！
因为我们是个简单多边形，如果在区域V有点，则必然产生自交边，这是违背简单多边形的定义的。
如此进行下去，直到我们将所有的点考虑一遍，此时bot+1到top-1就是凸包上的点
时间复杂度很明显是线性的，因为每个点最多进栈出栈一次
而且此算法还是个在线算法，可以随时接收新的点，并且我最开始塞入队列中的点不必非得在凸包上，相比之下，这个算法比Graham妙得多
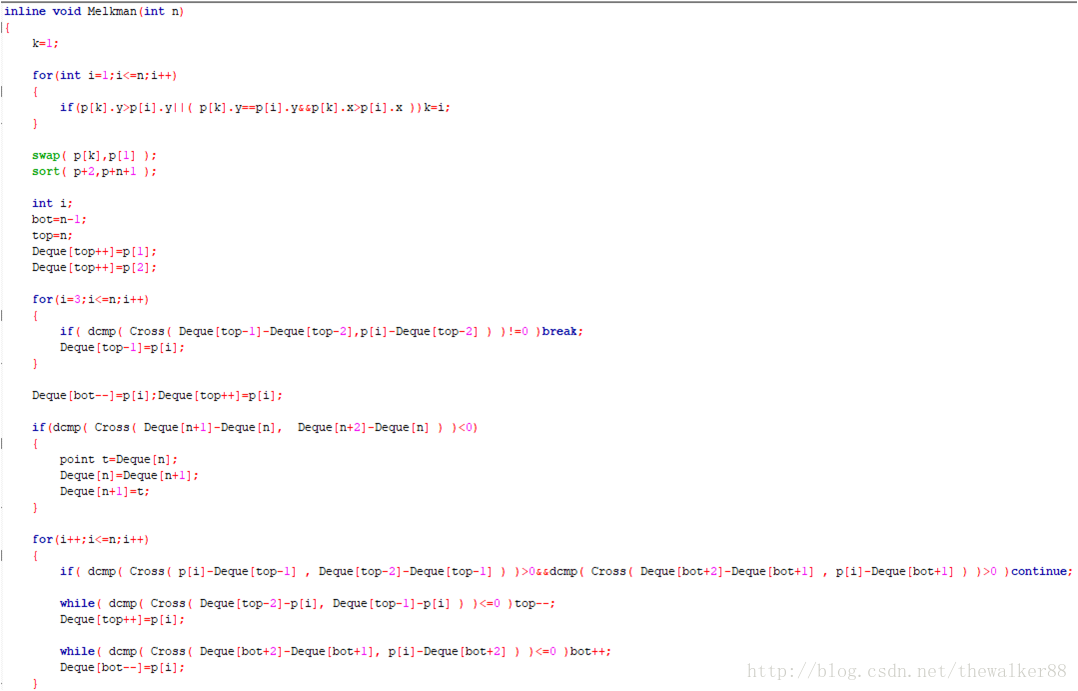
来看一下蒟蒻丑到不行的代码

实现细节：判断在什么区域时，只需要先排除IV区，接着队列头队列尾分别判断即可，无需细究究竟是什么区域
那么就是这样，通过对此博客的阅读，您：
1），明白了求简单多边形凸包时Graham错误的原因
2），学会了目前最优的凸包算法——Melkman算法
3），明白了这个博客创作者是个蒟蒻
如果您第二条收获并没有，建议您再仔细看看，因为我的博客可能是最详细的讲授Melkman算法的了
就是这样希望您有收获
我的QQ号是1145101354 ，欢迎大家加我来讨论问题（请注明来自CSDN）
以上
（还不快夸我可爱QwQ

注：本文中贴出的代码与文中的代码实现并不是完全一样
此代码是先将点1，2入队，如果1，2，3时逆时针的，则直接入3（结束后队列为：”3，1，2，3“），否则将1，2调换位置，然后入3（结束后队列为：”3，2，1，3“）
然而18.03.09晚在我正在给东北的众神犇口胡的时候，神犇Camouflager 提出，2也如同之后的点一样前后都加入队列，然后再慢慢弹栈，这样对正确性没有影响，而且代码似乎能好写点，经过思考觉得神犇就是神犇，说的话挺有道理，因此本文中对算法描述的时候采用了Camouflager的想法。这是与原论文不一样的地方。

扩展：
以上讨论的只是二维的凸包，如果延生为三维、多维的凸包问题呢？如何求解？
不过首先，二维凸包可以用来解决围栏问题、城市规划问题、聚类分析等等。但是三维、多维的凸包可能的使用范畴有哪些？

附：快包算法代码（C语言）：

#include<stdio.h>
#include<stdlib.h>

int g_result[240][2];

/*getResult()实现功能：以坐标P0(x1,y1)和Pn(x2,y2)为直线，找出pack里面里这条直线最远的点Pmax
*并找出直线P0Pmax和PmaxPn的上包，进行递归。
*注：Pack[0][0]存放点的个数，pack[1]开始存放点的坐标。
*全局变量g_result[][]用来存放凸包上的点，即最终所要的答案。同样g_result[0][0]存放的是已找到的点的个数。
**/
void getResult(int Pack[240][2], int x1, int y1, int x2, int y2)
{
    int i,t,x3,y3,R,Rmax,tmax;
    int ResultPack[240][2];
    ResultPack[0][0] = 0;
    if(Pack[0][0] <= 1)
        return; 
    x3 = Pack[1][0];
    y3 = Pack[1][1];
    R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
    Rmax = R;
    tmax = 1;
    for(i=2;i<=Pack[0][0];i++)
    {
        x3 = Pack[i][0];
        y3 = Pack[i][1];
        R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
        if(R >= 0)
        {
            t = ++ResultPack[0][0];
            ResultPack[t][0] = x3;
            ResultPack[t][1] = y3;
        }
        if(R > Rmax)
        {
            Rmax = R;
            tmax = i;
        }
    }
    if(Rmax <= 0)
    {
        for(i=1;i<ResultPack[0][0];i++)
        {
            x3 = ResultPack[i][0];
            y3 = ResultPack[i][1];
            R = x1*y2 + x3*y1 + x2*y3 - x3*y2 - x2*y1 - x1*y3;
            if(R == 0 && !((x3==x2&&y3==y2)||(x3==x1&&y3==y1)))
            {
                t = ++g_result[0][0];
                g_result[t][0] = ResultPack[i][0];
                g_result[t][1] = ResultPack[i][1];
            }
        }
        return;
    }
    else
    {
        t = ++g_result[0][0];
        g_result[t][0] = Pack[tmax][0];
        g_result[t][1] = Pack[tmax][1];
        if(ResultPack[0][0] == 0)
            return;
    }
    getResult(ResultPack,x1,y1,Pack[tmax][0],Pack[tmax][1]);
    getResult(ResultPack,Pack[tmax][0],Pack[tmax][1],x2,y2);
}

void main()
{
    int Point[240][2];//Point存所有点。
    int i=1;
    int x1,y1,x2,y2,x3,y3;
    g_result[0][0]=0;Point[0][0]=0;//Point的第一行第一列元素存放包里面有几个点。初始化为0。
    printf("请输入所有点的坐标：\n");
    while(scanf("%d,%d",&Point[i][0],&Point[i][1]) != EOF)
        i++;
    Point[0][0] = i-1;
    x1 = Point[1][0];
    y1 = Point[1][1];
    x2 = x1;
    y2 = y1;
    for(i=2;i<=Point[0][0];i++)
    {
        x3 = Point[i][0];
        y3 = Point[i][1];
        if(x3 < x1)
        {
            x1 = x3;
            y1 = y3;
        }
        else if(x3 > x2)
        {
            x2 = x3;
            y2 = y3;
        }
    }
    g_result[1][0] = x1;
    g_result[1][1] = y1;
    g_result[2][0] = x2;
    g_result[2][1] = y2;
    g_result[0][0] += 2;
    getResult(Point, x1, y1, x2, y2);
    getResult(Point, x2, y2, x1, y1);

    printf("\n\n构成凸包的点有：\n");
    for(i=1;i<=g_result[0][0];i++)
        printf("(%d,%d)\n",g_result[i][0],g_result[i][1]);
    system("pause");
}

例题（ HDU 3285 ）

Description

A lattice point is a point with integer coordinates. A lattice polygon is a polygon with all vertices lattice points.

A polygon is convex if any line segment between two points of the polygon is inside (or on the boundary of) the polygon. Equivalently, the interior angle at each polygon vertex is less than 180 degrees.

For a set S, of lattice points, the convex hull is the smallest convex (lattice) polygon which contains all points of the set. (The vertices of the convex hull must be members of the set of lattice points). If all the points are on a single straight line, the convex hull will be a line segment (a degenerate polygon – see rightmost diagram below). In the diagrams below, the points of the set are indicated by solid dots, the vertices of the convex hull by X’s and the convex hull is drawn connecting the vertices.
Note that not all points on the convex hull polygon are vertices.

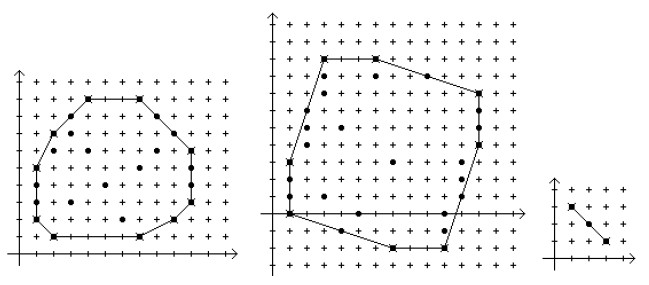
The vertices of a lattice polygon are in standard order if:
a) The first vertex is the one with the largest y value. If two vertices have the same y value, the one with the smaller x value is the first.
b) Vertices are given in clockwise order around the polygon.

Write a program that reads a set of lattice points and outputs the vertices of the convex hull of the points in standard order.

Input

The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets that follow. The first line of each data set contains the data set number, followed by a space, followed by a decimal integer giving the number of points N, (3 ≤ N ≤ 50), in the set. The remaining lines in the data set contain the points in the set, at most 5 points per line (the last line may have fewer). Each point consists of 2 space separated decimal integer values representing the x and y coordinates
respectively.

Output

For each data set there are multiple lines of output. The first line contains a decimal integer giving the data set number followed by a single space, followed by a decimal integer giving the total number of vertices of the convex hull. The vertices of the convex hull follow, one per line in standard order. Each line contains the decimal integer x coordinate, a single space and the decimal integer y coordinate.

Sample Input

4
1 25
2 1 7 1 1 2 9 2 1 3
10 3 1 4 10 4 1 5 10 5
2 6 10 6 2 7 9 7 3 8
8 8 4 9 7 9 6 2 3 3
5 4 7 5 8 6 4 6 3 7
2 30
3 9 6 9 3 8 9 8 3 7
12 7 2 6 12 6 2 5 12 5
2 4 12 4 1 3 11 3 1 2
11 2 1 1 11 1 1 0 10 0
4 -1 10 -1 7 -2 10 -2 5 0
7 3 4 5 6 8 3 1 2 6
3 3
3 1 2 2 1 3
4 6
1 3 19 1 4 2 2 1 11 2
10 1

Sample Output

1 10

4 9

7 9

10 6

10 3

9 2

7 1

2 1

1 2

1 5

2 7

2 8

3 9

6 9

12 7

12 4

10 -2

7 -2

1 0

1 3

3 2

1 3

3 1

4 4

1 3

11 2

19 1

2 1

代码：

#include <map>
#include <set>
#include <cmath>
#include <deque>
#include <queue>
#include <stack>
#include <vector>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define eps 1e-10
#define mod 1e9+7
#define PI acos(-1)
#define INF 0x3f3f3f3f
#define lowbit(x) (x&(-x))
#define read(x) scanf("%d",&x)
#define mem(a,b) memset(a,0,sizeof(a))
#define fori(a,b) for(int i=a; i<=b; i++)
#define forj(a,b) for(int j=a; j<=b; j++)
#define fork(a,b) for(int k=a; k<=b; k++)
#define ifor(a,b) for(int i=a; i>=b; i--)
#define jfor(a,b) for(int j=a; j>=b; j--)
#define kfor(a,b) for(int k=a; k>=b; k--)
#define IN freopen("in.txt","r",stdin)
#define OUT freopen("out.txt","w",stdout)

using namespace std;
typedef long long LL;

struct Point
{
    int x, y;
}p[55], stk[55];

int to_left(const Point& a, const Point& b, const Point& c)
{
    return (b.y-a.y)*(c.x-a.x) - (b.x-a.x)*(c.y-a.y);
}

int dis(const Point& a, const Point& b)
{
    return (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y);
}

bool cmp(const Point& a, const Point& b)
{
    int t = to_left(p[0], a, b);
    return t<0 || (t==0 && dis(p[0], a)<dis(p[0], b));
}

int main()
{
    int T;
    read(T);
    while(T--)
    {
        int kase, n, k = 0,top = 1;
        scanf("%d%d", &kase, &n);
        fori(0,n-1)
        {
            scanf("%d%d", &p[i].x, &p[i].y);
            if(p[i].y<p[k].y || (p[i].y==p[k].y && p[i].x<p[k].x))
                k = i;
        }
        swap(p[0], p[k]);
        sort(p+1, p+n, cmp);
        stk[0] = p[0];
        stk[1] = p[1];
        fori(2,n-1)
        {
            while(top && to_left(stk[top-1], stk[top], p[i])>=0)
                top--;
            stk[++top] = p[i];
        }
        k = 0;
        fori(1,top)
        {
            if(stk[i].y>stk[k].y || (stk[i].y==stk[k].y && stk[i].x<stk[k].x))
                k = i;
        }
        printf("%d %d\n", kase, top+1);
        ifor(k,0)
            printf("%d %d\n", stk[i].x, stk[i].y);
        ifor(top,k+1)
             printf("%d %d\n", stk[i].x, stk[i].y);
    }
    return 0;
}

参考资料：

https://blog.csdn.net/bone_ace/article/details/46239187

https://blog.csdn.net/foreverlin1204/article/details/6221986

https://blog.csdn.net/thewalker88/article/details/79504704

lxt_Lucia

关注

29
点赞
踩
104

收藏

觉得还不错? 一键收藏
2
评论
凸包 —— 五种解法

欢迎访问https://blog.csdn.net/lxt_Lucia～～宇宙第一小仙女\(^o^)/～～萌量爆表求带飞=≡Σ((( つ^o^)つ~ dalao们点个关注呗～～关于凸包，之前一直漏掉了这一个，上周末组队赛，听说有一题就是凸包的模板，可惜不会，听说不算很难，正好这周空余的课很少，就顺便搞了8... 目录前言解一：穷举法（蛮力法）解二：分治法解三...
复制链接

扫一扫