离散数学-7 二元关系

定义7.1 由两个元素 x 和 y，按照一定的顺序组成的二元组称为有序对，记作<x,y>.

有序对性质:

(1) 有序性 <x,y><y,x> （当xy时）

(2) <x,y>与<u,v>相等的充分必要条件是

<x,y>=<u,v> x=uy=v.

定义7.2 设A,B为集合，A与B的笛卡儿积记作AB，且

AB = {<x,y>| xAyB}.

笛卡儿积性质：

(1) 不适合交换律

AB BA (AB, A, B)

(2) 不适合结合律

(AB)C A(BC) (A, B, C)

(3) 对于并或交运算满足分配律

A(BC) = (AB)(AC) (BC)A = (BA)(CA)

A(BC) = (AB)(AC) (BC)A = (BA)(CA)

(4) 若 A 或 B 中有一个为空集，则 AB 就是空集.

A = B = 

(5) 若 |A| = m, |B| = n, 则 |AB| = mn

例题：

AC = BD是否推出 A=B,C=D? 为什么？

不一定.反例如下：

A={1}，B={2}, C = D = , 则AC = BD但是A B.

定义7.3 如果一个集合满足以下条件之一：

(1) 集合非空, 且它的元素都是有序对

(2) 集合是空集

则称该集合为一个二元关系, 简称为关系，记作R.

定义7.4

设A,B为集合, A×B的任何子集所定义的二元关系叫做从A到B的二元关系, 当A=B时则叫做A上的二元关系.

定义7.5 设 A 为集合,

(1) 是A上的关系，称为空关系

(2) 全域关系 E_A = {<x,y>| x∈A∧y∈A} = A×A

恒等关系 I_A = {<x,x>| x∈A}

小于等于关系 L_A = {<x,y>| x,y∈A∧x≤y}, A为实数子集

整除关系 D_B = {<x,y>| x,y∈B∧x整除y}, A为非0整数子集

包含关系 R_ = {<x,y>| x,y∈A∧xy}, A是集合族.

关系的表示

1. 关系矩阵

若A={x₁, x₂, …, x_m}，B={y₁, y₂, …, y_n}，R是从A到B的

关系，R的关系矩阵是布尔矩阵M_R = [ r_ij ] _mn, 其中

r_ij = 1 < x_i, y_j> R.

2. 关系图

若A= {x₁, x₂, …, x_m}，R是从A上的关系，R的关系图是G_R=<A, R>, 其中A为结点集，R为边集. 如果<x_i,x_j>属于关系R，在图中就有一条从 x_i 到 x_j 的有向边.

注意：

关系矩阵适合表示从A到B的关系或A上的关系（A,B为有穷集）

关系图适合表示有穷集A上的关系

关系的基本运算

定义7.6 关系的定义域、值域与域分别定义为

domR = { x | y (<x,y>R) }

ranR = { y | x (<x,y>R) }

fldR = domR  ranR

定义7.7 关系的逆运算

R^1 = { <y, x> | <x, y>R }

定义7.8 关系的合成运算

R_S = { <x, z> | y (<x, y>R  <y, z>S) }

定义7.9 设R为二元关系, A是集合

(1) R在A上的限制记作 R↾A, 其中

 R↾A = { <x,y> | xRy∧x∈A }

(2) A在R下的像记作R[A], 其中

 R[A]=ran(R↾A)

说明：

R在A上的限制 R↾A是 R 的子关系，即 R↾A R

A在R下的像 R[A] 是 ranR 的子集，即 R[A] ranR

R↾ = 

R[] = 

定理7.1 设F是任意的关系, 则

(1) (F^1)^1=F

(2) domF^1= ranF, ranF^1= domF

定理7.2 设F, G, H是任意的关系, 则

(1) (F_G)_H = F_(G_H)

(2) (F_G)^1 = G^1_F^1

定理7.3 设R为A上的关系, 则

  R_I_A= I_AR=R

定理7.4

(1) F_(GH) = F_G∪F_H (2) (G∪H)_F = G_F∪H_F

(3) F_(G∩H) F_G∩F_H (4) (G∩H)_F G_F∩H_F

只证 (3) 任取<x,y>,

 <x,y>∈F_(G∩H)

t (<x,t>∈F∧<t,y>∈G∩H)

 t (<x,t>∈F∧<t,y>∈G∧<t,y>∈H)

 t ((<x,t>∈F∧<t,y>∈G)∧(<x,t>∈F∧<t,y>∈H))

 t (<x,t>∈F∧<t,y>∈G)∧t (<x,t>∈F∧<t,y>∈H)

 <x,y>∈F_G∧<x,y>∈F_H

 <x,y>∈F_G∩F_H

所以有 F_(G∩H) F_G∩F_H

定理7.4 的结论可以推广到有限多个关系

R_(R₁∪R₂∪…∪R_n) = R_R₁∪R_R₂∪…∪R_R_n

(R₁∪R₂∪…∪R_n)_R = R_1R∪R_2R∪…∪R_nR

R_(R₁∩R₂∩ … ∩R_n) R_R₁∩R_R₂∩ … ∩R_R_n

(R₁∩R₂∩ … ∩R_n)_R R_1R∩R_2R∩ … ∩R_nR

定理7.5 设F 为关系, A, B为集合, 则

(1) F ↾(A∪B) = F ↾A∪F ↾B

(2) F [A∪B] = F [A]∪F [B]

(3) F ↾(A∩B) = F ↾A∩F ↾B

(4) F [A∩B] F [A]∩F [B]

定义7.10

设 R 为 A 上的关系, n为自然数, 则 R 的 n 次幂定义为：

(1) R⁰ = { <x,x> | x∈A } = I_A

(2) Rⁿ⁺¹ = Rⁿ_R

注意：

对于A上的任何关系 R₁ 和 R₂ 都有 R₁⁰ = R₂⁰ = I_A

对于A上的任何关系 R 都有 R¹ = R

如何计算R的n次幂呢（n≧2）？

1、关系矩阵的布尔乘法

与线性代数中的矩阵乘法公式相比，只要把矩阵乘法公式中的数乘改为合取，把数加改为析取，就得到了关系矩阵的布尔乘法公式。

2、关系图

几次幂就是走几步能不能到。

定理7.6 设 A 为 n 元集, R 是A上的关系, 则存在自然数 s 和 t, 使得 R^s = R^t.

证 R 为A上的关系,

列出 R 的各次幂

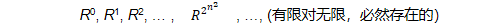
必存在自然数 s 和 t 使得 R^s = R^t

定理7.7 设 R 是 A上的关系, m, n∈N, 则 【归纳法】

(1) R^m_Rⁿ = R^m+n

(2) (R^m)ⁿ = R^mn

定理7.8 设R 是A上的关系,

若存在自然数 s, t (s<t) 使得 R^s=R^t, 则

(1) 对任何 k∈N有 R^s+k = R^t+k

(2) 对任何 k, i∈N有 R^s+kp+i = R^s+i, 其中 p = ts【归纳法】

(3) 令S = {R⁰,R¹,…,R^t1}, 则对于任意的 q∈N 有R^q∈S

定义7.11 设 R 为A上的关系,

(1) 若 x(x∈A→<x,x>R), 则称 R 在 A 上是自反的.

(2) 若 x(x∈A→<x,x>R), 则称 R 在 A 上是反自反的.

定义7.12 设 R 为 A上的关系, 

(1) 若xy( x,y∈A∧<x,y>∈R→<y,x>∈R), 则称 R 为 A上对称的关系.

(2) 若xy( x,y∈A∧<x,y>∈R∧<y,x>∈R→x=y), 则称 R 为A上的反对称关系.

定义7.13 设R为A上的关系, 若

xyz(x,y,z∈A∧<x,y>∈R∧<y,z>∈R→<x,z>∈R),则称 R 是A上的传递关系.

定理7.9 设R为A上的关系, 则

(1) R 在A上自反当且仅当 I_A R

(2) R 在A上反自反当且仅当 R∩I_A = 

(3) R 在A上对称当且仅当 R=R^1

(4) R 在A上反对称当且仅当 R∩R^1 I_A

(5) R 在A上传递当且仅当 R_R R

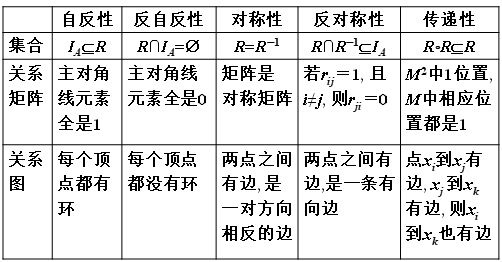
恒等关系IA和空关系既是A上的对称关系也是A上的反对称关系.

定义7.14 设R是非空集合A上的关系, R的自反(对称或传递)闭包是A上的关系R, 使得R满足以下条件：

(1) R是自反的(对称的或传递的)

(2) RR

(3) 对A上任何包含R的自反(对称或传递)关系R有RR，R的自反闭包记作r(R), 对称闭包记作s(R), 传递闭包记作t(R).

定理7.10 设R为A上的关系, 则有

(1) r(R)=R∪R⁰

(2) s(R)=R∪R^1

(3) t(R)=R∪R²∪R³∪…

说明：对有穷集A(|A|=n)上的关系, (3)中的并最多不超过Rⁿ 原因是R的n次幂相当于走了n步，可以联系关系图来思考，在R的关系图中, 从顶点xi到xj且不含回路的路径最多n步长.。

我们希望R有某些有用的性质，并且添加的有序对要尽可能少，这样就构造了闭包。

推论：设R为有穷集A上的关系，则存在正整数r使得： t(R)=R∪R²∪R³∪…R^r

以定理为基础，我们可以得到构造闭包的方法：

（1）根据定理7.10通过集合运算求得。

（2）利用关系矩阵求闭包。

设关系R、r(R)、s(R)、t(R)的关系矩阵分别是M、M_r、M_s和M_t，定理7.10中的公式转换成矩阵表示：

M_r = M + E

M_s = M + M^T

M_t = M + M² + M³ +…

其中， E：与M同阶的单位矩阵。

M^T：M的转置。

"+"：矩阵中对应元素的逻辑加(按位或)。

（3）利用关系图求闭包。

设关系R、r(R)、s(R)、t(R)的关系图分别是G、Gr、Gs和Gt ，则Gr、Gs、Gt的顶点集与G的顶点集相等。除了G的边以外，依下述方法添加新的边：

Gr：考察G的每个顶点，如果没有环就加上一个环，最终得到的是Gr。

Gs：考察G的每一条边，如果有一条x_i到x_j的单向边，i≠j，则在G中加一条x_j到x_i的反方向边．最终得到Gs。

Gt：考察G 的每个顶点 x_i, 找 x_i可达的所有顶点 x_j(允许i=j )，如果没有从 x_i 到 x_j的边, 就加上这条边, 得到图Gt。

定理7.11 设R是非空集合A上的关系, 则

(1) R是自反的当且仅当 r(R)=R.

(2) R是对称的当且仅当 s(R)=R.

(3) R是传递的当且仅当 t(R)=R.

定理7.12 设R₁和R₂是非空集合A上的关系, 且 R₁R₂, 则

(1) r(R₁) r(R₂)

(2) s(R₁) s(R₂)

(3) t(R₁) t(R₂)

定理7.13 设R是非空集合A上的关系,

(1) 若R是自反的, 则 s(R) 与 t(R) 也是自反的

(2) 若R是对称的, 则 r(R) 与 t(R) 也是对称的

(3) 若R是传递的, 则 r(R) 是传递的.

说明：如果需要进行多个闭包运算，比如求R的自反、对称、传递的闭包 tsr(R)，运算顺序如下：tsr(R) = rts(R) = trs®

定理7.13

（1）如果关系R是自反的，那么经过求闭包的运算以后所得到的关系仍旧是自反的。

（2）如果关系R是对称的，那么经过求闭包的运算以后所得到的关系仍旧是对称的。

（3）但是对于传递的关系则不然，它的自反闭包仍旧保持传递性，而对称闭包就有可能失去传递性。

因此，在计算关系R的自反、对称、传递的闭包时, 为了不失传递性, 传递闭包运算应放在对称闭包运算的后边.

定义7.15 设R为非空集合上的关系. 如果R是自反的、对称的和传递的, 则称R为A上的等价关系. 设 R 是一个等价关系, 若<x,y>∈R, 称 x等价于y, 记做x～y.

定义7.16 设R为非空集合A上的等价关系, x∈A，令

 [x]_R = {y | y∈A∧xRy}

定理7.14 设R是非空集合A上的等价关系, 则

(1) xA, [x]是A的非空子集

(2) x,yA, 如果 xRy, 则 [x] = [y]

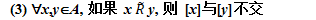
(4) ∪{[x] | xA}=A

证 (1) 由定义, xA有[x]A. 又x[x], 即[x]非空.

(2) 任取 z, 则有

 z∈[x]  <x,z>∈R <z,x>∈R

<z,x>R∧<x,y>R <z,y>R <y,z>R

从而证明了z∈[y]. 综上所述必有 [x][y]. 同理可证 [y][x]. 这就得到了[x] = [y].

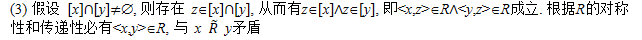
(4) 先证∪{[x] | xA} A. 任取y,

y∪{[x] | xA} x(xA∧y[x])

y[x]∧[x] A yA

从而有∪{[x] | x∈A} A

再证A ∪{[x] | x∈A}. 任取y,

yA y[y]∧yA y∈∪{[x] | xA}

从而有∪{[x] | x∈A} A成立.

综上所述得∪{[x] | xA} = A.

定义7.17 设 R 为非空集合A上的等价关系, 以 R 的所有等价类作为元素的集合称为A关于R的商集, 记做A/R, A/R = {[x]R | x∈A}

实例 设 A={1,2,…,8}，A关于模3等价关系R的商集为

A/R = {{1,4,7}, {2,5,8}, {3,6}}

定义7.18 设A为非空集合, 若A的子集族π(π P(A))满足:

(1) π

(2) xy(x,yπ∧x≠y→x∩y=)【两两不交】

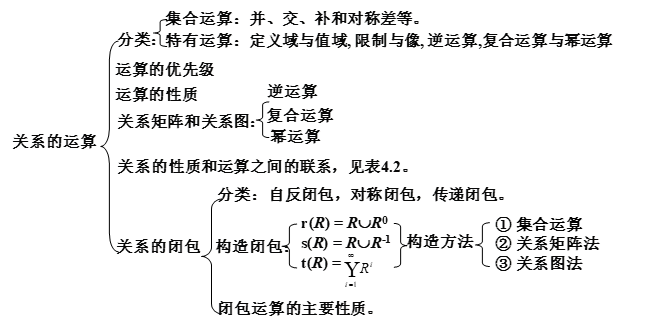
(3) ∪π = A

则称π是A的一个划分, 称π中的元素为A的划分块.

根据等价类的性质以及划分的定义，显然有下面的结论：

（1）商集就是A的一个划分，等价类就是划分块。

（2）给定集合A上的一个等价关系R决定了A的一个划分，并且不同的等价关系将对应于不同的划分。

（3）给定集合A的一个划分确定该集合上的一个等价关系。

定义4.17 设R为非空集合A上的关系，如果R是自反的和对称的，则称R为A上的相容关系。

根据该定义，相容关系有以下三个性质：

（1）所有的等价关系都是相容关系。

（2）相容关系的关系矩阵主对角线全为1且是对称矩阵。

（3）相容关系的关系图每一个节点上都有环，且每两个不同节点间如果有边，一定有方向相反的两条边。

相容关系的图形表示中，每个环不必画出，两个元素之间方向相反的有向边用一条无向边替代，这样的图称为相容关系的简化关系图。

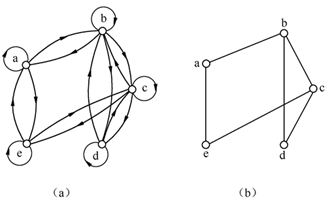
定义4.18 设R是非空集合A上的相容关系，集合C A，若对任意的x, yC都有xRy成立，则称C是由相容关系R产生的相容类。

如果R是A上的相容关系, C是由相容关系R产生的相容类,从定义可看出:

（1）相容类C一定是A的子集。

（2）因为相容关系R是自反的，即xA， 有xRx，所以{x}是由相容关系R产生的一个相容类，即A中的任何元素组成的单元素集是由相容关系R产生的一个相容类。

定义4.19 设R是非空集合A上的相容关系，C是R产生的相容类。如果它不是其他任何相容类的真子集，则称C为最大相容类，记为C_R。

根据定义4.19，最大相容类C_R具有如下的性质：

（1）C_R中任意元素x与C_R中的所有元素都有相容关系R。

（2）A - C_R中没有一个元素与C_R中的所有元素都有相容关系R。

利用相容关系的简化关系图求最大相容类的方法：

（1）最大完全多边形的顶点构成的集合是最大相容类。

（2）孤立点构成的集合是最大相容类。

（3）如果一条边不是任何完全多边形的边，则它的两个端点构成的集合是最大相容类。

   

定理4.20 设R是非空有限集合A上的相容关系，C是R产生的相容类，那么必存在最大相容类C_R，使得CC_R。

定义4.20 设A是非空集合，若A的子集族满足以下条件：

（1）

（2）

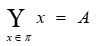
则称为集合A的一个覆盖。

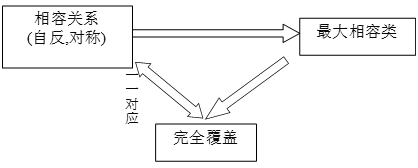
定理4.21 设A是有限集合，R是A上的相容关系，由R产生的所有最大相容类构成的集合是A的覆盖，叫作集合A的完全覆盖，记为C_R(A)。

定理4.22 给定集合A的覆盖{A₁, A₂,... ,A_n}，则由它确定的关系R= A₁A₁A₂A₂... A_nA_n是A上的相容关系。

定理4.23 集合A上的相容关系R与完全覆盖C_R(A)存在一一对应。

   

定义7.19

偏序关系：非空集合A上的自反、反对称和传递的关系，记作≼. 设≼为偏序关系, 如果 <x, y> ∈≼, 则记作 x ≼ y, 读作x"小于或等于"y.

定义7.20 设 R 为非空集合A上的偏序关系,

(1) x, y∈A, x与y可比  x ≼ y∨y ≼ x

(2) 任取元素 x 和 y, 可能有下述几种情况发生：x ≺ y (或 y ≺ x), x＝y, x与y不是可比的

定义7.21 R 为非空集合A上的偏序关系, x,y∈A, x与y都是可比的，则称R为全序（或线序）

定义7.22 x,y∈A, 如果 x≺y 且不存在 z∈A 使得 x≺z≺y, 则称 y覆盖x.

定义7.23 集合A和A上的偏序关系≼一起叫做偏序集, 记作<A,≼>.

哈斯图: 利用偏序关系的自反、反对称、传递性进行简化的关系图

特点：

(1) 每个结点没有环

(2) 两个连通的结点之间的序关系通过结点位置的高低表示，位置低的元素的顺序在前

(3) 具有覆盖关系的两个结点之间连边

偏序集<A, ≤>的哈斯图的画法如下：

（1）用"°"表示A中的每一个元素；

（2）x, yA，若x<y，则把x画在y的下面；

（3）x, yA，若y盖住x ，则用一条线段连接x和y。

定义7.24 设<A,≼>为偏序集, BA, y∈B

(1) 若x(x∈B→y≼x)成立, 则称 y 为B的最小元

(2) 若x(x∈B→x≼y)成立, 则称 y 为B的最大元

(3) 若x(x∈B∧x≼y→x=y)成立, 则称 y 为B的极小元

(4) 若x(x∈B∧y≼x→x=y)成立, 则称 y 为B的极大元

性质：

(1) 对于有穷集，极小元和极大元一定存在，可能存在多个.

(2) 最小元和最大元不一定存在，如果存在一定惟一.

(3) 最小元一定是极小元；最大元一定是极大元.

(4) 孤立结点既是极小元，也是极大元.

定义7.25 设<A, ≼>为偏序集, BA, y∈A

(1) 若x(x∈B→x≼y)成立, 则称y为B的上界

(2) 若x(x∈B→y≼x)成立, 则称y为B的下界

(3) 令C＝{y| y为B的上界}, C的最小元为B的最小上界或上确界

(4) 令D＝{y| y为B的下界}, D的最大元为B的最大下界或下确界

   

性质：

(1) 下界、上界、下确界、上确界不一定存在

(2) 下界、上界存在不一定惟一

(3) 下确界、上确界如果存在，则惟一

(4) 集合的最小元是其下确界，最大元是其上确界；反之不对.

   

   

   

关系性质的证明方法

1. 证明R在A上自反

任取x,

xA  ……………………..….…….  <x,x>R

前提 推理过程 结论

2. 证明R在A上对称

任取<x,y>，

<x,y> R  ……………………………….  <y,x>R

前提 推理过程 结论

3. 证明R在A上反对称

任取<x,y>，

<x,y>R<y,x>R  ……………………..  x = y

前提 推理过程 结论

4. 证明R在A上传递

任取<x,y>,<y,z>，

<x,y>R<y,z>R  ……………………..  <x,z>R

前提 推理过程 结论

关系等式或包含式的证明方法

数学归纳法（主要用于幂运算）

证明中用到关系运算的定义和公式, 如：

• xdomR  y(<x,y>R)
• yranR  x(<x,y>R)
• <x,y>R  <y,x>R^1
• <x,y>R∘S  t (<x,t>RÙ<t,y>S)
• <x,y>R ↾A  xA  <x,y>R
• yR A]  x (xA  <x,y>R)
• r(R) = RI_A
• s(R) = RR^1
• t(R) = RR…

   

基本要求

熟练掌握关系的三种表示法

能够判定关系的性质（等价关系或偏序关系）

掌握含有关系运算的集合等式

掌握等价关系、等价类、商集、划分、哈斯图、偏序集等概念

计算A´B, dom R, ranR, fldR, R-1, R°S , Rn , r(R), s(R), t(R)

求等价类和商集A/R

给定A的划分p，求出p 所对应的等价关系

求偏序集中的极大元、极小元、最大元、最小元、上界、下界、上确界、下确界

掌握基本的证明方法

证明涉及关系运算的集合等式

证明关系的性质、证明关系是等价关系或偏序关系7和