离散数学-2 命题逻辑等值演算

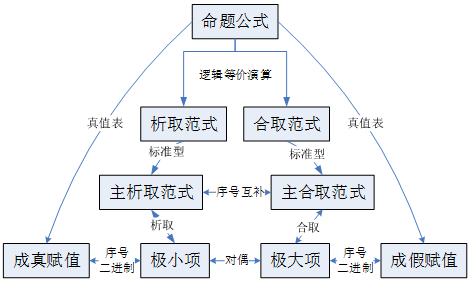
求公式主析取范式的方法步骤:

方法一：等值演算

设公式A含命题变项p₁,p₂,…,p_n

(1) 求A的析取范式A=B₁B₂ … B_s , 其中B_j是简单合取

式 j=1,2, … ,s

(2) 若某个B_j既不含p_i, 又不含Øp_i, 则将B_j展开成

B_j B_j(p_ip_i)  (B_jp_i)(B_jp_i)

重复这个过程, 直到所有简单合取式都是长度为n的极

小项为止

(3) 消去重复出现的极小项, 即用m_i代替m_im_i

(4) 将极小项按下标从小到大排列

方法二：真值表

(1) 写出A的真值表

(2)求出A的成真赋值

(3) 写出成真赋值对应的极小项，按角标从小到大析取

  

求公式的主合取范式的步骤:

方法一：等值演算

设公式A含命题变项p₁,p₂,…,p_n

(1) 求A的合取范式A=B₁B₂ … B_s , 其中B_j是简单析取

式 j=1,2, … ,s

(2) 若某个B_j既不含p_i, 又不含Øp_i, 则将B_j展开成

B_j B_j(p_ip_i)  (B_jp_i)(B_jp_i)

重复这个过程, 直到所有简单析取式都是长度为n的极

大项为止

(3) 消去重复出现的极大项, 即用M_i代替M_iM_i

(4) 将极大项按下标从小到大排列

方法二：真值表

(1) 写出A的真值表

(2)求出A的成假赋值

(3) 写出成假赋值对应的极大项，按角标从小到大合取

方法三：由主析取范式求主合取范式

  

主范式的应用

1.求公式的成真成假赋值

设公式A含n个命题变项, A的主析取范式有s个极小项, 则A

有s个成真赋值, 它们是极小项下标的二进制表示, 其余2ⁿ-s

个赋值都是成假赋值

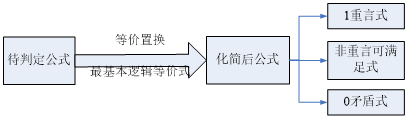
2. 判断公式的类型

设A含n个命题变项.

A为重言式 A的主析取范式含全部2ⁿ个极小项

A的主合取范式不含任何极大项, 记为1.

A为矛盾式 A的主合析取范式含全部2ⁿ个极大项

A的主析取范式不含任何极小项, 记为0.

A为非重言式的可满足式

A的主析取范式中至少含一个、但不是全

部极小项

A的主合取范式中至少含一个、但不是全

部极大项.

3. 判断两个公式是否等值

4. 解实际问题

  

  

  

  

  

  

  

  

定义2.1 若等价式AB是重言式，则称A与B等值，记作AB，并称AB是等值式

16组等值式模式

双重否定律 AA

幂等律 AAA, AAA

交换律 ABBA, ABBA

结合律 (AB)CA(BC), (AB)CA(BC)<