定义:
一个隐马尔可夫模型 (HMM) 是一个五元组:
(ΩX , ΩO, A, B, π )
其中:
ΩX = {q1,...qN}:状态的有限集合
ΩO = {v1,...,vM}:观察值的有限集合
A = {aij},aij = p(Xt+1 = qj |Xt = qi):转移概率
B = {bik},bik = p(Ot = vk | Xt = qi):输出概率
π = {πi}, πi = p(X1 = qi):初始状态分布
问题:
令 λ = {A,B,π} 为给定HMM的参数,
令 σ = O1,...,OT 为观察值序列,
隐马尔可夫模型(HMM)的三个基本问题:
评估问题:对于给定模型,求某个观察值序列的概率p(σ|λ) ;
解码问题:对于给定模型和观察值序列,求可能性最大的状态序列;
学习问题:对于给定的一个观察值序列,调整参数λ,使得观察值出现的概率p(σ|λ)最大。
算法:
评估问题:向前算法
解码问题:韦特比(Viterbi)算法
学习问题:向前向后算法,是EM算法的一个特例,带隐变量的最大似然估计
向前算法:
定义前向变量为HMM在时间t输出序列O1…Ot,并且位于状态Si的概率:
迭代公式为:
结果为:
韦特比(Viterbi)算法:
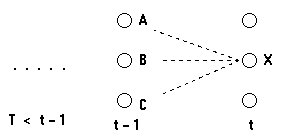
我们可以计算所有到状态 X 的路径的概率,找到其中最可能的路径,也就是局部最优路径。注意到这里,到达X的路径必然会经过 t-1 时刻的 A、B 和 C,所以我们可以利用之前的结果。达到X的最可能的路径就是下面三个之一:
(状态序列),. . .,A,X (状态序列),. . .,B,X (状态序列),. . .,C,X
我们需要做的就是找到以 AX、BX 和 CX 结尾的路径中概率最大的那个。
根据一阶马尔科夫的假设,一个状态的发生之和之前的一个状态有关系,所以X在某个序列的最后发生的概率只依赖于其之前的一个状态:
将上面这个表达式推广一下,就可以得到 t 时刻可观察状态为 kt 的状态路径最大概率的计算公式(i代表最后一个状态):
其中 aji 表示从状态 j 转移到状态 i 的概率,bikt 表示状态i时观察成 kt 的概率。












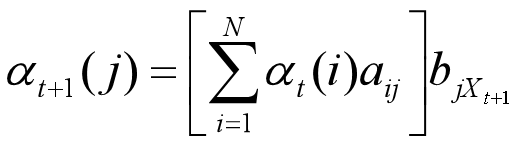
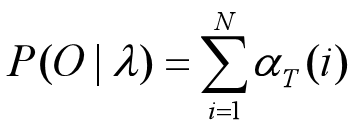
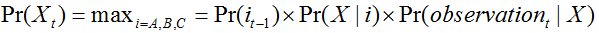
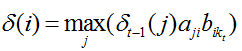














 4507
4507

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








