不废话。
证法一
如下图,三角形ABC与它的外接圆:
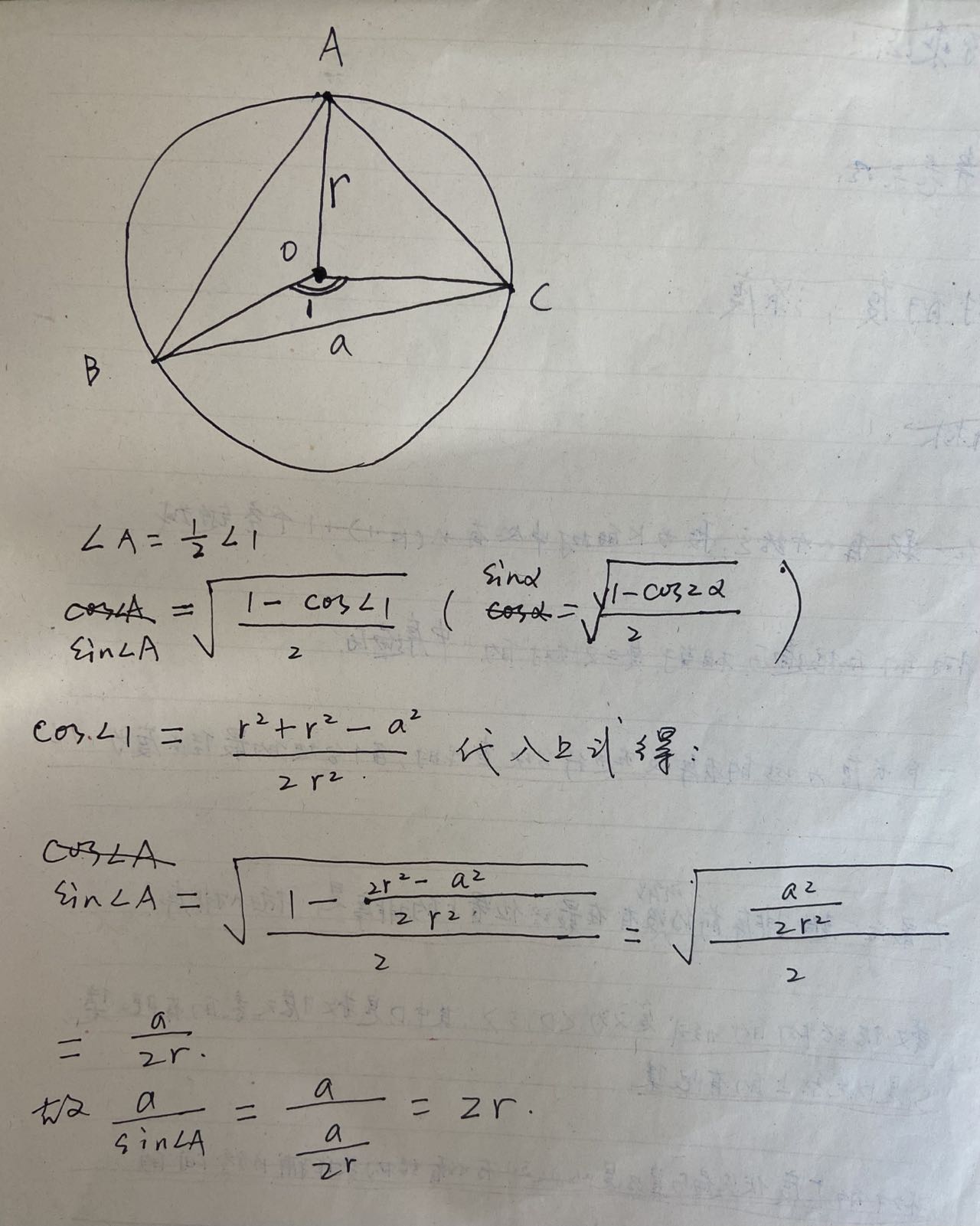
该结论的证明需要用到余弦公式。
该证明还用到了2倍角公式。即:
c o s 2 x = c o s 2 x − s i n 2 x = 1 − 2 s i n 2 x = 2 c o s 2 x − 1 cos 2 x = cos^2x - sin ^ 2x = 1-2sin^2x = 2cos^2x - 1 cos2x=cos2x−sin2x=1−2sin2x=2cos2x−1
c o s 2 x = c o s 2 x + 1 2 cos ^2 x = \frac{ cos2x + 1}{2} cos2x=2cos2x+1
s i n 2 x = 1 − c o s 2 x 2 sin ^ 2 x = \frac{ 1 - cos2x }{2} sin2x=21−cos2x
另外,该定理的证明还用到了"圆心角等于圆周角的两倍"这一个结论。
证法二
如下图推导:
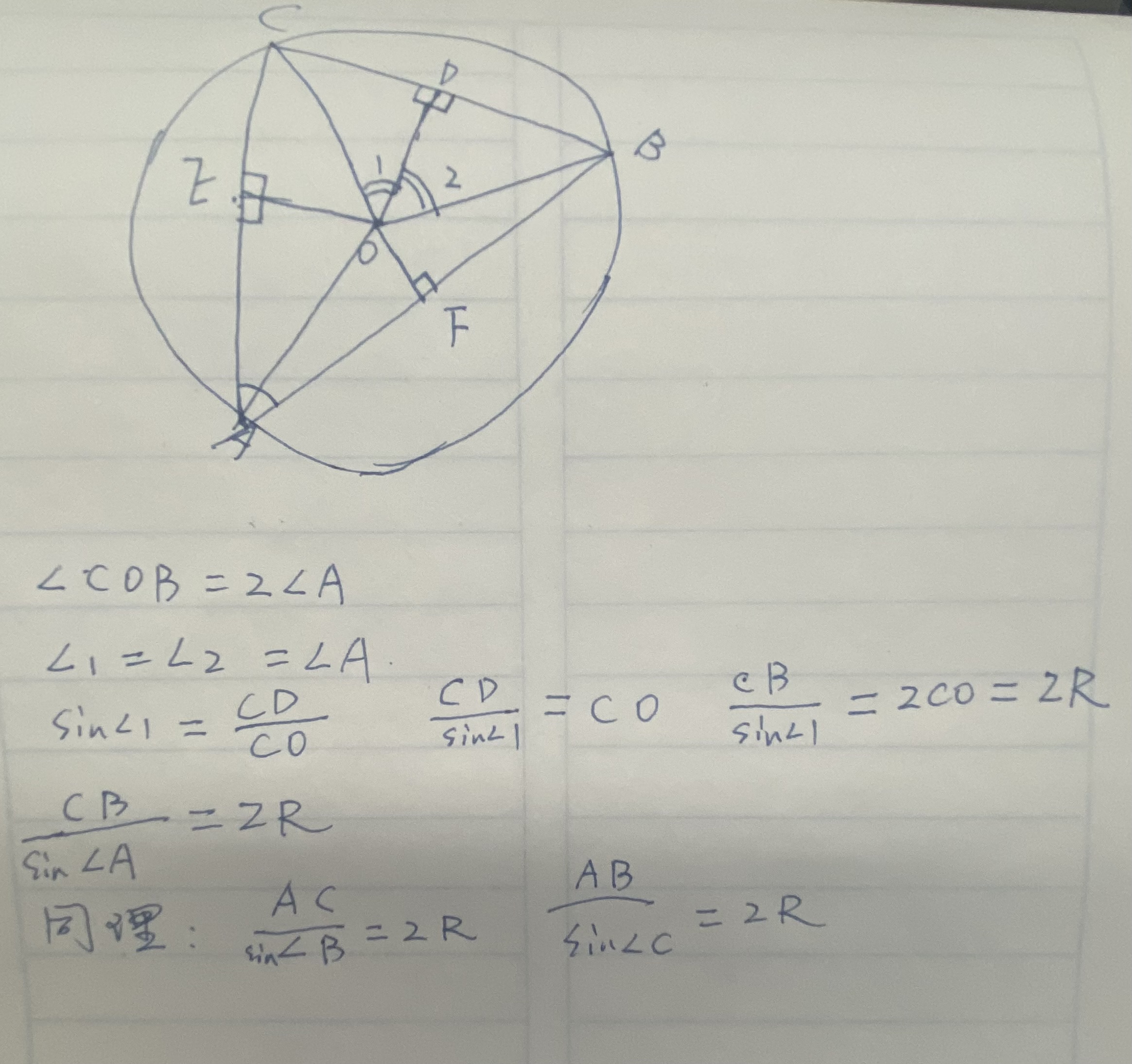

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








