- 三角形的外心
即三角形的外接圆的中心。此时:
A O = B O = C O AO = BO = CO AO=BO=CO
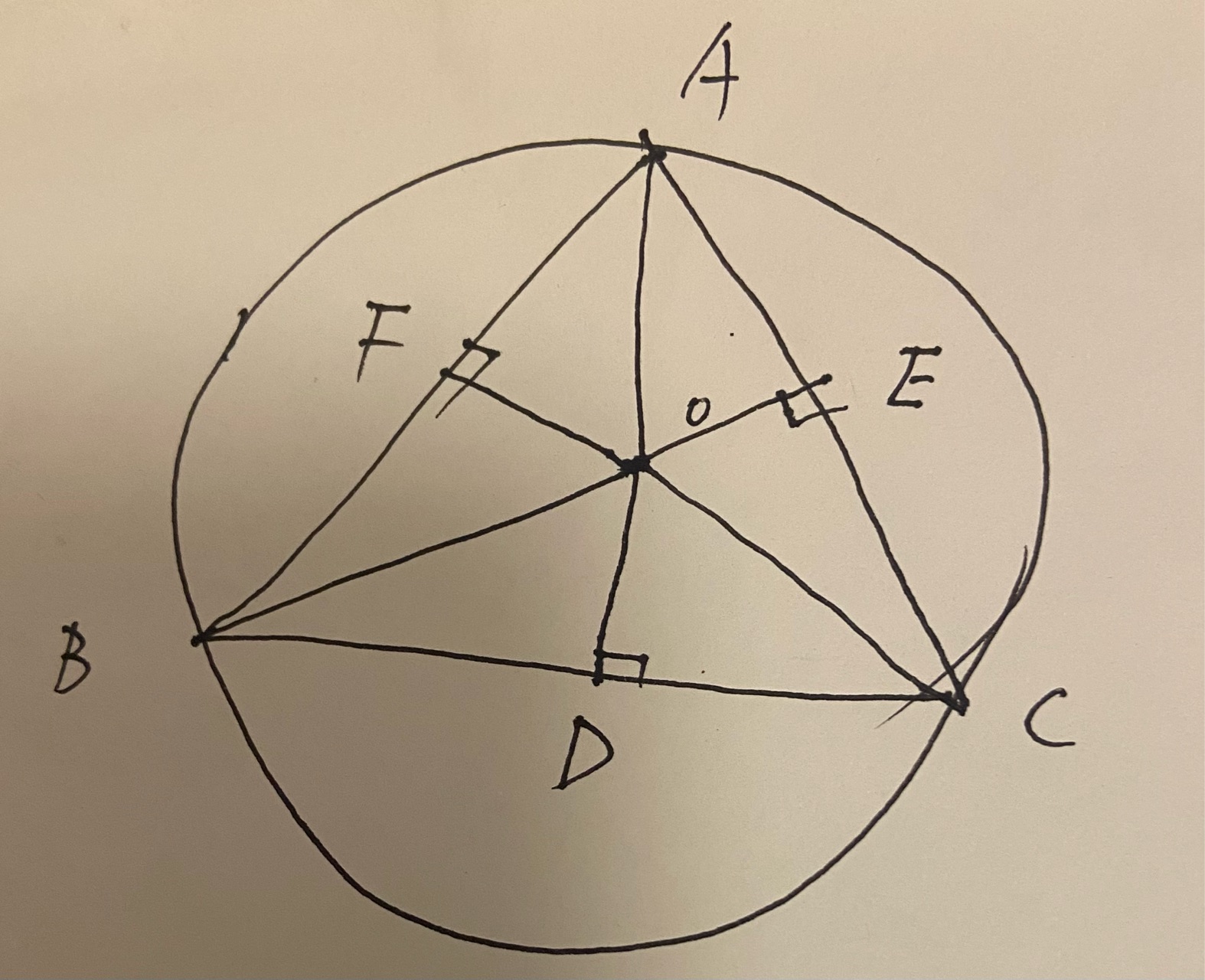
需要注意的有以下几点:
第一, A O D , B O E , C O F 不一定是直线,能否证明? \color{red}AOD,BOE,COF不一定是直线,能否证明? AOD,BOE,COF不一定是直线,能否证明?
第二, ∠ B A C 等于 ∠ B O D , sin ∠ A = a 2 / R = a 2 R \angle BAC等于\angle BOD, \sin \angle A = \frac{a}{2} /R=\frac{a}{2R} ∠BAC等于∠BOD,sin∠A=2a/R=2Ra
第三, S △ A B C = 1 2 a b sin ∠ C = 1 2 a b c 2 R = a b c 4 R S \triangle ABC = \frac{1}{2} ab \sin\angle C = \frac{1}{2}ab\frac{c}{2R} =\frac{abc}{4R} S△ABC=21absin∠C=21ab2Rc=4Rabc
- 三角形的内心
即内接圆的圆心。
需要注意的有以下几点:
第一, B O E , C O D , A O F 不一定是直线。 \color{red}BOE,COD, AOF 不一定是直线。 BOE,COD,AOF不一定是直线。
第二, ∠ B O C = 90 ° + ∠ A \angle BOC = 90\degree +\angle A ∠BOC=90°+∠A
证明: ∠ B O C = 180 ° − 180 ° − ∠ A 2 = 90 ° − ∠ A 2 \angle BOC = 180 \degree - \frac{180 \degree - \angle A}{2} =90\degree -\frac{\angle A}{2} ∠BOC=180°−2180°−∠A=90°−2∠A
第三, S △ A B C = 1 2 ( a + b + c ) r ( r 为内接圆半径 ) S_{\triangle ABC} =\frac{1}{2}(a+b+c)r(r为内接圆半径) S△ABC=21(a+b+c)r(r为内接圆半径)
第四, B D = B F = 1 2 ( a + c − b ) BD = BF = \frac{1}{2}(a + c - b) BD=BF=21(a+c−b)

- 三角形的重心
三角形三条中线的交点。
性质:
第一, A O O E = 2 1 \frac{AO}{OE} = \frac{2}{1} OEAO=12
证明:延长AOE至G点并使得EG=OE,根据定理“对角线平分的四边形为平行四边形”可以证明OBGC为平行四边形,可得AO=OG,因此可以证明AO=2OE。
第二, S △ A O B = S △ C O B = S △ C O A S_{\triangle AOB} =S_{\triangle COB} =S_{\triangle COA} S△AOB=S△COB=S△COA
证明:
第三,三个向量之和OA+OB+OC= 0
第四, A , B , , C 的坐标为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , 重心 O 点的坐标 x = x 1 + x 2 + x 3 2 , y = y 1 + y 2 + y 3 2 A,B,,C的坐标为(x_1,y_1),(x_2,y_2),(x_3,y_3),重心O点的坐标x=\frac{x_1 + x_2 + x_3}{2},y=\frac{y_1+y_2+y_3}{2} A,B,,C的坐标为(x1,y1),(x2,y2),(x3,y3),重心O点的坐标x=2x1+x2+x3,y=2y1+y2+y3

- 三角形的垂心
三角形三边上的高的交点。
- 三角形的中心
等边三角形的外心、内心、重心、垂心交于一点,该点称为三角形的中心。
- 三角形的费马点


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








