月之暗面新发布： MUON 在 LLM 训练中的可扩展性

X.Cristiano

已于 2025-02-23 21:31:23 修改

阅读量1.3k

点赞数 26

文章标签： MUON KIMI MoE 深度学习

于 2025-02-23 13:17:20 首次发布

本文链接：https://blog.csdn.net/m0_37733448/article/details/145808464

版权

MUON 在 LLM 训练中的可扩展性

摘要

最近，基于矩阵正交化的 Muon 优化器（K. Jordan 等人，2024 年）在训练小型语言模型方面表现出色，但其在更大规模模型上的可扩展性尚未得到验证。我们确定了 Muon 放大的两个关键技术：（1）添加权重衰减；（2）仔细调整每个参数的更新规模。这些技术使 Muon 能够在大规模训练中直接使用，无需超参数调整。根据扩展定律实验，Muon 的计算效率比 AdamW 高约 2 倍，在计算最优训练中表现出色。基于这些改进，我们引入了 Moonlight，这是一个使用 Muon 训练的 3B/16B 参数专家混合（MoE）模型，使用了 5.7T 个标记。我们的模型改进了当前的帕累托前沿，在训练 FLOPs 明显减少的情况下实现了更好的性能。我们开源了我们的分布式 Muon 实现，该实现具有内存最优性和通信效率。我们还发布了预训练、指令调整和中间检查点，以支持未来的研究。
在这里插入图片描述

1 引言

大型语言模型（LLMs）的快速发展显著推动了通用人工智能的进步。然而，训练强大的 LLMs 仍然是一个计算密集型和资源需求巨大的过程，这归因于扩展定律。优化器在高效有效地训练 LLMs 中起着至关重要的作用，Adam 及其变体 AdamW 是大多数大规模训练的标准选择。

最近的优化算法发展显示出超越 AdamW 的潜力。其中，K. Jordan 等人在 2024 年提出的 Muon 通过使用 Newton-Schulz 迭代对矩阵参数进行正交化梯度动量更新。Muon 的初始实验在小规模语言模型训练中表现出色。然而，正如该博客（K. Jordan 等人，2024 年）所讨论的，几个关键挑战仍未解决：（1）如何将基于矩阵正交化的优化器有效扩展到具有数十亿参数的大型模型，这些模型使用数万亿个标记进行训练；（2）如何在分布式环境中计算近似正交化；（3）这种优化器是否可以在包括预训练和监督微调（SFT）在内的不同训练阶段进行泛化。

在本技术报告中，我们提出了一项综合研究，解决了这些挑战。我们的工作基于 Muon，同时系统地识别并解决了其在大规模训练场景中的局限性。我们的技术贡献包括：

Muon 有效扩展的分析：通过广泛的分析，我们确定权重衰减在 Muon 的可扩展性中起着至关重要的作用。此外，我们提出了对 Muon 的参数级更新规则进行调整。这些调整使 Muon 能够直接使用，无需超参数调整，并显著提高了训练稳定性。
高效的分布式实现：我们开发了 Muon 的分布式版本，采用 ZeRO-1 风格的优化，实现了内存效率和通信开销的减少，同时保持了算法的数学属性。
扩展定律验证：我们进行了扩展定律研究，比较了 Muon 和强大的 AdamW 基线，并展示了 Muon 的卓越性能（见图 1a）。根据扩展定律结果，Muon 在计算最优设置下仅需要 AdamW 训练对应模型的大约 52% 的训练 FLOPs 即可实现相当的性能。

我们的综合实验表明，Muon 可以有效地取代 AdamW，成为大规模 LLM 训练的标准优化器，在训练效率和模型性能方面提供了显著的改进。因此，我们发布了使用 Muon 训练的 16B 参数 MoE 模型 Moonlight，以及我们的实现和中间训练检查点，以促进未来在 LLMs 可扩展优化技术方面的研究。

2 方法

2.1 背景

Muon 优化器：Muon（K. Jordan 等人，2024 年）最近被提出用于优化可表示为矩阵的神经网络权重。在迭代 t 时，给定当前权重 Wt−1、动量 µ、学习率 ηt 和目标 Lt，Muon 优化器的更新规则如下：

Mt = µMt−1 + ∇Lt(Wt−1)
Ot = Newton-Schulz(Mt)
Wt = Wt−1 − ηtOt

这里，Mt 是迭代 t 时的梯度动量，在 t = 0 时设置为零矩阵。在方程 1 中，采用 Newton-Schulz 迭代过程来近似求解 (MtMT t )−1/2Mt。令 UΣVT = Mt 为 Mt 的奇异值分解（SVD），则有 (MtMT t )−1/2Mt = UVT，这正交化了 Mt。直观上，正交化可以确保更新矩阵是同构的，防止权重沿几个主要方向学习。

Newton-Schulz 迭代用于矩阵正交化：方程 1 通过迭代过程计算。首先，设置 X0 = Mt/∥Mt∥F。然后，在每次迭代 k 中，根据以下公式更新 Xk 从 Xk−1：

Xk = aXk−1 + b(Xk−1XT k−1)Xk−1 + c(Xk−1XT k−1)2Xk−1

其中 XN 是经过 N 步迭代过程后的结果。这里 a、b、c 是系数。为了确保方程 2 的正确收敛，需要调整系数，使多项式 f(x) = ax + bx3 + cx5 在接近 1 的地方有一个固定点。在 K. Jordan 等人（2024 年）的原始设计中，系数设置为 a = 3.4445，b = −4.7750，c = 2.0315，以使迭代过程对较小的初始奇异值更快收敛。在本工作中，我们遵循相同的系数设置。

在范数约束下的最陡下降：Bernstein 等人（2024 年）提出将深度学习中的优化过程视为在范数约束下的最陡下降。从这个角度来看，我们可以将 Muon 和 Adam（Kingma 等人，2015 年；Loshchilov 等人，2019 年）之间的差异视为范数约束的差异。虽然 Adam 是在动态调整的 Max-of-Max 范数下的最陡下降，但 Muon 提供了一个在某些较大的 p 的 Schatten-p 范数范围内的静态范数约束。当方程 1 准确计算时，Muon 提供的范数约束将是谱范数。神经网络的权重作为输入空间或隐藏空间上的算子，通常是（局部）欧几里得空间，因此权重上的范数约束应该是诱导算子范数（或权重矩阵的谱范数）。从这个意义上说，Muon 提供的范数约束比 Adam 提供的更合理。

2.2 扩展 Muon

权重衰减：虽然 Muon 在小规模上显著优于 AdamW，如 K. Jordan 等人（2024 年）所示，但我们发现当扩展到使用更多标记训练的较大模型时，性能提升会减弱。我们观察到权重和层输出的 RMS 都在不断增长，超过了 bf16 的高精度范围，这可能会损害模型的性能。为了解决这个问题，我们引入了标准的 AdamW（Loshchilov 等人，2019 年）权重衰减机制到 Muon 中：

Wt = Wt−1 − ηt(Ot + λWt−1)

我们对有和没有权重衰减的 Muon 进行了实验，以了解其对 LLMs 训练动态的影响。根据我们在第 3.2 节中的扩展定律研究，我们训练了一个 800M 参数模型，使用了 100B 个标记（约为最优训练标记的 5 倍）。图 2 显示了使用 AdamW、原始 Muon（无权重衰减）和带权重衰减的 Muon 训练的模型的验证损失曲线。虽然原始 Muon 初始收敛速度更快，但我们观察到一些模型权重随着时间的推移变得过大，可能限制了模型的长期性能。添加权重衰减解决了这个问题——结果表明，带权重衰减的 Muon 在过训练阶段优于原始 Muon 和 AdamW，实现了更低的验证损失。因此，我们调整更新规则为方程 3，其中 λ 是权重衰减比率。

一致的更新 RMS：Adam 和 AdamW 的一个重要属性是它们保持理论更新 RMS 约为 1。然而，我们发现 Muon 的更新 RMS 取决于参数的形状，根据以下引理：

引理 1：对于形状为 [A, B] 的满秩矩阵参数，其理论 Muon 更新 RMS 为 √(1 / max(A, B))。

证明见附录 A。我们在训练过程中监控了 Muon 的更新 RMS，发现它通常接近上述理论值。我们注意到这种不一致性在扩展模型大小时可能会有问题：

当 max(A, B) 过大时，例如密集 MLP 矩阵，更新变得过小，从而限制了模型的表示能力，导致次优性能；
当 max(A, B) 过小时，例如将 GQA（Shazeer，2019 年）或 MLA（DeepSeek-AI 等人，2024 年）中的每个 KV 头视为单独参数，更新变得过大，导致训练不稳定，性能次优。

在这里插入图片描述

为了在不同形状的矩阵之间保持一致的更新 RMS，我们提出根据 √(max(A, B)) 对每个矩阵的 Muon 更新进行缩放，以抵消引理 1 的影响。第 3.1 节的实验表明，这种策略对优化有益。

匹配 AdamW 的更新 RMS：Muon 被设计为更新基于矩阵的参数。在实践中，AdamW 与 Muon 一起使用，用于处理非矩阵参数，如 RMSNorm、LM 头和嵌入参数。我们希望优化器超参数（学习率 η、权重衰减 λ）可以在矩阵和非矩阵参数之间共享。

我们提出将 Muon 的更新 RMS 调整为与 AdamW 类似。根据经验观察，AdamW 的更新 RMS 通常在 0.2 到 0.4 之间。因此，我们通过以下调整将 Muon 的更新 RMS 缩放到这个范围：

Wt = Wt−1 − ηt(0.2 · Ot · √(max(A, B)) + λWt−1)

我们通过实验证实了这一选择（详见附录 A）。此外，我们强调，通过这种调整，Muon 可以直接重用为 AdamW 调整的学习率和权重衰减。

其他超参数：Muon 还包含两个可调超参数：Newton-Schulz 迭代步数和动量 µ。我们经验证明，当设置 N 为 10 时，迭代过程会比 N = 5 产生更准确的正交化结果，但不会带来更好的性能。因此，为了效率，我们在本工作中设置 N = 5。我们没有看到在调整动量时有持续的性能提升，因此我们选择与 K. Jordan 等人（2024 年）相同的 0.95。

2.3 分布式 Muon

ZeRO-1 和 Megatron-LM：Rajbhandari 等人（2020 年）引入了 ZeRO-1 技术，将昂贵的优化器状态（例如主权重、动量）分布在集群中。Megatron-LM（Shoeybi 等人，2020 年）将 ZeRO-1 整合到其本地并行设计中。基于 Megatron-LM 的复杂并行策略，例如张量并行（TP）、管道并行（PP）、专家并行（EP）和数据并行（DP），ZeRO-1 的通信工作量可以从在整个分布式世界中收集减少到仅在数据并行组中收集。

方法：ZeRO-1 对 AdamW 很高效，因为它以元素级方式计算更新。然而，Muon 需要完整的梯度矩阵来计算更新。因此，原始的 ZeRO-1 不直接适用于 Muon。我们提出了一种基于 ZeRO-1 的新分布式解决方案，称为分布式 Muon。分布式 Muon 遵循 ZeRO-1 在 DP 上划分优化器状态，并引入了两个额外的操作，与原始的 Zero-1 AdamW 优化器相比：
在这里插入图片描述

DP 收集：对于本地 DP 划分的主权重（模型权重的 1/DP 大小），此操作收集相应的划分梯度到一个完整的梯度矩阵。
计算完整更新：在上述收集之后，在完整的梯度矩阵上执行 Newton-Schulz 迭代步骤，如第 2.1 节所述。注意，我们将丢弃完整更新矩阵的其余部分，因为只需保留对应于本地参数的部分即可进行更新。

分布式 Muon 的实现如算法 1 所述。分布式 Muon 引入的额外操作用蓝色标出。

分析：我们在几个方面比较了分布式 Muon 和经典的基于 ZeRO-1 的分布式 AdamW（简称为分布式 AdamW）：

内存使用：Muon 只使用一个动量缓冲区，而 AdamW 使用两个动量缓冲区。因此，Muon 优化器额外使用的内存是分布式 AdamW 的一半。
通信开销：额外的 DP 收集操作是初始梯度 reduce-scatter 操作的反向操作。然而，Muon 只需要在 bf16 中执行 Newton-Schulz 迭代步骤，从而将通信开销减少到 50%。总体而言，分布式 Muon 的通信工作量是分布式 AdamW 的 150%。
延迟：分布式 Muon 的端到端延迟比分布式 AdamW 大，因为它引入了额外的通信并需要运行 Newton-Schulz 迭代步骤。然而，这并不是一个显著的问题，因为（a）只需要大约 5 个 Newton-Schultz 迭代步骤即可获得良好的结果（在第 2.2 节中讨论），（b）由优化器引起的端到端延迟与模型的前向-后向传递时间相比可以忽略不计（例如，通常为 1% 到 3%）。此外，几种工程技巧，如重叠收集和计算，以及重叠优化器 reduce-scatter 与参数收集，可以进一步减少延迟。

在我们的分布式集群中训练大型模型时，分布式 Muon 与 AdamW 对比没有明显的延迟开销。我们很快将为开源的 Megatron-LM（Shoeybi 等人，2020 年）项目提交一个实现分布式 Muon 的 pull request。

3 实验

3.1 一致的更新 RMS

如第 2.2 节所述，我们旨在在所有矩阵参数之间匹配更新 RMS，并与 AdamW 匹配。我们实验了两种方法来控制 Muon 更新 RMS，并将其与仅与 AdamW 保持一致 RMS 的基线进行比较：
在这里插入图片描述

基线：我们将更新矩阵乘以 0.2 · √H（H 是模型隐藏大小），以与 AdamW 保持一致的更新 RMS。注意，对于大多数矩阵，max(A, B) 等于 H。
Wt = Wt−1 − ηt(0.2 · Ot · √H + λWt−1)
更新范数：我们可以直接归一化通过 Newton-Schulz 迭代计算的更新，使其 RMS 严格变为 0.2；
Wt = Wt−1 − ηt(0.2 · Ot / RMS(Ot) + λWt−1)
调整学习率：对于每个更新矩阵，我们可以根据其形状按 0.2 · √(max(A, B)) 的因子缩放其学习率。
Wt = Wt−1 − ηt(0.2 · Ot · √(max(A, B)) + λWt−1)

分析：我们设计了实验来说明 Muon 更新 RMS 在早期训练阶段的影响，因为我们观察到在更大规模训练模型时，意外的行为很快就会发生。我们使用 3.2 节中描述的小型 800M 模型进行实验。当矩阵维度之间的差异增大时，更新 RMS 不一致的问题更加明显。为了突出这个问题以便进一步研究，我们稍微修改了模型架构，将 Swiglu MLP 替换为标准的两层 MLP，将其矩阵参数的形状从 [H, 2.6H] 改为 [H, 4H]。我们在 20B 个标记的训练计划中训练了 4B 个标记后评估了模型的损失，并监控了其一些参数的 RMS，特别是，注意力查询（形状 [H, H]）和 MLP（形状 [H, 4H]）。从表 1 中，我们观察到几个有趣的发现：

更新范数和调整学习率都比基线表现更好；
对于形状为 [H, 4H] 的 MLP 权重矩阵，更新范数和调整学习率获得的权重 RMS 大约是基线的两倍。这是合理的，因为 √(max(H, 4H)) / √H = 2，所以更新范数和调整学习率的更新 RMS 大约是基线的两倍；
对于形状为 [H, H] 的注意力查询权重矩阵，更新范数仍然对更新进行归一化，而调整学习率没有，因为 √(max(H, H)) / √H = 1。因此，调整学习率的结果与基线的权重 RMS 类似，但更新范数的权重 RMS 类似于其 MLP。

基于这些发现，我们选择在未来的实验中使用调整学习率方法，因为它的成本较低。

3.2 Muon 的扩展定律

为了与 AdamW 进行公平比较，我们在 Llama 架构的一系列密集模型上进行了 Muon 的扩展定律实验。AdamW 的超参数通过网格搜索确定，遵循计算最优训练设置。模型架构和超参数的详细信息可以在表 2 中找到。对于 Muon，如第 2.2 节所述，由于我们将 Muon 的更新 RMS 与 AdamW 匹配，我们直接重用了 AdamW 的超参数。

拟合的扩展定律曲线如图 3 所示，拟合方程的详细信息如表 3 所示。如图 1a 所示，Muon 在计算最优设置下仅需要大约 52% 的训练 FLOPs 即可与 AdamW 匹配性能。

3.3 使用 Muon 进行预训练

模型架构：为了评估 Muon 与当代模型架构的对比，我们从头开始使用 deepseek-v3-small 架构进行预训练，因为它表现出强大的性能，并且原始结果可以作为对比参考。我们的预训练模型有 2.24B 个激活参数和 15.29B 个总参数（包括嵌入参数时为 3B 个激活参数和 16B 个总参数）。对架构的 minor 修改详见附录 C。

在这里插入图片描述

预训练数据：我们的预训练数据详细信息可以在 K. Team（2025 年）中找到。预训练期间的最大上下文长度为 8K。

预训练：模型在几个阶段进行训练。我们在第 1 阶段和第 2 阶段使用 1e-3 的 auxfree 偏置更新率，在第 3 阶段使用 0.0 的 auxfree 偏置更新率。所有阶段的权重衰减均设置为 0.1。更多训练细节和讨论详见附录 D。

0 到 33B 个标记：在此阶段，学习率在 2k 步内线性增加到 4.2e-4。批量大小保持在 2048 个样本；
33B 到 5.2T 个标记：在此阶段，学习率以余弦风格从 4.2e-4 衰减到 4.2e-5。我们保持批量大小在 2048 个样本，直到 200B 个标记，然后在剩余训练中加倍到 4096 个样本；
5.2T 到 5.7T 个标记：在此阶段（也称为冷却阶段），学习率在 100 步内增加到 1e-4，然后在线性衰减到 500B 个标记内的 0，我们保持批量大小为 4096 个样本。在此阶段，我们使用最高质量的数据，重点关注数学、代码和推理。

评估基准：我们的评估涵盖四个主要类别的基准，每个类别旨在评估模型的不同能力：
在这里插入图片描述

英语语言理解和推理：MMLU（5-shot）（Hendrycks 等人，2021 年），MMLU-pro（5-shot）（Wang 等人，2024 年），BBH（3-shot）（Suzgun 等人，2022 年），TriviaQA（5-shot）（Joshi 等人，2017 年）
代码生成：HumanEval（pass@1）（Chen 等人，2021 年），MBPP（pass@1）（Austin 等人，2021 年）
数学推理：GSM8K（4-shot）（Cobbe 等人，2021 年）MATH（Hendrycks 等人，2021 年），CMATH（Wei 等人，2023 年）
中文语言理解和推理：C-Eval（5-shot）（Huang 等人，2023 年），CMMLU（5-shot）（Li 等人，2024 年）

性能：我们将使用 Muon 训练的模型命名为“Moonlight”。我们比较了 Moonlight 与在相似规模上训练的不同公共模型。我们首先在 1.2T 个标记处评估 Moonlight，并将其与以下模型进行比较，这些模型具有相同的架构，并使用相似数量的标记进行训练：

Deepseek-v3-Small（DeepSeek-AI 等人，2024 年）是一个 2.4B/16B 参数的 MoE 模型，使用 1.33T 个标记进行训练；
Moonlight-A：遵循与 Moonlight 相同的训练设置，但使用 AdamW 优化器。

在这里插入图片描述

对于 Moonlight 和 Moonlight-A，我们使用了 5.7T 预训练的中间 1.2T 个标记检查点，此时学习率尚未衰减到最小值，模型尚未经过冷却阶段。

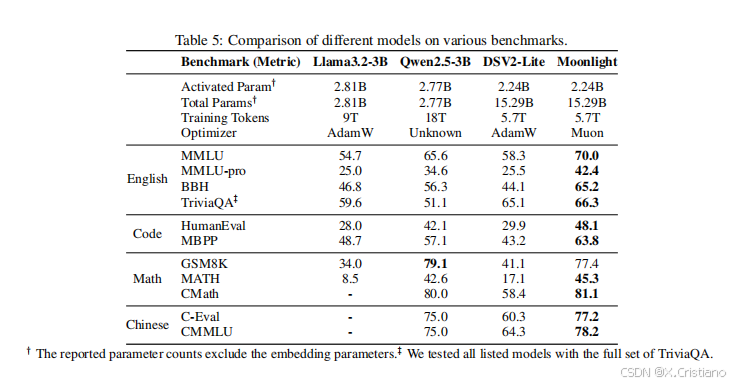
从表 4 中可以看出，Moonlight-A，我们的 AdamW 训练基线模型，在与相似的公共模型对比中表现出色。Moonlight 显著优于 Moonlight-A，证明了 Muon 的扩展有效性。在 Moonlight 完全训练到 5.7T 个标记后，我们将其与在相似规模上训练的公共模型进行了比较，结果如表 5 所示：

LLAMA3-3B（Grattafiori 等人，2024 年）是一个 3B 参数的密集模型，使用 9T 个标记进行训练；
Qwen2.5-3B（Yang 等人，2024 年）是一个 3B 参数的密集模型，使用 18T 个标记进行训练；
Deepseek-v2-Lite（DeepSeek-AI 等人，2024 年）是一个 2.4B/16B 参数的 MOE 模型，使用 5.7T 个标记进行训练。

如表 5 所示，Moonlight 在与使用相似数量标记训练的具有相似架构的模型对比中表现更优。即使与使用大幅更大数据集训练的密集模型相比，Moonlight 仍保持竞争力。Moonlight 的性能进一步与其它知名语言模型在 MMLU 和 GSM8k 上进行了比较，如图 1b 和附录 E 图 8.6 所示。值得注意的是，Moonlight 位于模型性能与训练预算的帕累托前沿，超越了许多其他模型。

在这里插入图片描述

3.4 奇异谱的动态

为了验证 Muon 可以在更多样化的方向上优化权重矩阵的直觉，我们对使用 Muon 和 AdamW 训练的权重矩阵进行了谱分析。对于具有奇异值 σ = (σ1, σ2, · · · , σn) 的权重矩阵，我们计算该矩阵的 SVD 熵如下：

H(σ) = − 1 / log n * Σ(n i=1) (σi² / Σ(n j=1) σj²) * log (σi² / Σ(n j=1) σj²)

如图 4 所示，我们在使用 1.2T 个标记进行预训练期间，对不同训练检查点的权重矩阵的平均 SVD 熵进行了可视化。我们可以看到，在所有训练检查点和所有组的权重矩阵中，Muon 的 SVD 熵均高于 AdamW，这验证了 Muon 可以为权重矩阵提供更多样化更新方向的直觉。这种差异在用于专家选择的路由器权重中更为显著，表明混合专家模型可以从 Muon 中受益更多。

此外，我们在附录 F 中展示了在 1.2T 个标记训练检查点处每个权重矩阵的奇异值分布。我们发现，对于超过 90% 的权重矩阵，使用 Muon 优化的 SVD 熵高于使用 AdamW 优化的 SVD 熵，为 Muon 在探索多样化优化方向方面的优越能力提供了强有力的实证证据。

3.5 使用 Muon 进行监督微调（SFT）

在本节中，我们展示了在 LLM 训练的标准 SFT 阶段中 Muon 优化器的消融研究。我们的发现表明，Muon 引入的好处在 SFT 阶段仍然存在。具体而言，一个既使用 Muon 进行预训练又使用 Muon 进行微调的模型在消融研究中优于其他模型。然而，我们也观察到，当 SFT 优化器与预训练优化器不同时，使用 Muon 进行 SFT 并未显示出比 AdamW 显著的优势。这表明仍有相当大的空间可供进一步探索，我们将其留作未来的工作。

3.5.1 预训练和 SFT 优化器互换性的消融研究

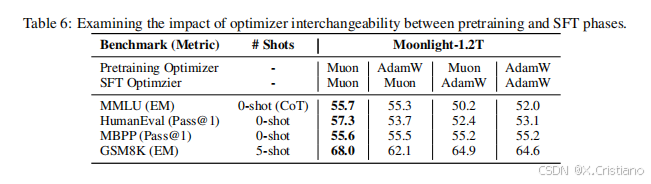
为了进一步研究 Muon 的潜力，我们使用 Muon 和 AdamW 优化器对 Moonlight@1.2T 和 Moonlight-A@1.2T 进行了微调。这些模型在开源的 tulu-3-sft-mixture 数据集（Lambert 等人，2024 年）上进行了两个 epoch 的微调，该数据集包含 4k 序列长度的数据。学习率遵循线性衰减计划，从 5 × 10−5 开始，逐渐减少到 0。表 6 中的结果突显了 Moonlight@1.2T 相比 Moonlight-A@1.2T 的优越性能。
在这里插入图片描述

3.5.2 使用 Muon 对公共预训练模型进行 SFT

我们进一步将 Muon 应用于公共预训练模型的监督微调，特别是 Qwen2.5-7B 基础模型（Yang 等人，2024 年），使用开源的 tulu-3-sft-mixture 数据集（Lambert 等人，2024 年）。该数据集以 8k 序列长度打包，我们采用了余弦衰减学习率计划，从 2 × 10−5 开始，逐渐减少到 2 × 10−6。结果如表 7 所示。为了进行比较，我们表明，使用 Muon 微调的模型在性能上与使用 Adam 微调的模型相当。这些结果表明，为了获得最佳性能，最好在预训练阶段应用 Muon 而不是在监督微调阶段。
在这里插入图片描述

4 讨论

有几个可能的研究方向可以进一步探索和扩展当前的发现。

将所有参数纳入 Muon 框架：目前，Muon 优化器与 Adam 优化器结合使用，某些参数仍由 Adam 优化。这种混合方法虽然可行，但存在改进的空间。将所有参数的优化完全纳入 Muon 框架是一个重要的研究课题。
将 Muon 扩展到 Schatten 范数：Muon 优化器可以被解释为在谱范数下的最陡下降方法。鉴于 Schatten 范数的广泛适用性和灵活性，将 Muon 扩展到涵盖一般的 Schatten 范数是一个有前景的方向。这种扩展可能会解锁额外的优化能力，并可能比当前基于谱范数的实现获得更好的结果。
理解和解决预训练-微调不匹配问题：实践中观察到的一个显著现象是，使用 AdamW 预训练的模型在使用 Muon 微调时性能不佳，反之亦然。这种优化器不匹配构成了有效利用大量 AdamW 预训练检查点的显著障碍，需要进行严格的理论研究。精确理解其背后的机制对于制定 robust 和有效的解决方案至关重要。

5 结论

在本技术报告中，我们对 Muon 在 LLM 训练中的可扩展性进行了全面研究。通过系统的分析和改进，我们成功地将 Muon 应用于一个在 5.7 万亿个标记上训练的 3B/16B 参数 MoE 模型。我们的结果表明，Muon 可以有效地取代 AdamW，成为大规模 LLM 训练的标准优化器，在训练效率和模型性能方面提供了显著的优势。通过开源我们的实现、Moonlight 模型和中间训练检查点，我们旨在促进可扩展优化技术的进一步研究，并加速 LLMs 训练方法的发展。