折射与反射
光线与光学元件相互作用,无非只有两件事,反射和透射。而就目前看来,我们所常用的光学元件,也无非有两种表面,即平面和球面,二维化之后就简化成了射线与线段,射线与劣弧的关系。
平面反射
无论从哪个角度来看,平面的反射折射都要比球面更简单,而反射问题要比折射问题更简单,所以,我们首先处理平面的反射问题。
反射定律即入射角等于反射角,心念及此,最为循规蹈矩的思路必然是先找到入射光线和平面的夹角,然后用这个夹角和平面(在二维空间中是一条直线)在空间中的斜率,由这个斜率与入射角得到出射光的斜率,然后就可以得到出射光的方程。
这个方法的问题是需要反复使用三角函数和反三角函数,而三角函数和反三角函数并非严格意义上的互为相反,所以在传参的过程中,可能会遇到一些麻烦。
相对来说,比较不容易出错的方法是,寻找入射点关于法线的对称点,那么这个对称点与交点的连线,便是出射光的方程。
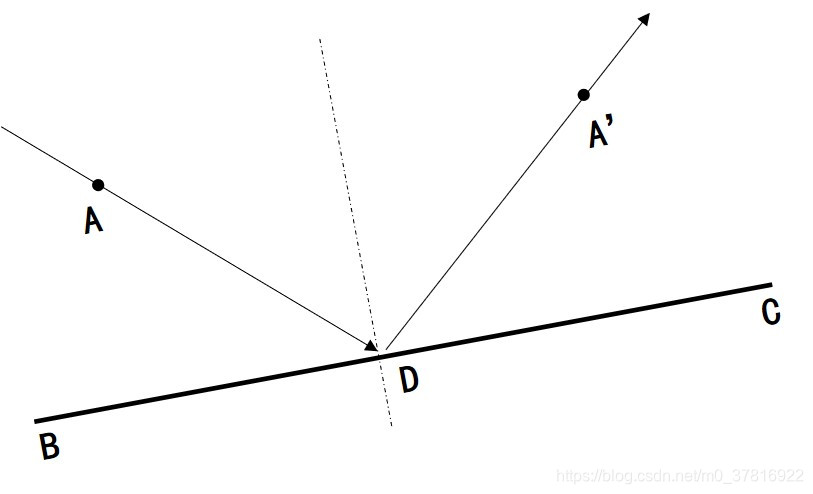
如图所示,设入射光的方程为
a
0
x
+
b
0
y
+
c
0
=
0
a_0x+b_0y+c_0=0
a0x+b0y+c0=0,设反射面BC的方程为
a
1
x
+
b
1
+
c
1
=
0
a_1x+b_1+c_1=0
a1x+b1+c1=0。则二者交点
(
x
,
y
)
(x,y)
(x,y)即是如下方程组的解。
[
a
1
b
1
a
2
b
2
]
⋅
[
x
y
]
=
[
c
1
c
2
]
\left[ \begin{matrix}a_1&b_1\\a_2&b_2\end{matrix}\right]\cdot\left[\begin{matrix}x\\y\end{matrix}\right] =\left[\begin{matrix}c_1\\c_2\end{matrix}\right]
[a1a2b1b2]⋅[xy]=[c1c2]
若接触D点的坐标为 ( x D , y D ) (x_D,y_D) (xD,yD),则法线方程为 − b 1 x + a 1 y + c = 0 -b_1x+a_1y+c=0 −b1x+a1y+c=0,又因D点过法线,则有
− b 0 x D + a 0 y D + c = 0 → c = a 0 y D − b 0 x D -b_0x_D+a_0y_D+c=0 \to c=a_0y_D-b_0x_D −b0xD+a0yD+c=0→c=a0yD−b0xD
为方便起见,现将法线表示为
a
x
+
b
y
+
c
=
0
ax+by+c=0
ax+by+c=0,A点坐标为
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1),设其对称点为
(
x
2
,
y
2
)
(x_2,y_2)
(x2,y2),则二者满足关系:
{
a
⋅
x
1
+
x
2
2
+
b
⋅
y
1
+
y
2
2
+
c
=
0
y
2
−
y
1
x
2
−
x
1
⋅
(
−
a
b
)
=
−
1
\left\{\begin{aligned} &a\cdot\frac{x_1+x_2}{2}+b\cdot\frac{y_1+y_2}{2}+c=0\\ &\frac{y_2-y_1}{x_2-x_1}\cdot(-\frac{a}{b})=-1 \end{aligned}\right.
⎩⎪⎨⎪⎧a⋅2x1+x2+b⋅2y1+y2+c=0x2−x1y2−y1⋅(−ba)=−1
整理得
[
b
−
a
a
b
]
⋅
[
x
1
y
1
]
=
∣
b
x
2
−
a
y
2
−
2
c
−
a
x
2
−
b
y
2
∣
\left[\begin{matrix}b&-a\\a&b\end{matrix}\right]\cdot\left[\begin{matrix}x_1\\y_1\end{matrix}\right] =\begin{vmatrix}bx_2-ay_2\\-2c-ax_2-by_2\end{vmatrix}
[ba−ab]⋅[x1y1]=∣∣∣∣bx2−ay2−2c−ax2−by2∣∣∣∣
解得
{
x
1
=
−
2
a
c
−
2
a
b
y
2
+
(
b
2
−
a
2
)
x
2
a
2
+
b
2
y
1
=
−
2
b
c
−
2
a
b
x
2
+
(
a
2
−
b
2
)
y
2
a
2
+
b
2
\left\{ \begin{aligned} x_1=\frac{-2ac-2aby_2+(b^2-a^2)x_2}{a^2+b^2}\\ y_1=\frac{-2bc-2abx_2+(a^2-b^2)y_2}{a^2+b^2} \end{aligned}\right.
⎩⎪⎪⎨⎪⎪⎧x1=a2+b2−2ac−2aby2+(b2−a2)x2y1=a2+b2−2bc−2abx2+(a2−b2)y2
平面折射
折射与反射的思路如出一辙,最原始的想法仍旧是获取入射角,然后根据折射定律求出射角,然后再按照出射角解出出射光的表达式。这个思路的难点仍旧在三角函数与反函数的转化上。
众所周知,折射定律的表达式为 n 1 s i n θ 1 = n 2 s i n θ 2 n_1sin\theta_1=n_2sin\theta_2 n1sinθ1=n2sinθ2,这个表达式的关键并不在于透射,而在于折射率的变化。如果光在某个表面反射的同时,介质折射率同时发生了突变,如图所示,那么理应同样满足这个关系。

其中,AD为入射光线,DB为出射光线,CD左侧的折射率为
n
1
n_1
n1,右侧为
n
2
n_2
n2。令入射角为
θ
1
\theta_1
θ1,出射角为
θ
2
\theta_2
θ2,则易得
n
1
s
i
n
θ
1
=
n
2
s
i
n
θ
2
→
n
1
⋅
l
1
d
1
=
n
2
⋅
l
2
d
2
n_1sin\theta_1=n_2sin\theta_2 \to n1\cdot\frac{l_1}{d_1}=n2\cdot\frac{l_2}{d_2}
n1sinθ1=n2sinθ2→n1⋅d1l1=n2⋅d2l2
可解得
l
2
=
h
(
n
2
n
1
)
2
⋅
[
1
+
(
h
l
1
)
2
]
−
1
l_2=\frac{h}{\sqrt{(\frac{n_2}{n_1})^2\cdot[1+(\frac{h}{l_1})^2]-1}}
l2=(n1n2)2⋅[1+(l1h)2]−1h
则
λ
=
l
2
l
1
=
h
(
n
2
n
1
)
2
⋅
(
l
1
2
+
h
2
)
−
1
\lambda=\frac{l_2}{l_1}=\frac{h}{\sqrt{(\frac{n_2}{n_1})^2\cdot(l_1^2+h^2)-1}}
λ=l1l2=(n1n2)2⋅(l12+h2)−1h
至此,我们发现折射与反射在表达形式上是相通的,如果令入射点关于法线做垂线,垂足为C,约定这条垂线与出射光线的交点为出射点B,那么出射点到垂足的距离BC与入射点到垂足的距离AC之间是满足比例关系的。当入射光线和反射光线的折射率相等时,这个比例为1,否则比例为 λ \lambda λ。
我们还能发现,这个 λ \lambda λ不一定有解,因为分母中有一个根号表达式,当内部的值小于0时,自然无解。这与我们的物理直觉是符合的,即并不是所有的入射光线都有折射光线,当折射光线消失的时候,就发生了全反射。
所以,当务之急是根据入射点找垂足,易得
{
a
x
+
b
y
+
c
=
0
−
b
x
+
a
y
+
b
x
0
−
a
y
0
=
0
→
{
x
=
b
2
x
0
−
a
b
y
0
−
a
c
a
2
+
b
2
y
=
a
2
y
0
−
a
b
x
0
−
b
c
a
2
+
b
2
\left\{\begin{aligned} &ax+by+c=0\\ &-bx+ay+bx_0-ay_0=0 \end{aligned}\right. \to\left\{\begin{aligned} &x=\frac{b^2x_0-aby_0-ac}{a^2+b^2}\\ &y=\frac{a^2y_0-abx_0-bc}{a^2+b^2} \end{aligned}\right.
{ax+by+c=0−bx+ay+bx0−ay0=0→⎩⎪⎪⎨⎪⎪⎧x=a2+b2b2x0−aby0−acy=a2+b2a2y0−abx0−bc
然后根据入射点、垂足以及比例关系,求解出射点,其中,入射点为
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1),垂足为
(
x
,
y
)
(x,y)
(x,y)。
{
x
=
x
1
+
λ
x
2
1
+
λ
y
=
y
1
+
λ
y
2
1
+
λ
→
{
x
2
=
(
1
+
λ
)
x
−
x
1
λ
y
2
=
(
1
+
λ
)
x
−
y
1
λ
\left\{\begin{aligned} &x=\frac{x_1+\lambda x_2}{1+\lambda}\\ &y=\frac{y_1+\lambda y_2}{1+\lambda} \end{aligned}\right. \to\left\{\begin{aligned} &x_2=\frac{(1+\lambda)x-x1}{\lambda} \\ &y_2=\frac{(1+\lambda)x-y1}{\lambda} \end{aligned}\right.
⎩⎪⎪⎨⎪⎪⎧x=1+λx1+λx2y=1+λy1+λy2→⎩⎪⎪⎨⎪⎪⎧x2=λ(1+λ)x−x1y2=λ(1+λ)x−y1
那么对于我们所熟知的折射问题,即可令入射点关于反射平面做一次对称,再关于发现做一次定比延长线的对称,即可得到出射点。
python实现
至此,我们已经完全建立了一套反射与折射的关系,代码如下:
#得到点关于直线的对称点,k为比例系数
def getSymDot(point,line,k=1):
return tuple((np.array(getPedal(point,line))*(1+k)-point)/k)
#得到直线的垂足
def getPedal(point,line):
a,b,c=line
x0,y0 = point
y1 = (a**2*y0-a*b*x0-b*c)/(a**2+b**2)
x1 = (b**2*x0-a*b*y0-a*c)/(a**2+b**2)
return (x1,y1)
函数getSymDot即通过输入点和线来求解对称点,其思路是把点关于线对称的问题转化为点关于垂足对称的问题。所以引用了getPedal函数,这个函数通过输入一点和线来返回过点做线的垂线所得到的垂足。
所有代码都是对上述数学公式的简单复现。
def cataDioLine(abc=[1,-1,1],line=[2,-1,1],
sPoint=[],cross=[],n1=1,n2=1.5):
normal = [-line[1],line[0],line[1]*cross[0]-line[0]*cross[1]]#法线
flecDot = getSymDot(sPoint,normal)
flec=getABC([cross,flecDot])
dPara = np.sqrt(line[0]**2+line[1]**2)
dNormal = np.abs(np.array(normal).dot(list(sPoint)+[1]))/dPara#到法线距离
dPane = np.abs(np.array(line).dot(list(sPoint)+[1]))/dPara#到反射面距离
if dNormal == 0:
return flec,abc
delt = (n2/n1)**2*(1+(dPane/dNormal)**2)-1#判定全反射
if delt>0:
k =dPane/dNormal/np.sqrt(delt)
fracDot = getSymDot(sPoint,normal,k)
fracDot = getSymDot(fracDot,line)
frac = getABC([cross,fracDot])
return flec,frac
return flec,[0,0,0]
函数cataDioLine则是反射折射的实现函数。注意,在此引入的getABC并不是此前定义的通过点和角度求表达式的函数,而是通过两点转[a,b,c]的函数。
那么我们是否可以写一个同名函数来实现不同的功能呢?很遗憾的是,Python不支持函数的重载,所以只能将同名函数封装在一起:
def getABC(*par):
if len(par)==1: #此时传入的参数为点对dots=[(x0,y0),(x1,y1)]
dots = par[0]
abc = [dots[1][1]-dots[0][1],
dots[0][0]-dots[1][0],
-np.linalg.det(dots)]
return np.array(abc)/(np.sqrt(abc[0]**2+abc[1]**2))
elif len(par)==2: #此时传入的参数为点和角度(x0,y0),theta
theta,sPoint = par
a,b = [np.sin(theta),-np.cos(theta)]
c = -(a*sPoint[0]+b*sPoint[1])
return [a,b,c]
看到输入参数(*par),我们很多人可能会产生某些不是很美妙的联想,但不要兴奋,这只是python的一种传参方式。(*args)表示将传入的参数组成一个列表args;(**kargs)表示将传入的参数组成一个字典kargs。
弧面问题
光线在弧面上的反射问题,是典型的那种看似复杂实则简单的纸老虎问题,简单到我们只要找到法线就能轻松地转化为平面问题。
所以,问题被简单地转化为求解圆的切线问题——这个切线即反射平面。由于数学过程过于简单,就不写公式了,读者可以试着看代码反推公式。
#获取过交点的圆弧的切线
def getTangent(corss=[0,1],circle=[0,0,1]):
a = corss[0]-circle[0]
b = corss[1]-circle[1]
c = -a*corss[0]-b*corss[1]
return [a,b,c]
至此,我们就可以得到一个完整的折射反射问题的求解方案:
#光在直线或弧线表面的反折射
def cataDio(abc=[1,-1,1],dots=[(0,2),(2,2)],
sPoint=[-2,-1],n1=1,n2=1.5):
cross = getCross(abc,dots,sPoint) #获取交点
if cross == []:
return [],[],[]
if len(dots)==3:
line = getTangent(cross,arc2cir(dots)) #圆上切线
elif len(dots)==2:
line = getABC(dots)
flec,frac = cataDioLine(abc,line,sPoint,cross,n1,n2)
return cross,flec,frac
当然,这里的getCross也需要重新写成不仅适合直线,而且适合弧线的形式:
def getCross(abc=[1,-1,0],dots=[[0,-1],[0,1],[0.5,0]],point=[]):
if len(dots)==3:
return getCrossArc(abc,dots,point)
if len(dots)==2:
return getCrossDots(abc,dots,point)
这时我们发现用两个点表示线段,三个点表示弧线还是比较舒服的一种做法,至少二者在表达形式上的统一似乎能为我们带来某种内心的愉悦。

























 1152
1152

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










