牛顿法至少有两个应用方向,1、求方程的根,2、最优化
1:求方程的根
原理是利用泰勒公式,在x0处展开,且展开到一阶,即f(x) = f(x0)+(x-x0)f’(x0)
求解方程f(x)=0,
即:
f(x0)+(x-x0)f’(x0)=0,
x = x1=x0-f(x0)/f’(x0),
因为这是利用泰勒公式的一阶展开,f(x) = f(x0)+(x-x0)f’(x0)处并不是完全相等,而是近似相等,这里求得的x并不能让f(x)=0,只能说f(x)的值比f(x0)更接近f(x)=0,于是乎,迭代求解的想法就很自然了,可以进而推出x(n+1)=x(n)-f(x(n))/f’(x(n)),通过迭代,这个式子必然在f(x)=0的时候收敛。整个过程如下图:

2:牛顿法求极值
对函数f(x)进行二阶泰勒展开
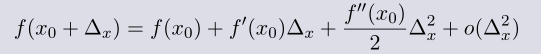
这里把前三项看作关于
Δ
x
的
二
次
函
数
g
(
Δ
x
)
,
对
该
函
数
求
导
获
得
函
数
的
极
值
点
有
\Delta_x 的二次函数g(\Delta_x ),对该函数求导获得函数的极值点有
Δx的二次函数g(Δx),对该函数求导获得函数的极值点有
f
′
′
(
x
0
)
Δ
x
+
f
′
(
x
0
)
=
0
f''(x_0)\Delta_x+f'(x_0)=0
f′′(x0)Δx+f′(x0)=0
f
′
′
(
x
0
)
(
x
−
x
0
)
+
f
′
(
x
0
)
=
0
f''(x_0)(x-x_0)+f'(x_0)=0
f′′(x0)(x−x0)+f′(x0)=0
x
−
x
0
=
−
f
′
(
x
0
)
f
′
′
(
x
0
)
x-x_0=-\frac{f'(x_0)}{f''(x_0)}
x−x0=−f′′(x0)f′(x0)
x
=
x
0
−
f
′
(
x
0
)
f
′
′
(
x
0
)
x=x_0-\frac{f'(x_0)}{f''(x_0)}
x=x0−f′′(x0)f′(x0)
当
x
0
x_0
x0是多变量时,定义一阶导数雅可比矩阵为
J
f
(
X
n
)
J_f(X_n)
Jf(Xn)
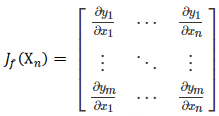
二阶导数为Hessian矩阵

牛顿法 演变为:
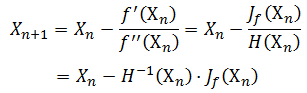






















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








