SVM(支持向量机)

svm分类：

• 硬间隔 svm(hard margin)
• 软间隔 svm(soft margin)
• 核间隔 svm(kernal margin)
  特点：
  SVM 有三宝：间隔，对偶，核技巧

SVM分类思想：找到一个超平面，使得该超平面能够正确分割样本，并满足最大化margin分类器,也叫最大化间隔分类器

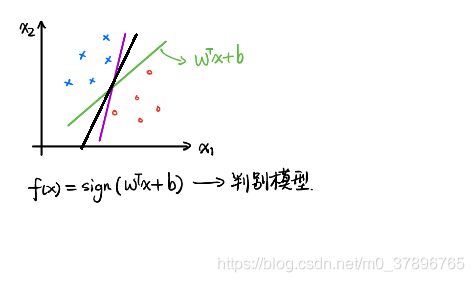
数学描述：
$y=sign(w^{T}x+b)，当w^{T}x+b>0时，y=1,w^{T}x+b<0时，y=-1$
所以原函数可以描述为如下不等式
$y(w^{T}x+b)>0$

间距函数用distance(x)表示，我们知道点到直线距离公式：

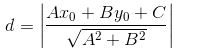
这里点到超平面$w^{T}x+b$的距离为：

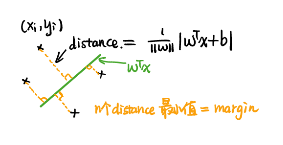
margin分类器定义：点到超平面的最小距离
margin分类器数学描述：
$mindistance(x_i)=min(\frac{1}{||w||}|w^T{x}_i+b|)$

最大化margin分类器可以描述为：
$max\min distance(x_i)=max\min (\frac{1}{||w||}|w^T{x}_i+b|)$
$=max\frac{1}{||w||}\min (|w^T{x}_i+b|)$
由于$|w^T{x}_i+b|$是绝对值函数，这里可以用$y_i(w^T{x}_i+b)$代替
所以原问题可以描述为下列优化问题：
$max\frac{1}{||w||}min{y}_i(w^T{x}_i+b)$
$s.t.y_i(w^T{x}_i+b)>0$
令$min{y}_i(w^T{x}_i+b)=1$
$max\frac{1}{||w||}等价于：$ $min||w||$
等价于：$min\frac{1}{2}{w}^2$

这时原问题可以描述为
$max\frac{1}{||w||}=min\frac{1}{2}{w}^{T}w$
$s.t.1-y_i(w^T{x}_i+b)\le 0$
此时的问题是凸优化问题，可以采样拉格郎日对偶方式处理
问题的拉格朗日函数：
$L(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i(1-y_i(w^T{x}_i+b))$
拉格郎日对偶函数为
$g(\lambda )=\underset{w,b}{\min }(L(w,b,\lambda ))$
对偶问题描述为：
$\{\begin{array}{l}maxg(\lambda )=\underset{\lambda }{\max }\underset{w,b}{\min }(L(w,b,\lambda ))\\ \lambda \ge 0\end{array}$

$maxg(\lambda )=\underset{\lambda }{\max }\underset{w,b}{\min }(w^{T}w+\sum _{i=1}^n{\lambda }_i(1-y_i(w^T{x}_i+b)))$

先求$\min L(w,b,\lambda )$

对b求偏导
$\frac{\partial L(w,b,\lambda )}{b}=-\sum _{i=1}^n{\lambda }_i{y}_i=0$
展开拉格郎日函数有
$L(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i(1-y_i{w}^T{x}_i-y_{i}b)$
$=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i-\sum _{i=1}^n{\lambda }_i{y}_i{w}^T{x}_i-\sum _{i=1}^n{\lambda }_i{y}_{i}b$
$=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i-\sum _{i=1}^n{\lambda }_i{y}_i{w}^T{x}_i$
对w求偏导：
$\frac{\partial L(w,b,\lambda )}{w}=w-\sum _{i=1}^n{\lambda }_i{y}_i{x}_i=0$
$w=\sum _{i=1}^n{\lambda }_i{y}_i{x}_i$
带入原函数有：
$L(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i-\sum _{i=1}^n{\lambda }_i{y}_i{w}^T{x}_i$
$=\frac{1}{2}(\sum _{i=1}^n{\lambda }_i{y}_i{x}_i{)}^T(\sum _{j=1}^n{\lambda }_j{y}_j{x}_j)+\sum _{i=1}^n{\lambda }_i-\sum _{i=1}^n{\lambda }_i{y}_i(\sum _{j=1}^n{\lambda }_j{y}_j{x}_j{)}^T{x}_i$
$=-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^n{\lambda }_i$

$maxg(\lambda )=max(-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^n{\lambda }_i)$

于是有下列对偶优化问题：
$\{\begin{array}{l}\min g(\lambda )=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^n{\lambda }_i\\ \lambda \ge 0\\ \sum _{i=1}^n{\lambda }_i{y}_i=0\end{array}$

由于原问题是凸问题，满足staler 条件，所以满足强对偶关系，也就是原问题最优解=对偶问题最优解，
从而也满足KKT条件:
$\{\begin{array}{l}1-y_i(w^T{x}_i+b)\le 0原问题满足约束\\ \\ {\lambda }_i\ge 0对偶问题满足约束\\ \\ {\lambda }_i(1-y_i{w}^T{x}_i-y_{i}b)=0互补松弛\\ \\ \frac{\partial L(w,b,\lambda )}{b}=0,\frac{\partial L(w,b,\lambda )}{w}=0,\frac{\partial L(w,b,\lambda )}{\lambda }=0\end{array}$

令$1-y_i{w}^T{x}_i-y_{i}b=0，有y_{i}b=1-y_i{w}^T{x}_i$
两边同时乘以$y_i有b=y_i-w^t{x}_i=y_i-\sum _{i=1}^n{\lambda }_i{y}_i{x}_i^T{x}_i$
也就是最优的w,b满足
$w^{\ast }=\sum _{i=1}^n{\lambda }_i{y}_i{x}_i$
$b^{\ast }=y_i-w^t{x}_i=y_i-\sum _{i=1}^n{\lambda }_i{y}_i{x}_i^T{x}_i$