卡尔曼滤波

1：卡尔曼滤波是一种线性动态模型，

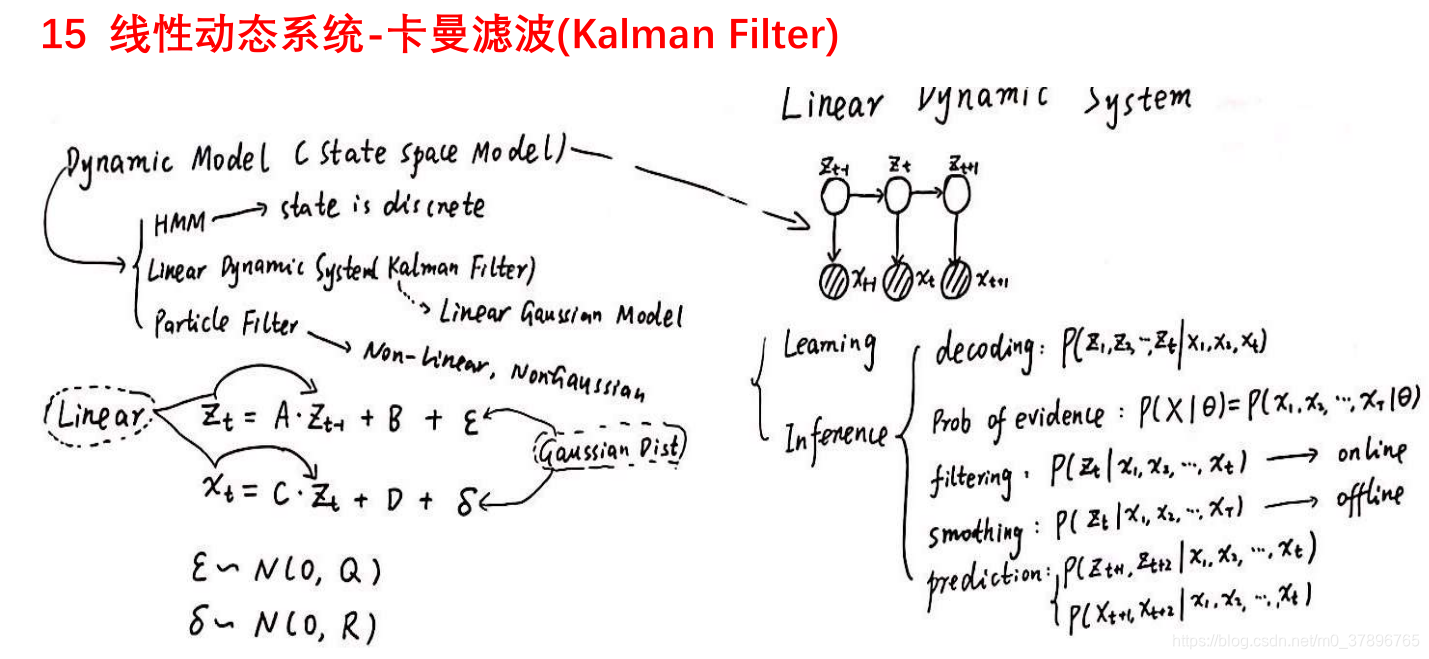
针对的也是有隐状态 和观测状态的模型,和HMM不同的是：
卡尔曼滤波不要求隐状态是离散的，并且前一个状态和后一个状态满足线性关系，也叫线性高斯模型，噪声服从正态分布

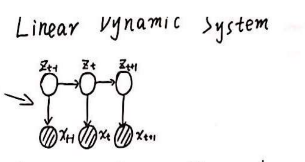
前提条件也符合HMM的前提假设条件：

• 齐次马尔科夫假设
• 观测独立假设
  公式满足：
  
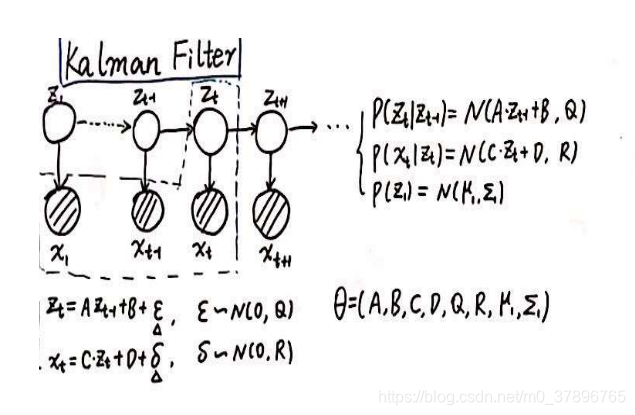
  卡尔曼滤波属于推断问题的一种，已知$x_1,x_2,x_3,..x_t$时刻的观测状态，求$z_t隐状态的概率：$
  $p(z_t|x_1,x_2,..x_t)$
  公式推导：
  $p(z_t|x_1,x_2,..x_t)=\frac{p(z_t,x_1,x_2,..x_t)}{p(x_1,x_2,..x_t)}$
  由于$p(x_1,x_2,..x_t)$可以直接求出，和$z_t$没有关系，这里可以视作常量
  $=\frac{1}{C}\ast p(x_1,x_2,..x_t,z_t)$
  吸出$x_t$
  $=\frac{1}{C}\ast p(x_t|x_1,x_2,..x_{t-1},z_t)p(x_1,x_2,..x_{t-1},z_t)$
  应用观测独立假设和贝叶斯公式
  $=\frac{1}{C}\ast p(x_t|z_t)p(z_t|x_1,x_2,..x_{t-1})p(x_1,x_2,..x_{t-1})$
  这里$p(x_1,x_2,..x_{t-1})$也可以作为常量处理
  $=\frac{1}{C}\ast p(x_t|z_t)p(z_t|x_1,x_2,..x_{t-1})$
  应用联合分布和边缘分布关系
  $=\frac{1}{C}\ast p(x_t|z_t){\int }_{z_{t-1}}p(z_{t-1},z_t|x_1,x_2,..x_{t-1})d{z}_{t-1}$
  $=\frac{1}{C}\ast p(x_t|z_t){\int }_{z_{t-1}}p(z_t|x_1,x_2,..x_{t-1},z_{t-1})p(z_{t-1}|x_1,x_2,..x_{t-1})d{z}_{t-1}$
  应用齐次马尔科夫假设：
  $=\frac{1}{C}\ast p(x_t|z_t){\int }_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_1,x_2,..x_{t-1})d{z}_{t-1}$
  可以看到 $p(z_{t-1}|x_1,x_2,..x_{t-1})是t-1时刻的卡尔曼滤波$

通常记作：
$Bel(z_t)=\frac{1}{C}\ast p(x_t|z_t)\overline{Bel(z_t)}$ 叫做更新过程，也叫修正过程

$\overline{Bel(z_t)}={\int }_{z_{t-1}}p(z_t|z_{t-1})Bel(z_{t-1})d{z}_{t-1}$ 叫做预测过程

2：正态分布：
一元正态分布：
$$\begin{array}{l}p(x)\sim N(\mu ,{\sigma }^2):\\ p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{1}{2}\frac{{(x-\mu )}^2}{{\sigma }^2}}\end{array}$$
多元正态分布：
$$\begin{array}{l}p(x)\sim \mathrm{N}(\mu ,\Sigma ):\\ p(x)=\frac{1}{{(2\pi )}^{n/2}{|\Sigma |}^{1/2}}{e}^{-\frac{1}{2}{(x-\mu )}^t{\Sigma }^{-1}(x-\mu )}\end{array}$$
其中$\mu \in R^n,\Sigma \in R^{n\ast n}是半正定方差矩阵，\left|\Sigma \right|表示方差矩阵的行列式$

3：正态分布的特点：一代高斯，代代高斯

首先，高斯变量线性变换后，仍为高斯分布，均值和方差如下：
$$\begin{array}{l}X\sim N(\mu ,\Sigma )\\ Y=AX+B\end{array}\}\Rightarrow Y\sim N(A\mu +B,A\Sigma A^T)$$
其次：两个高斯的线性组合仍然是高斯分布
$$\begin{array}{l}{X}_1\sim N({\mu }_1,{\sigma }_1^2)\\ X_2\sim N({\mu }_2,{\sigma }_2^2)\end{array}\}\Rightarrow k_1{X}_1+k_2{X}_2+c\sim N\left(k_1{\mu }_1+k_2{\mu }_2+c,k_1^2{\sigma }_1^2+k_2^2{\sigma }_2^2\right)$$
最后，两个相互独立的高斯变量的乘积，仍然为高斯分布，均值和方差如下：
$$\begin{array}{l}{X}_1\sim N({\mu }_1,{\sigma }_1^2)\\ X_2\sim N({\mu }_2,{\sigma }_2^2)\end{array}\}\Rightarrow p(X_1)\cdot p(X_2)\sim N\left(\frac{{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}{\mu }_1+\frac{{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_2^2}{\mu }_2,\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2+{\sigma }_2^2}\right)$$

4: Kalman滤波:
状态方程：$z_t=A{z}_{t-1}+B{u}_t+{\epsilon }_t$
观测方程：$x_t=H{z}_t+{\delta }_t$
其中：
${\epsilon }_t\sim N(0,R_t)$
${\delta }_t\sim N(0,Q_t)$
$z_0\sim N({\mu }_0,P_t)$
应用正态分布线性变换的特点有：
$p(x_t|z_t)\sim N(H{z}_t,Q_t)$
$p(z_t|z_{t-1})\sim N(A{z}_{t-1}+B{u}_t,R_t)$
$p_t=A{P}_{t-1}{A}^T+R_t$

$z_t:是t时刻的状态，是n维向量$
$A_t：是n\ast n状态转移矩阵（在没有输入的影响下）$
$B_t：是n\ast n矩阵（表示u_t如何影响z_t）$
$u_t：是t时刻输入向量$
$x_t：是t时刻观测向量,m维向量$
$H_t：是m\ast n发射概率矩阵（z_t-->x_t）$
$R_t：是n\ast n矩阵，表示隐状态噪声{\epsilon }_t的方差矩阵$
$Q_t：是m\ast m矩阵，表示观测状态噪声{\delta }_t的方差矩阵$
$P_t：是n\ast n矩阵，表示t时刻隐状态z_t的方差矩阵$

5:Kalman滤波算法的推导
1）：系统初始状态
$Bel(z_0)=p(z_0|x_0)\sim N({\mu }_0,P_0)$
2）：预测过程的推导，这里列出预测过程公式：
$\overline{Bel(z_t)}={\int }_{z_{t-1}}p(z_t|z_{t-1})Bel(z_{t-1})$
因为：
$p(z_t|z_{t-1})\sim N(A{z}_{t-1}+B{u}_t,R_t)$
$Bel(z_{t-1})\sim N({\mu }_{t-1},P_{t-1})$
所以：
$\overline{Bel(z_t)}={\int }_{z_{t-1}}p(z_t|z_{t-1})Bel(z_{t-1})$
$={\int }_{z_{t-1}}\frac{1}{{(2\pi )}^{n/2}{|{\mathbb{R}}_t|}^{1/2}}{e}^{-\frac{1}{2}{(z_t-A{z}_{t-1}-B{u}_t)}^t{R_t}^{-1}(z_t-A{z}_{t-1}-B{u}_t)}\ast \frac{1}{{(2\pi )}^{n/2}{|P_t|}^{1/2}}{e}^{-\frac{1}{2}{(z_{t-1}-{\mu }_{t-1})}^t{P_t}^{-1}(z_{t-1}-{\mu }_{t-1})}d{z}_{t-1}$

因为状态方程满足线性关系
所以有：均值更新满足
${\mu }_t=A{\mu }_{t-1}+B{u}_t$
方差矩阵更新满足：
$P_t=A_t{P}_{t-1}{A}^{}$
3）更新过程的推导

$Bel(z_t)=\frac{1}{C}\ast p(x_t|z_t)\overline{Bel(z_t)}$

$$\begin{array}{l}bel(z_t)=\frac{1}{C}p(x_t|z_t)\overline{bel}(z_t)\\ \Downarrow \Downarrow \\ \sim N\left(H_t{x}_t,Q_t\right)\sim N\left({\overline{\mu }}_t,{\overline{P}}_t\right)\\ \Downarrow \\ bel(z_t)=\frac{1}{C}\exp \left\{-\frac{1}{2}{(x_t-H_t{z}_t)}^T{Q}_t^{-1}(x_t-H_t{z}_t)\right\}\exp \left\{-\frac{1}{2}{(z_t-{\bar{\mu }}_t)}^T{\bar{P}}_t^{-1}(z_t-{\bar{\mu }}_t)\right\}\end{array}$$
均值和方差的迭代公式满足(这个不知道咋推导的 ^^)
$$bel(x_t)=\{\begin{array}{l}{\mu }_t={\bar{\mu }}_t+K_t(z_t-H_t{\bar{\mu }}_t)\\ P_t=(I-K_t{H}_t){\overline{P}}_t\end{array}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{K}_t={\overline{P}}_t{H}_t^T(H_t{\overline{P}}_t{H}_t^T+Q_t{)}^{-1}$$