
1.背景知识
在马尔可夫链中:当智能体从一个状态 s s s,选择动作 a a a,会进入另外一个状态 s ′ s' s′;同时,也会给智能体奖励 r r r。
奖励有正有负。“正” 代表我们鼓励智能体在这个状态下继续这么做;“负” 代表我们并不希望智能体这么做。在强化学习中,我们会用奖励 r r r 作为智能体学习的引导,期望智能体获得尽可能多的奖励。
但更多的时候,我们并不能单纯地只通过 r r r 来衡量一个动作的好坏,我们必须用长远的眼光来看待问题。
以考前玩游戏or复习为例:玩游戏会感到快乐,奖励+10;复习会觉得苦闷,奖励-50;考试通过了,心情大好,奖励+100;考试没通过,回家挨训-100。(假设,考前复习一定通过,玩游戏一定不通过),那么:
- 考前游戏+10,考试没通过-100,最后得到-90的奖励。
- 考前复习-50,考试通过+100,最后得到+50的奖励。
如果我们单纯地只从当前的一个奖励
r
r
r 来衡量一个动作(“游戏”or“复习”)的好坏,那肯定是游戏得到的奖励
r
r
r 更多
我们要把未来的奖励也计算到当前状态下,再进行决策。
2.V值和Q值的理解
-
V V V值:评估状态的价值,我们称为 V V V值。它代表了智能体在这个状态下,一直到最终状态得到总的奖励的期望。
-
Q Q Q值:评估动作的价值,我们称为 Q Q Q值。它代表了智能体选择该动作后,一直到最终状态得到总的奖励的期望。
3.V值介绍
V V V值定义:评估状态的价值,我们称为 V V V值。它代表了智能体在这个状态下,一直到最终状态得到总的奖励的期望。
V V V值计算:就是要计算当前状态 S S S到最终状态,得到总的奖励的期望值。通俗来说就是:从某个状态,按照策略 π \pi π,走到最终状态时,最终获得奖励总和的平均值(奖励期望),就是 V V V值。
【举例】 以下图为例,从状态
s
0
s_0
s0开始可以执行两个动作,分别是
a
1
a_1
a1和
a
2
a_2
a2。从状态
s
0
s_0
s0开始,执行动作
a
1
a_1
a1,到最终状态得到的总奖励
R
1
R_1
R1为+10;从状态
s
0
s_0
s0开始,执行动作
a
2
a_2
a2,到最终状态得到的总奖励
R
2
R_2
R2为+20。

假设1: 在状态 s 0 s_0 s0时,执行动作 a 1 a_1 a1的概率为40%,执行动作 a 2 a_2 a2的概率为60%,那么从状态 s 0 s_0 s0到最后状态时,得到的奖励期望为:
V = R ‾ = p ( a 1 ∣ s 0 ) ⋅ R 1 + p ( a 2 ∣ s 0 ) ⋅ R 2 = 40 % ⋅ 10 + 60 % ⋅ 20 = 16 \begin{aligned} V = \overline{R} &= p(a_1|s_0) \cdot {R_1} + p(a_2|s_0) \cdot {R_2} \\ &= 40\% \cdot 10+60\% \cdot 20 \\ &=16\\ \end{aligned} V=R=p(a1∣s0)⋅R1+p(a2∣s0)⋅R2=40%⋅10+60%⋅20=16
其中, p ( a 1 ∣ s 0 ) p(a_1|s_0) p(a1∣s0)是指在状态 s 0 s_0 s0时,选择动作 a 1 a_1 a1的概率; p ( a 2 ∣ s 0 ) p(a_2|s_0) p(a2∣s0)是指在状态 s 0 s_0 s0时,选择动作 a 2 a_2 a2的概率。
假设2: 在状态 s 0 s_0 s0时,执行动作 a 1 a_1 a1的概率为50%,执行动作 a 2 a_2 a2的概率为50%。那么从状态 s 0 s_0 s0到最后状态得到的奖励期望 R ‾ \overline{R} R为:
V = R ‾ = p ( a 1 ∣ s 0 ) ⋅ R 1 + p ( a 2 ∣ s 0 ) ⋅ R 2 = 50 % ⋅ 10 + 50 % ⋅ 20 = 15 \begin{aligned} V = \overline{R} &= p(a_1|s_0) \cdot {R_1} + p(a_2|s_0) \cdot {R_2} \\ &= 50\% \cdot 10+50\% \cdot 20 \\ &=15\\ \end{aligned} V=R=p(a1∣s0)⋅R1+p(a2∣s0)⋅R2=50%⋅10+50%⋅20=15
假设3: 在状态 s 0 s_0 s0时,执行动作 a 1 a_1 a1的概率为60%,执行动作 a 2 a_2 a2的概率为40%。那么从状态 s 0 s_0 s0到最后状态得到的奖励期望 R ‾ \overline{R} R为:
V = R ‾ = p ( a 1 ∣ s 0 ) ⋅ R 1 + p ( a 2 ∣ s 0 ) ⋅ R 2 = 60 % ⋅ 10 + 40 % ⋅ 20 = 14 \begin{aligned} V = \overline{R} &= p(a_1|s_0) \cdot {R_1} + p(a_2|s_0) \cdot {R_2} \\ &= 60\% \cdot 10+40\% \cdot 20 \\ &=14\\ \end{aligned} V=R=p(a1∣s0)⋅R1+p(a2∣s0)⋅R2=60%⋅10+40%⋅20=14
由上述三个假设可以看到:采取不同的策略 π \pi π方案,最终得到的 V V V值是不同的!!!也就是说, V V V值跟策略 π \pi π具有直接关系。
4.Q值介绍
Q Q Q值定义:评估动作的价值,我们称为 Q Q Q值。它代表了智能体选择该动作后,一直到最终状态得到总的奖励的期望。
Q Q Q值计算:就是要计算采取动作 A A A之后,到最终状态时,得到总的奖励的期望值。通俗来说就是:从某个动作出发,走到最终状态时,最终获得奖励总和的平均值(奖励期望),就是 Q Q Q值。
注:与V值不同,Q值和策略 π \pi π并没有直接关系,而是与环境的状态转移概率有关(环境的状态转移概率是未知的,我们无法学习也无法改变)。
【举例】 以下图为例,采取动作
a
1
a_1
a1,跳转到状态
s
1
s_1
s1,到最终状态时,得到的奖励为+10;跳转到状态
s
2
s_2
s2,到最终状态时,得到的奖励为+20;跳转到状态
s
3
s_3
s3,到最终状态时,得到的奖励为+5;

Q ( s 0 ) = R ‾ ( s 0 ) = p ( s 1 ∣ s 0 , a 1 ) ⋅ R 1 + p ( s 2 ∣ s 0 , a 1 ) ⋅ R 2 + p ( s 3 ∣ s 0 , a 1 ) ⋅ R 3 = p ( s 1 ∣ s 0 , a 1 ) ⋅ 10 + p ( s 2 ∣ s 0 , a 1 ) ⋅ 20 + p ( s 3 ∣ s 0 , a 1 ) ⋅ 5 \begin{aligned} Q(s_0) = {\overline R}(s_0) &= p(s_1|s_0,a_1) \cdot {R_1} + p(s_2|s_0,a_1) \cdot {R_2} + p(s_3|s_0,a_1) \cdot {R_3} \\ &= p(s_1|s_0,a_1) \cdot {10} + p(s_2|s_0,a_1) \cdot {20} + p(s_3|s_0,a_1) \cdot {5} \\ \end{aligned} Q(s0)=R(s0)=p(s1∣s0,a1)⋅R1+p(s2∣s0,a1)⋅R2+p(s3∣s0,a1)⋅R3=p(s1∣s0,a1)⋅10+p(s2∣s0,a1)⋅20+p(s3∣s0,a1)⋅5
其中,
p
(
s
1
∣
s
0
,
a
1
)
p(s_1|s_0,a_1)
p(s1∣s0,a1)是指在状态
s
0
s_0
s0时,选择动作
a
1
a_1
a1后跳转到状态
s
1
s_1
s1的概率;
p
(
s
2
∣
s
0
,
a
1
)
p(s_2|s_0,a_1)
p(s2∣s0,a1)是指在状态
s
0
s_0
s0时,选择动作
a
1
a_1
a1后跳转到状态
s
2
s_2
s2的概率;
p
(
s
3
∣
s
0
,
a
1
)
p(s_3|s_0,a_1)
p(s3∣s0,a1)是指在状态
s
0
s_0
s0时,选择动作
a
1
a_1
a1后跳转到状态
s
3
s_3
s3的概率。
注意:状态转移概率 p ( s 1 ∣ s 0 , a 1 ) p(s_1|s_0,a_1) p(s1∣s0,a1)、 p ( s 2 ∣ s 0 , a 1 ) p(s_2|s_0,a_1) p(s2∣s0,a1)、 p ( s 3 ∣ s 0 , a 1 ) p(s_3|s_0,a_1) p(s3∣s0,a1) 是系统决定的,我们无法学习也无法改变。
5.根据Q值计算V值
V
V
V值代表了智能体在这个状态下,一直到最终状态得到总的奖励的期望。一个状态的
V
V
V值,就是这个状态下的所有动作的
Q
Q
Q值,在策略
π
\pi
π下的期望。

V π ( s 0 ) = p ( a 1 ∣ s 0 ) ⋅ q ( s 0 , a 1 ) + p ( a 2 ∣ s 0 ) ⋅ q ( s 0 , a 2 ) = ∑ a ∈ A π ( a ∣ s 0 ) ⋅ q π ( s 0 , a ) \begin{aligned} V_\pi(s_0)&= p(a_1|s_0) \cdot q(s_0,a_1) + p(a_2|s_0) \cdot q(s_0,a_2) \\ &= \sum\limits_{a\in A} \pi(a|s_0) \cdot q_{\pi}(s_0, a) \end{aligned} Vπ(s0)=p(a1∣s0)⋅q(s0,a1)+p(a2∣s0)⋅q(s0,a2)=a∈A∑π(a∣s0)⋅qπ(s0,a)
其中,
p
(
a
1
∣
s
0
)
p(a_1|s_0)
p(a1∣s0)是指在状态
s
0
s_0
s0下选择动作
a
1
a_1
a1的概率;
q
(
s
0
,
a
1
)
q(s_0,a_1)
q(s0,a1)是指在状态
s
0
s_0
s0下选择动作
a
1
a_1
a1后的
Q
Q
Q值(获得的奖励期望);
p
(
a
2
∣
s
0
)
p(a_2|s_0)
p(a2∣s0)是指在状态
s
0
s_0
s0下选择动作
a
2
a_2
a2的概率;
q
(
s
0
,
a
2
)
q(s_0,a_2)
q(s0,a2)是指在状态
s
0
s_0
s0下选择动作
a
2
a_2
a2后的
Q
Q
Q值(获得的奖励期望);
π
(
a
∣
s
0
)
\pi(a|s_0)
π(a∣s0)是指策略
π
\pi
π在状态
s
0
s_0
s0时采取某个动作
a
∈
A
,
A
=
(
a
1
,
a
2
,
a
3
,
…
,
a
n
)
a\in A,A=(a_1, a_2, a_3, …, a_n)
a∈A,A=(a1,a2,a3,…,an)的概率;
q
π
(
s
0
,
a
)
q_{\pi}(s_0, a)
qπ(s0,a)是指在状态
s
0
s_0
s0时,采取某个动作
a
∈
A
,
A
=
(
a
1
,
a
2
,
a
3
,
…
,
a
n
)
a\in A,A=(a_1, a_2, a_3, …, a_n)
a∈A,A=(a1,a2,a3,…,an)对应的
Q
Q
Q值(获得的奖励期望)。
6.根据V值计算Q值
定义
q
π
(
s
0
,
a
1
)
q_\pi(s_0, a_1)
qπ(s0,a1)为某个状态
s
0
s_0
s0时,根据策略
π
\pi
π采取动作
a
1
a_1
a1的
Q
Q
Q值。
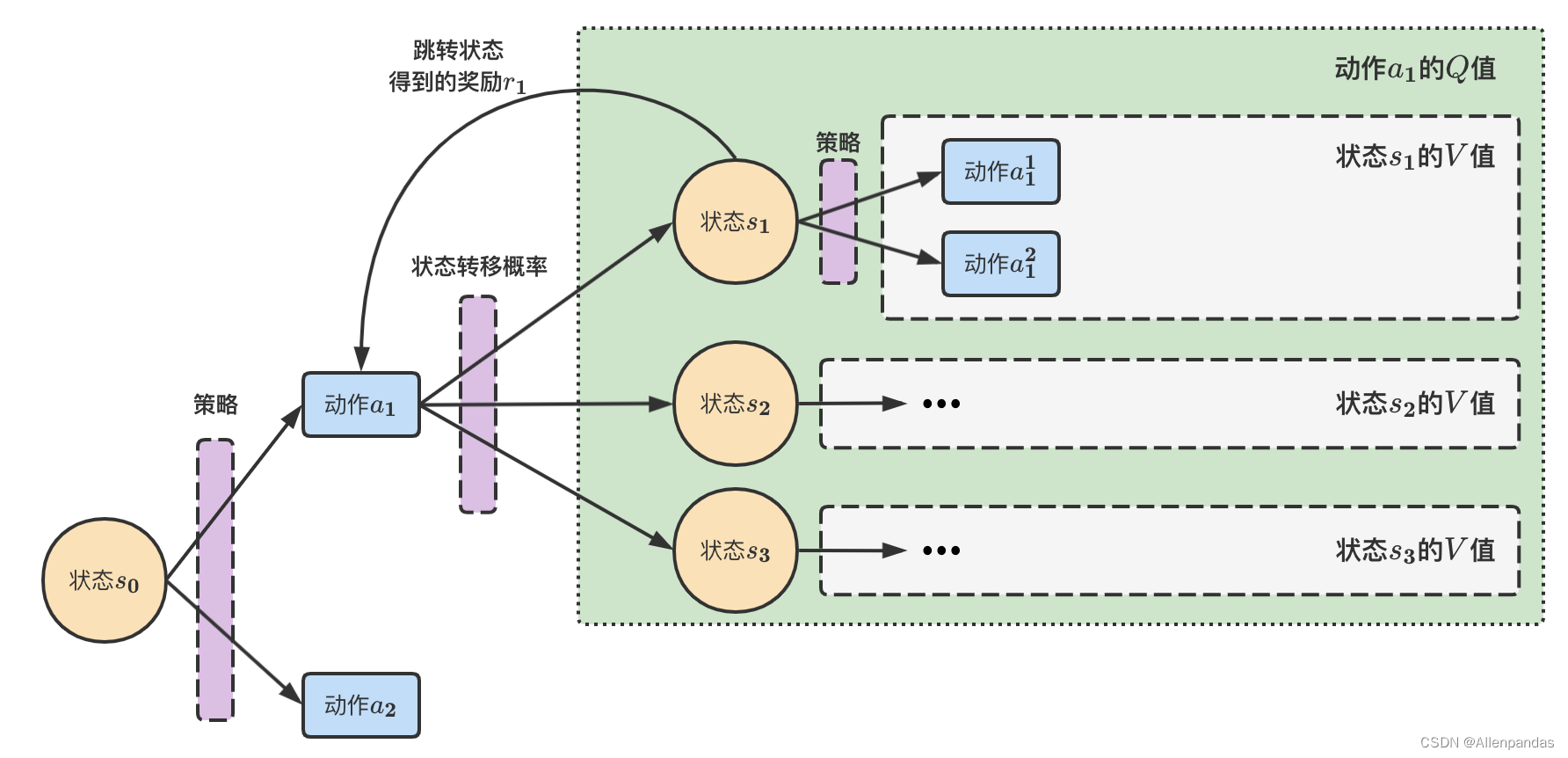
q π ( s 0 , a 1 ) = [ p ( s 1 ∣ s 0 , a 1 ) ⋅ v π ( s 1 ) + r 1 ] + [ p ( s 2 ∣ s 0 , a 1 ) ⋅ v π ( s 2 ) + r 2 ] + [ p ( s 3 ∣ s 0 , a 1 ) ⋅ v π ( s 3 ) + r 3 ] = [ r 1 + r 2 + r 3 ] + P ( s ′ ∣ s 0 , a 1 ) ⋅ v π ( s ′ ) = R s 0 a 1 + γ ∑ s ′ P s 0 s ′ a 1 ⋅ v π ( s ′ ) \begin{aligned} q_\pi(s_0, a_1) &= [p(s_1|s_0,a_1) \cdot v_\pi(s_1) + r_1] + [p(s_2|s_0,a_1) \cdot v_\pi(s_2) + r_2] + [p(s_3|s_0,a_1) \cdot v_\pi(s_3) + r_3]\\ &=[ r_1+r_2+r_3] + P(s'|s_0, a_1) \cdot v_{\pi}(s')\\ &=R_{s_0}^{a_1} + \gamma \sum\limits_{s'} P_{{s_0}s'}^{a_1} \cdot v_\pi(s')\\ \end{aligned} qπ(s0,a1)=[p(s1∣s0,a1)⋅vπ(s1)+r1]+[p(s2∣s0,a1)⋅vπ(s2)+r2]+[p(s3∣s0,a1)⋅vπ(s3)+r3]=[r1+r2+r3]+P(s′∣s0,a1)⋅vπ(s′)=Rs0a1+γs′∑Ps0s′a1⋅vπ(s′)
其中,
R
s
0
a
1
R_{s_0}^{a_1}
Rs0a1是指在状态
s
0
s_0
s0时,采取动作
a
1
a_1
a1跳转到新状态得到的奖励;
γ
\gamma
γ是折扣因子;
P
s
0
s
′
a
1
P_{{s_0}s'}^{a_1}
Ps0s′a1是指在状态
s
0
s_0
s0时,采取动作
a
1
a_1
a1,跳转到新状态
s
′
s'
s′的状态转移概率;
v
π
(
s
′
)
v_\pi(s')
vπ(s′)是指跳转到的新状态
s
′
s'
s′的
V
V
V值。
7.根据V值计算V值
更多的时候,我们需要根据 V V V值来计算 V V V值。准确的说,是根据后面状态 s ′ s' s′的 V V V值来计算前面状态 s s s的 V V V值。
已知:
V
π
(
s
0
)
=
p
(
a
1
∣
s
0
)
⋅
q
(
s
0
,
a
1
)
+
p
(
a
2
∣
s
0
)
⋅
q
(
s
0
,
a
2
)
=
∑
a
∈
A
π
(
a
∣
s
0
)
⋅
q
π
(
s
0
,
a
)
\begin{aligned} V_\pi(s_0)&= p(a_1|s_0) \cdot q(s_0,a_1) + p(a_2|s_0) \cdot q(s_0,a_2) \\ &= \sum\limits_{a\in A} \pi(a|s_0) \cdot q_{\pi}(s_0, a) \\ \end{aligned}
Vπ(s0)=p(a1∣s0)⋅q(s0,a1)+p(a2∣s0)⋅q(s0,a2)=a∈A∑π(a∣s0)⋅qπ(s0,a)
q π ( s 0 , a 1 ) = [ p ( s 1 ∣ s 0 , a 1 ) ⋅ v π ( s 1 ) + r 1 ] + [ p ( s 2 ∣ s 0 , a 1 ) ⋅ v π ( s 2 ) + r 2 ] + [ p ( s 3 ∣ s 0 , a 1 ) ⋅ v π ( s 3 ) + r 3 ] = [ r 1 + r 2 + r 3 ] + P ( s ′ ∣ s 0 , a 1 ) ⋅ v π ( s ′ ) = R s 0 a 1 + γ ∑ s ′ P s 0 s ′ a 1 ⋅ v π ( s ′ ) q π ( s 0 , a 2 ) = R s 0 a 2 + γ ∑ s ′ P s 0 s ′ a 2 ⋅ v π ( s ′ ) \begin{aligned} q_\pi(s_0, a_1) &= [p(s_1|s_0,a_1) \cdot v_\pi(s_1) + r_1] + [p(s_2|s_0,a_1) \cdot v_\pi(s_2) + r_2] + [p(s_3|s_0,a_1) \cdot v_\pi(s_3) + r_3]\\ &=[ r_1+r_2+r_3] + P(s'|s_0, a_1) \cdot v_{\pi}(s')\\ &=R_{s_0}^{a_1} + \gamma \sum\limits_{s'} P_{{s_0}s'}^{a_1} \cdot v_\pi(s')\\ q_\pi(s_0, a_2) &=R_{s_0}^{a_2} + \gamma \sum\limits_{s'} P_{{s_0}s'}^{a_2} \cdot v_\pi(s')\\ \end{aligned} qπ(s0,a1)qπ(s0,a2)=[p(s1∣s0,a1)⋅vπ(s1)+r1]+[p(s2∣s0,a1)⋅vπ(s2)+r2]+[p(s3∣s0,a1)⋅vπ(s3)+r3]=[r1+r2+r3]+P(s′∣s0,a1)⋅vπ(s′)=Rs0a1+γs′∑Ps0s′a1⋅vπ(s′)=Rs0a2+γs′∑Ps0s′a2⋅vπ(s′)
所以:
V
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
⋅
[
R
s
a
+
γ
∑
s
′
∈
S
P
s
s
′
a
⋅
v
π
(
s
′
)
]
\begin{aligned} V_\pi(s)&= \sum\limits_{a\in A} \pi(a|s) \cdot[ R_{s}^a + \gamma\sum\limits_{s'\in S} P_{ss'}^{a} \cdot v_\pi(s') ] \\ \end{aligned}
Vπ(s)=a∈A∑π(a∣s)⋅[Rsa+γs′∈S∑Pss′a⋅vπ(s′)]
参考文献:
[1] 张斯俊, 如何理解强化学习中的Q值和V值?


























 1040
1040

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










