低通 PCA DCT对图像噪声处理

低通 PCA DCT 对图像噪声的处理

近期在学习这三种滤波器，还在初级阶段，贴一些程序在这里。
我想完成的是利用这三种滤波器对图像进行去噪声处理，emmm…，效果大家自己看图~

1 理想低通

理想低通，一般最理想的二维低通滤波器长这个样子：

二维理想低通滤波器的表达式为：

其中D0为截止频率，D(u,v)的计算方式也就是两点间的距离，一般为：

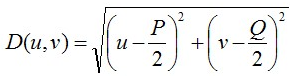
使用低通滤波器所得到的结果如下所示。低通滤波器允许低频成分通过，滤除高频成分，所以使得图像模糊。由于理想低通滤波器过于理想，变化没有缓冲，所以会产生振铃现象。

相关代码：

A = imread('Fig0413(a)(original_test_pattern).tif');
figure;
subplot(1,2,1) 
imshow(A); 
s=fftshift(fft2(A)); 
%生成ILPF并对白条图像进行低通滤波
[M,N]=size(s); 
H = zeros(M,N);
n1=floor(M/2); %对M/2进行取整
n2=floor(N/2); 
d0=40; 
for i=1:M   
    for j=1:N   
        d=sqrt((i-n1)^2+(j-n2)^2); %点(i,j)到Fourier变换中心的距离
        h = double(d<=d0); %ILPF滤波函数
        s(i,j)=h*s(i,j);           %ILPF滤波后的频域表示
         H(i,j) = h;                % ILPF滤波器
    end
end
%进行反Fourier变换并显示
s=ifftshift(s);   
s=uint8(real(ifft2(s)));%对s进行二维反离散的Fourier变换后，取复数的实部转化为无符号8位整数
subplot(1,2,2);
imshow(s);
figure;
subplot(1,2,1);
imshow(H);%二维显示ILPF
subplot(1,2,2);
mesh(H);%三维显示ILPF

2 PCA去噪

PCA（主成分分析）是一种掌握事物主要矛盾的统计分析方法，它可以从多元事物中解析出主要影响因素，揭示事物的本质，简化复杂的问题。计算主成分的目的是将高维数据投影到较低维空间。给定 n 个变量的m个观察值，形成一个n* m 的数据矩阵，n 通常比较大。对于一个由多个变量描述的复杂事物，人们难以认识，那么是否可以抓住事物主要方面进行重点分析呢？如果事物的主要方面刚好体现在几个主要变量上，我们只需要将这几个变量分离出来，进行详细分析。但是，在一般情况下，并不能直接找出这样的关键变量。这时我们可以用原有变量的线性组合来表示事物的主要方面， PCA 就是这样一种分析方法。
PCA 的目标是寻找r(r<n)个新变量，使它们反映事物的主要特征，压缩原有数据矩阵的规模。每个新变量是原有变量的线性组合，体现原有变量的综合效果，具有一定的实际含义。这 r 个新变量称为“主成分”，它们可以在很大程度上反映原来 n 个变量的影响，并且这些新变量是互不相关的，也是正交的。通过主成分分析，压缩数据空间，将多元数据的特征在低维空间里直观地表示出来。
PCA的算法过程如下：
1 将所获得的n个指标(每一指标有m个样品）的一批数据写成一个(mxn)维数据矩阵

2 对矩阵A作标准化处理：即对每一个指标分量进行标准化处理，从而得到$$X_{ij}=(x_{ij}{)}_{mxn}$$
3 计算样本矩阵的相关系数矩阵 :

4 运用Jacobi迭代方法计算R的特征值$${\lambda }_1,...,{\lambda }_n$$
即对应的特征向量$$v_1,...,v_n$$
5 特征值按降序排序(通过选择排序)得$${\lambda }_1^{\prime },...,{\lambda }_n^{\prime }$$并对特征向量进行相应调整得$$v_1^{\prime },...,v_{}$$