Markdown语法之数学公式【总结】（二）

上一篇文章：Markdown语法之数学公式【总结】

---

---

如果你已经有了一点 markdown 数学公式语法基础了，那么本文帮助你进阶，让你写出更加优美且复杂但实用的数学公式出来。

---

---

首先确定一点，如果你使用的是typera，确保勾选使用数学公式。 File 栏下的 Preferences偏好设置，

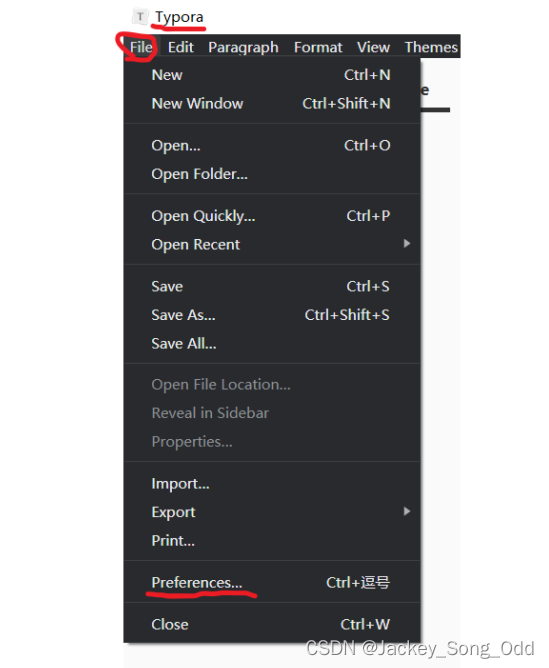
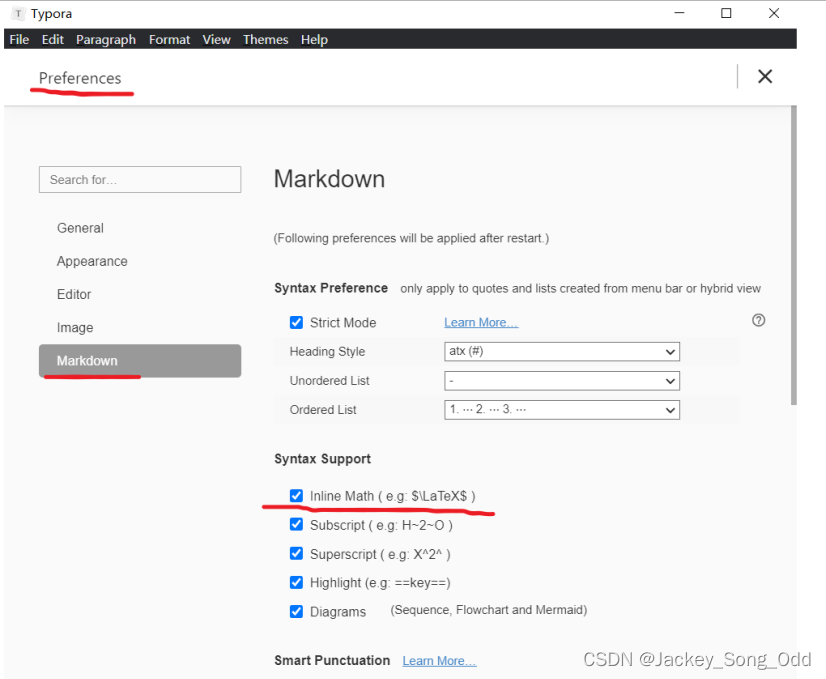
Markdown 一栏下，勾选 Inline Math。

markdown语法中，数学公式使用两个美元符号包裹。
例如：$P(\overline{A})=1-P(A)$，渲染结果为 $P(\overline{A})=1-P(A)$

符号的下位和上位

下位

对要加入下位的符号后面加入\limits_{下位内容}

以求极限为例，在 “$\lim$” 下位加入 “$x\to +\infty$”，$\lim\limits_{x\rightarrow+\infty}$，渲染效果 $\underset{x\to +\infty }{\lim }$

以求和符号为例，在 “$\sum$” 下位加入 “$i=0$”，$\sum\limits_{i=0}$，渲染效果 $\sum _{i=0}$

以求交并集为例，交：$\bigcap\limits_{i=0}$，并：$\bigcap\limits_{i=0}$，渲染效果 交：$\bigcap _{i=0}$，并：$\bigcap _{i=0}$

上位

\stackrel{上位内容}{上位符号}
以求和符号为例：在求和符号 $\sum$ 上加入 $n$，$\stackrel{n}{\sum}$，渲染效果 $\sum ^n$

求和符号上下位放在一起就有了 $\stackrel{n}{\sum\limits_{i=0}}$，渲染效果 $\stackrel{n}{\sum _{i=0}}$

例如 “数列的前 $n$ 项和” 表示为 $S_n=\stackrel{n}{\sum\limits_{i=1}}a_i=a_1+a_2+\cdots+a_n$，
渲染效果 $S_n=\stackrel{n}{\sum _{i=1}}{a}_i=a_1+a_2+\cdots +a_n$

再例如：$\overline{\stackrel{\infty}{\bigcup\limits_{i=1}}A_i}=\stackrel{\infty}{\bigcap\limits_{i=1}}\overline{A_i},\quad \overline{\stackrel{\infty}{\bigcap\limits_{i=1}}A_i}=\stackrel{\infty}{\bigcup\limits_{i=1}}\overline{A_i}.$，其中 \infty表示 $\infty$ 无穷大，\overline{上划线内容} 为加入上划线，
渲染效果 $\overline{\stackrel{\infty }{\bigcup _{i=1}}{A}_i}=\stackrel{\infty }{\bigcap _{i=1}}\overline{A_i},\overline{\stackrel{\infty }{\bigcap _{i=1}}{A}_i}=\stackrel{\infty }{\bigcup _{i=1}}\overline{A_i}.$

随机变量分布律

“~” 服从符号需要转义 \sim
比如正态分布：$X\sim N(0,{\sigma }^2)$. 它的写法为：$X\sim N(0,\sigma^2)$，其中 \sigma 为希腊字母 $\sigma$.

复合函数或多个式子组合

例如：$F_Y(y)=\{\begin{array}{ll}0,& y<0,\\ y^{\frac{3}{2}},& 0\le y<1,\\ 1,& y\ge 1.\end{array}$
它的写法为 $F_Y(y)=\begin{cases}0,&y<0,\\y^{\frac{3}{2}},&0\leq y<1,\\1,&y\geq1.\end{cases}$
前面的 “ $F_Y(y)=$ ” 为正常写法 $F_Y(y)=$，后面的内容用 \begin{cases} 和 \end{cases}包裹，中间是内容，&后的内容为附加条件，\\为换行。

多个式子用花括号组合在一起，就可以用 \begin{cases} 和 \end{cases}包裹：
$\begin{cases}3x+y=1\\x^2+y^2=9\\x+2y=0\end{cases}$
渲染效果为：
$\{\begin{array}{l}3x+y=1\\ x^2+y^2=9\\ x+2y=0\end{array}$

导数、积分

$f(x)$ 的导数写为 $f^{\prime }(x)$ $f^{\prime}(x)$，f ^上角标内容为\prime 一小撇 “ $\prime$ ”。

$$\int_{-\infty}^{+\infty}f(x)$$，其中 \int 是积分符号，渲染效果如下：$${\int }_{-\infty }^{+\infty }f(x)$$

$$
P(X<1,X+Y<4)=\int_0^1\mathrm{d}x\int_2^{4-x}\dfrac{1}{8}(6-x-y)\mathrm{d}y
$$
渲染效果如下：
$$P(X<1,X+Y<4)={\int }_0^1\mathrm{d}x{\int }_2^{4-x}\frac{1}{8}(6-x-y)\mathrm{d}y$$
注意大公式用两个美元符号 “$$” 分行包裹，渲然效果更好。

---

---

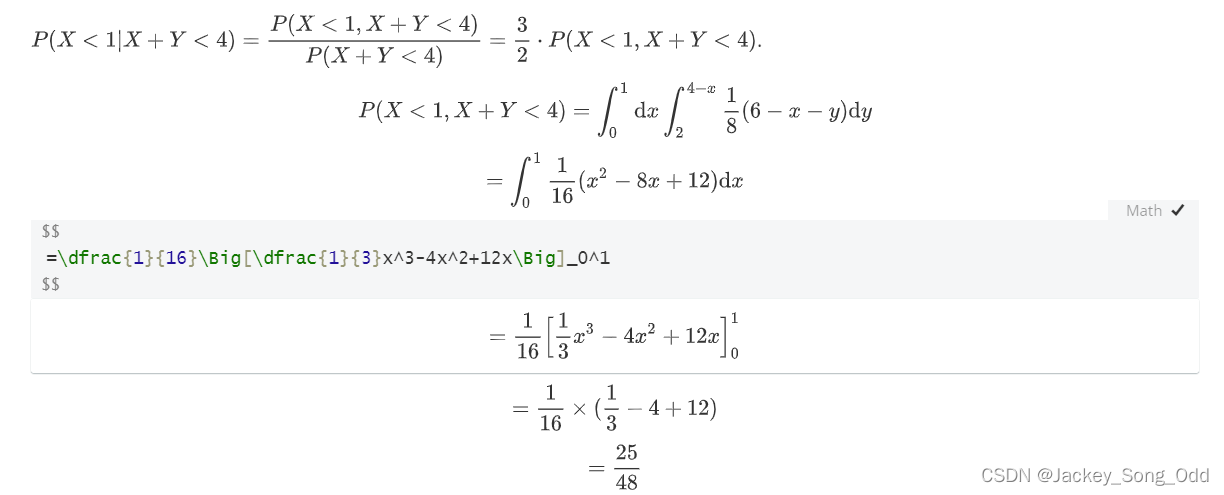
应用：
设连续型随机变量 $X$ 的分布函数为 $F(x)=\{\begin{array}{ll}A+B{e}^{-2x},& x>0,\\ 0,& x\le 0.\end{array}$.
$F(x)=\begin{cases}A+Be^{-2x},&x>0,\\0,&x\leq0.\end{cases}$

• 确定 $A,B$ 的值；
• 求 $P(-1<x<1)$;.
• 求概率密度函数 $f_X(x)$;
• 若 $Y=3X+1$，求概率密度函数 $f_Y(y)$.

解：(1)

$\because 0\le F(x)\le 1$

$\therefore 1=\lim x\to +\infty F(x)=\underset{x\to +\infty }{\lim }(A+B{e}^{-2x})=A$.
$\therefore 1=\lim\limits{x\rightarrow+\infty}F(x)=\lim\limits_{x\rightarrow+\infty}(A+Be^{-2x})=A$.

$\therefore A=1$.

又 $\because$ 分布函数 $F(x)$ 右连续，

$\therefore 0=F(0)=\underset{x\to 0^{+}}{\lim }F(x)=\underset{x\to 0^{+}}{\lim }(A+B{e}^{-2x})=A+B=1+B$.
$\therefore 0=F(0)=\lim\limits_{x\rightarrow0^+}F(x)=\lim\limits_{x\rightarrow0^+}(A+Be^{-2x})=A+B=1+B$.

$\therefore B=-1$.

$\therefore F(x)=\{\begin{array}{ll}1-e^{-2x},& x>0,\\ 0,& x\le 0.\end{array}$.
$\therefore F(x)=\begin{cases}1-e^{-2x},&x>0,\\0,&x\leq0.\end{cases}$.

(2) $P(-1<x<1)=F(1)-F(0)=(1-e^{-2})-0=1-\frac{1}{e^2}$.

(3) $f_X(x)=F_X^{\prime }(x)$. $f_X(x)=F_X^\prime(x)$.

$f(x)=F^{\prime }(x)=\{\begin{array}{ll}0,& x\le 0,\\ 2e^{-2x},& x>0.\end{array}$.
$f(x)=F^\prime(x)=\begin{cases}0,&x\leq0,\\2e^{-2x},&x>0.\end{cases}$.

(4) $\because Y=3X+1$，又 $\because x>0$，

$\therefore y>1$.

$F_Y(y)=P(Y\le y)=P(3X+1\le y)=\{\begin{array}{ll}0,& y\le 1,\\ P(X\le \frac{y-1}{3}),& y>1.\end{array}$.
$F_Y(y)=P(Y\leq y)=P(3X+1\leq y)=\begin{cases}0,&y\leq1,\\P(X\leq\dfrac{y-1}{3}),&y>1.\end{cases}$

计算得到，当 $y>1$ 时：
$$F_Y(y)=P(\frac{y-1}{3}\le X)=F_X\left(\frac{y-1}{3}\right)=1-e^{-\frac{2}{3}(y-1)}$$
$F_Y(y)=P(\dfrac{y-1}{3}\leq X)=F_X\Big(\dfrac{y-1}{3}\Big)=1-e^{-\frac{2}{3}(y-1)}$

$\therefore F_Y(y)=P(Y\le y)=P(3X+1\le y)=\{\begin{array}{ll}0,& y\le 1,\\ 1-e^{-\frac{2}{3}(y-1)},& y>1.\end{array}$.
$\therefore F_Y(y)=P(Y\leq y)=P(3X+1\leq y)=\begin{cases}0,&y\leq1,\\1-e^{-\frac{2}{3}(y-1)},&y>1.\end{cases}$

$\therefore f_Y(y)=F_Y^{\prime }(y)=\{\begin{array}{ll}0,& y\le 1,\\ \frac{2}{3}{e}^{-\frac{2}{3}(y-1)},& y>1.\end{array}$.
$\therefore f_Y(y)=F^\prime_Y(y)=\begin{cases}0,&y\leq1,\\\dfrac{2}{3}e^{-\frac{2}{3}(y-1)},&y>1.\end{cases}$

---

应用：
$y=\sin x+\cos x$ $y=\sin x + \cos x$：(非奇非偶函数，周期 $2\pi$ $2\pi$.)

$y=\sin x+\cos x=\sqrt{2}(\sin x\cdot \frac{\sqrt{2}}{2}+\cos x\cdot \frac{\sqrt{2}}{2})$
$y=\sin x+\cos x=\sqrt{2}(\sin x\cdot\dfrac{\sqrt{2}}{2}+\cos x\cdot\dfrac{\sqrt{2}}{2})$

$=\sqrt{2}(\sin x\cdot \cos \frac{\pi }{4}+\cos x\cdot \sin \frac{\pi }{4})$
$=\sqrt{2}(\sin x\cdot\cos\dfrac{\pi}{4}+\cos x\cdot\sin\dfrac{\pi}{4})$

$=\sqrt{2}\sin (x+\frac{\pi }{4})$.
$=\sqrt{2}\sin(x+\dfrac{\pi}{4})$

$y=\sqrt{2}\sin (x+\frac{\pi }{4})$ 由 $y=\sin x$ 左移了 $\frac{\pi }{4}$ 单位再整体乘以 $\sqrt{2}$ 得来。

---

洛必达与泰勒之争:

已知当 $x\to 0$ 时，$f(x)=3\sin x-\sin 3x$ 与 $c{x}^k$ 是等价无穷小，则（）.

$A.k=1,c=4B.k=1,c=-4C.k=3,c=4D.k=3,c=-4$.

解：由题意，有
$$\underset{x\to 0}{\lim }\frac{3\sin x-\sin 3x}{c{x}^k}=1,$$

$$
\lim\limits_{x\rightarrow0}\dfrac{3\sin x-\sin3x}{cx^k}=1,
$$

则
$$原式\stackrel{洛必达法则}{=}\underset{x\to 0}{\lim }\frac{3\cos x-3\cos 3x}{ck{x}^{k-1}}\stackrel{洛必达法则}{=}\underset{x\to 0}{\lim }\frac{-3\sin x+9\sin 3x}{ck(k-1)x^{k-2}}\stackrel{洛必达法则}{=}\underset{x\to 0}{\lim }\frac{-3\cos x+27\cos 3x}{ck(k-1)(k-2)x^{k-3}}$$

$$
原式\stackrel{洛必达法则}{=}\lim\limits_{x\rightarrow0}\dfrac{3\cos x-3\cos3x}{ckx^{k-1}}\stackrel{洛必达法则}{=}\lim\limits_{x\rightarrow0}\dfrac{-3\sin x+9\sin3x}{ck(k-1)x^{k-2}}\stackrel{洛必达法则}{=}\lim\limits_{x\rightarrow0}\dfrac{-3\cos x+27\cos3x}{ck(k-1)(k-2)x^{k-3}}
$$

$$=\underset{x\to 0}{\lim }\frac{24}{ck(k-1)(k-2)x^{k-3}}=1,$$

$$
=\lim\limits_{x\rightarrow0}\dfrac{24}{ck(k-1)(k-2)x^{k-3}}=1,
$$

于是 $k=3,c=4$

用了三次洛必达法则。