贪心算法——喷水装置

前言：作为算法小白又遇到难题了@_@，这篇文章的思路肯定不是很好，时间空间复杂度更是没法考虑，但是如果在拼题网遇到这题还是可以通过的，赞就不奢求了，心如死灰 (ノ— _ —)ノ。

问题描述

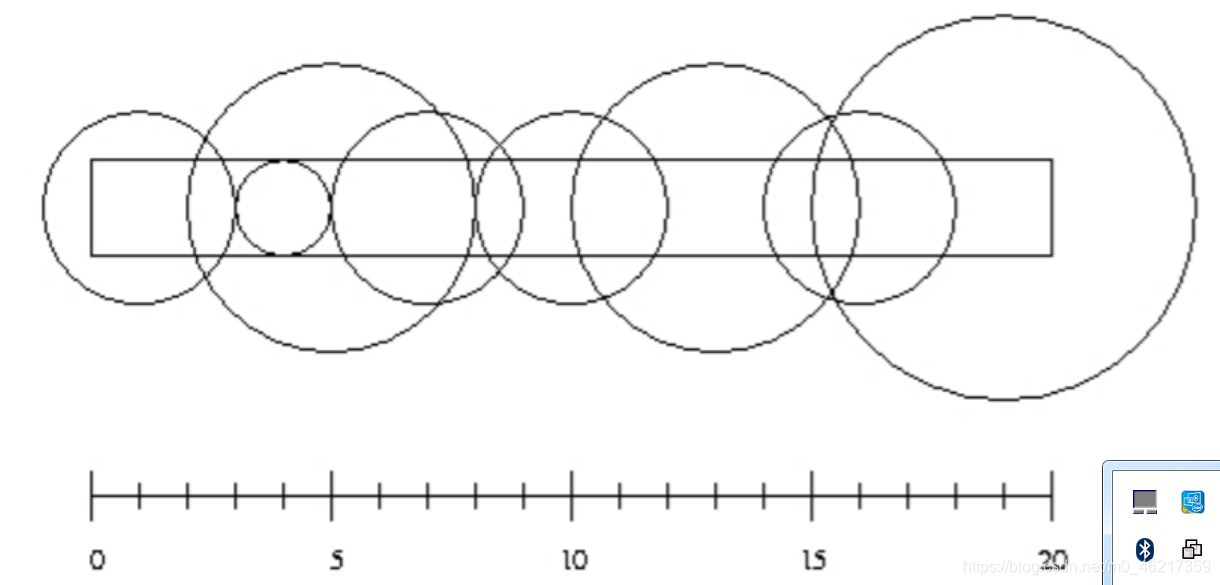
长L米，宽W米的草坪里装有n个浇灌喷头。每个喷头都装在草坪中心线上（离两边各W/2米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。

请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

输入格式

输入包含若干组测试数据。

第一行一个整数T表示数据组数。

每组数据的第一行是整数n、L和W的值，其中n≤10 000。

接下来的n行，每行包含两个整数，给出一个喷头的位置和浇灌半径。

如图1所示的示意图是样例输入的第一组数据所描述的情况。

输出格式

对每组测试数据输出一个数字，表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开还不能浇灌整块草坪，则输出-1。

输入样例

3
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1

输出样例

6
2
-1

思路解析

（1） 和看电影的题非常类似，不过是由线变了面，所以先看看图能发现什么

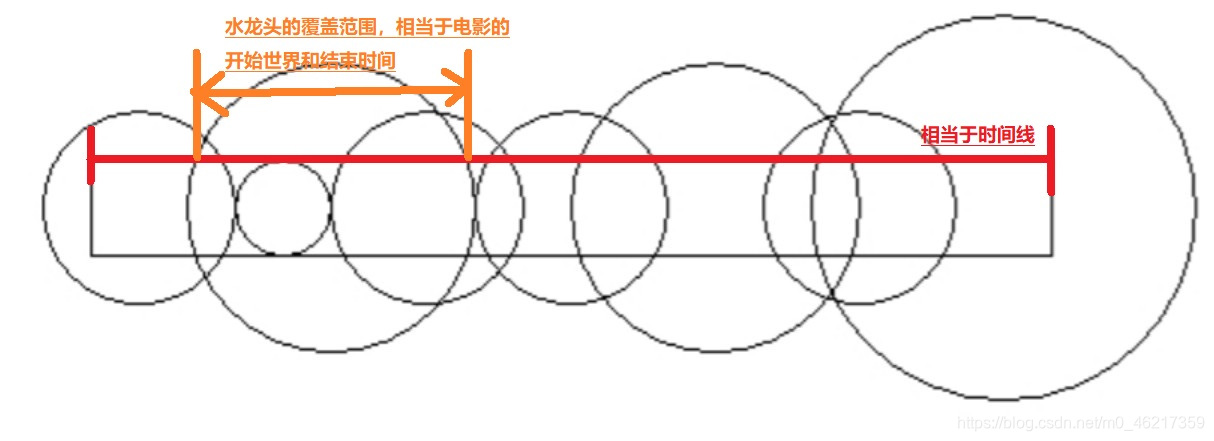
（2）看来得想办法根据半径(radius)和坐标(position)获得他覆盖的长度（cover_length)

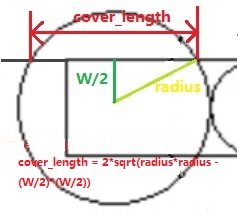
（3）假设一个极端情况，如果一个水龙头覆盖范围特别大，其他水龙头就很可能没啥用，所以要是能按照覆盖范围排个序该多好

（4）另一种极端情况，半径基本差不多，比如先选择灰色的O，要是我再按照覆盖范围去选就完蛋了，所以得选黄色的O

代码思路

（1）先用 sort 给所有水龙头按照覆盖范围弄个降序

bool cmp(tap tapA,tap tapB){
	return tapA.cover_length > tapB.cover_length;
}
//主函数内
sort(taps,taps + n,cmp);

（2）找到一个最合适的水龙头（并且它没用过，代码里用 isUse 表示）

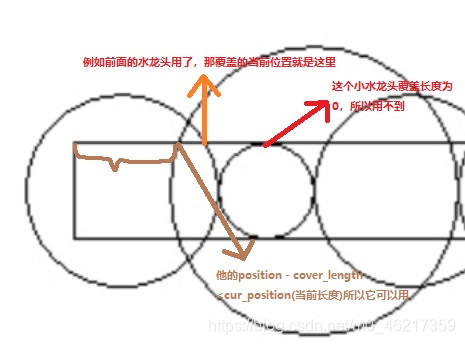
for(int i=0;i<n;i++){
			//找到没用过且左覆盖范围在当前位置之前或相等的，记录下来 
			if(taps[i].position - taps[i].cover_length / 2 <= cur_position && taps[i].isUse == false){	
				//如果坐标距离更远就记录下来 
				if(taps[i].position > rec_pos){
					rec_i = i;
					rec_pos = taps[i].position;
				}
			}	
		}

（3）用一个变量 cur_position 去记录当前已经覆盖的位置

cur_position = taps[rec_i].position + taps[rec_i].cover_length /