第一节 现值法
一、现值法的定义
根据资金等值的概念,将方案或项目在整个分析期内不同时点上发生的有关净现金流量,按照某一预定的收益率折算为起点(一般是项目的建设期起点)的现值,并以其累计值的大小作为衡量方案经济效益的依据,这种分析方法就是现值法。
如果计算方案的现值考虑了方案的投资、年收益、年支出、残值等分析期中的全部现金流量,那么所得到的现值称为净现值,一般用符号NPV表示。如果计算方案的现值时仅考虑了方案分析期中的支出与残值这两部分现金流量,这时的现值可视为是方案分析期中全部支出的现值,故称之为费用现值,一般用符号PC表示。
二、净现值法
1.净现值NPV定义及定义式。 所谓净现值是指按一定的折现率将方案计算期内各时点的净现金流量折现到计算期初的现值累加之和。
净现值的表达式为:![]() 或
或 
式中:
NPV——净现值
CIt ——第t年的现金流入额
COt ——第t年的现金流出额
n ——项目寿命年限(或计算期)
i0 ——基准折现率
Kt ——第t年的投资支出
CO ' t——第t年除投资支出以外的现金流出,即: COt = Kt + CO' t
2.净现值NPV的经济涵义
例:某方案的现金流如图,请计算出,该投资的收益率是多少?(i=12%)
如果, i0=12%,n=10年,P=100万,F=310.58万
NPV=0
若净现值等于零NPV=0,则表明:
①从投资回收期角度看,按照给定的贴现率,方案在寿命期内刚好收回投资;
②从定义式的含义看:项目各年的净现金流量的现值累计之和刚好为零;
③收益率i刚好等于项目的基准收益率(基准贴现率i0 ),即技术方案(项目)的获利能力等于给定的贴现率i0 ,即达到资本的最低获利要求。
若净现值大于零NPV>0,表明:
项目的获利能力高于贴现率,即高于资本的最低获利要求;有附加收益。
净现值小于零NPV<0,表明:
项目获利能力低于贴现率,即低于资本的最低获利要求。
由此可见:净现值指标的实质:是看方案的现金流的收益水平是否能够达到基准收益率的要求,即NPV是否大于零。
3.判别准则
对单一项目方案:若NPV≥0,则项目应予接受;若NPV<0,则项目应予拒绝。
多方案比选: 若方案间的投资规模相差不大时,净现值越大的方案相对越优(净现值最大准则)。
4.计算方法:①公式法 ②表格法
例:某项目的各年现金流量如下图所示,试用净现值指标判断项目的经济性?
i0=10%
公式法
表格法
静态投资回收期为4.88年;动态投资回收期为5.84年
累计净现金流量曲线
累计净现值曲线
5.净现值函数![]()
NCFt:净现金流量
NCFt 和 n 受到市场和技术进步的影响。在NCFt 和 n 确定的情况下,有![]()
例:
NPV(i)=-1000+400*[(1+i)^4-1]/[i*(1+i)^4]
当净现金流量和项目寿命期一定时,有

净现值函数的特点
若 i 连续变化,可得到右图所示的净现值函数曲线。同一净现金流量:i0 ↑,NPV ↓,甚至减小到零或负值,意味着可接受方案减少。 必然存在 i 的某一数值 i* ,使 NPV( i* ) = 0。

净现值对折现率的敏感性问题


可以看出,不同的基准折现率会使方案的评价结论截然不同,这是由于方案的净现值对折现率的敏感性不同。这一现象对投资决策具有重要意义。
NPV对i的敏感性在投资决策中的作用
有5个净现值大于0的项目A、B、C、D、E,总投资限额为K ,可以支持其中的4个项目:
1)对于i01,它们的优劣排序为:A、D、B、E、C
则选投项目A、D、B、E
2)当i01→i02(常因K的变化),其优劣排序为:A、E、C、D、B
则选投项目A、E、C、D
6.净现值NPV的优缺点
优点:
(1)计算较简便,考虑了资金的时间价值;考虑了项目整个寿命期内的现金流入流出情况。全面、科学。
(2)是一个绝对指标,反映了投资项目对企业财富的绝对贡献,与企业追求利润最大化的目标是一致的。所以在多方案的比选中,净现值最大化准则是合理的。
缺陷:
(1)需要预先给定折现率,这给项目决策带来了困难。因为若折现率定得略高,可行项目就可能被否定; 反之,折现率定得过低,不合理的项目就可能被选中。由此可见,净现值法的运用,折现率i0对方案的取舍影响很大,必须对折现率i0有较为客观的令人满意的估计。
(2) 净现值指标用于多方案比较时,没有考虑各方案投资额的大小,因而不能直接反映资金的利用效率,当方案间的初始投资额相差较大时,可能出现失误。为了考察资金的利用效率,人们通常用净现值指数(NPVI)作为净现值的辅助指标。
(3)对于寿命期不同的技术方案,不宜直接使用净现值(NPV)指标评价。
三、净现值率(NPVR / NPVI)
由于投资额往往是有限的,如果投资者很重视项目的投资效果,就要依据每单位投资的盈利性来衡量投资方案。
净现值率(净现值指数)(the net present value rate (index ),简写:NPVR/NPVI),又称净现值指数或净现值比,是按设定折现率求得的方案计算期的净现值与其全部投资现值的比率。一般情况下,净现值指数定义的表达式为:

式中:
NPVI ——净现值指数
NPV ——净现值指数
P——技术方案投资现值之和
说明: 净现值指数的经济含义,它是表示单位投资现值所取得的净现值额,也就是单位投资现值所获取的超额净效益。以净现值指数的最大化为决策目标,将有利于实现有限投资取得净贡献的最大化。
净现值指数NPVR判别准则:
独立方案或单一方案,NPVR≥0时方案可行。 多方案比选时,max{NPVRj≥0}的方案最好。
投资没有限制,进行方案比较时,原则上以净现值为判别依据。当投资有限制时,更要追求单位投资效率,辅以净现值率指标。净现值率常用于多方案的优劣排序。
例:某工程有A、B两种方案可行,现金流量如下表,设基准折现率为10%,试用净现值法和净现值率法择优。
四、 差额净现值∆NPV
设A、B为两个投资额不等的互斥方案,A方案的投资较大,则两方案的差额净现值可由下式求出:

式中:
∆NPV——差额净现值
(CIA—COA)t——方案A第t年的净现金流
(CIB—COB)t——方案B第t年的净现金流
NPVA,NPVB——分别为方案A与方案B的净现值
用增量分析法进行互斥方案比选时,若∆NPV ≥0。表明增量投资不仅达标而 且还有超额收益,是可以接受的,所以投资(现值)大的方案经济效果较好;若∆NPV <0,表明增量投资不可接受,投资(现值)小的方案经济效果较好。
有三个互斥方案A、B、C,其各年的现金流量如下表,若基准收益率为15%,请选择优方案。
第一步:先把方案按照初始投资的递升次序排列。设置零方案,零方案为全不投资方案。有时,可能所有互斥方案均不符合基本条件(不能通过绝对检验),此时的最佳方案是不投资。因此我们把全不投资也作为一个方案(即O方案)参与比选。
第二步:选择初始投资最少的方案作为临时最优方案,这里选定全不投资方案O,作为临时最优方案。
第三步:选择初始投资较高的方案A作为竞争方案。计算这两个方案的现金流量之差,并计算其差额净现值∆NPV A-O。假定i0=15%。则有:
如果差额净现值∆NPVA-O大于或等于零,则说明竞争方案A优于临时最优方案O;若差额净现值∆NPVA-O小于零,则临时最优方案不变。现在2026.32元大于零,所以应把临时最优方案O(即全不投资方案)淘汰而将A作为临时最优方案。
第四步:把上述步骤反复下去,直到所有方案都比较完毕,可以找到最后的最优方案。 现在以B作为竞赛方案,计算B和A两个方案现金流量之差的净现值∆NPVB-A:
∆NPVB-A为负,说明B方案较劣,把B方案淘汰,仍然保持A为临时最优方案。其次以C作为竞争方案,计算∆NPVC-A:
∆NPVC-A是大于零的,说明方案C优于A,方案C是最后的最优方案。
容易验证,按方案的净现值的大小直接进行比较,会和上述的投资增额净现值的比较有完全一致的结论。经计算可得各个互斥方案的净现值NPVA=2026.32元,NPVB=1535.72元,NPVC=2547.0元,按各方案净现值比较,C方案最优,与上述投资增额净现值法所得的结论一致。
五、费用现值
所谓费用现值是指按一定的折现率将方案计算期内各时点的现金流出折现到计算期初的现值累加之和。
在对多个方案比较选优时,如果诸方案产出价值相同,或者诸方案能够满足同样需要但其产出效益难以用价值形态(货币)计量(如环保、教育、保健、国防类项目)时,可以通过对各方案费用现值PC比较进行选择。
费用现值计算和判别
费用现值PC的定义式为:

式中:
PC——费用现值
说明:
①费用现值方法,是建立在假设基础上的。
②费用现值指标只能用于多个方案的比选,不能用于单个方案评价;
③其判别准则是:费用现值最小的方案为优;
例:某项目有三个采暖方案A、B、C,均能满足同样的取暖需要。其费用数据如下表所示。在基准折现率i0=10%的情况下,试用费用现值确定最优方案。
各方案的费用现值计算如下:
PCA=200+60(P/A,10%,10)=568.64(万元)
PCB=240+50(P/A,10%,10)=547.20(万元)
PCC=300+35(P/A,10%,10)=515.04(万元)
第二节 年值法
一、年值法的定义
根据资金等值的概念,将方案在整个分析期中不同时间点上发生的有关现金流量按照某一预定的收益率折算为整个分析期中每个时点上的等额现金流量序列(即年均值)并以此作为衡量方案或项目经济效益大小的依据,这种分析方法就叫年值法。
二、净年值(NAV)法
净年值(the net annual value,简写:NAV),或称平均年盈利(the average annual benefit ,简写AAB)指标。
其定义为:方案寿命期内的净现值用复利方法平均分摊到各个年度而得到的等额年盈利额。其表达式为:
![]()
说明:
① 经济含义:项目在寿命期内,附加收益的年金额。
② 判据:NAV≥0;
③考虑到方案间投资额的大小不同,也可采用净年值指数(NAVI)指标,
④净年值指数(NAVI)指标可以同时克服NAV有利于投资额大和寿命期长的方案的两个偏差,
⑤但是它的经济效益表达很不直观,常常使项目投资者或是经营者感到困惑,因此指标缺乏说服力,一般不用于单个方案的评价。即使多个方案的比较评价时,也只是作为辅助指标来考虑。
三、费用年值(AC)法
费用年值AC的定义式为:

式中:
AC——费用年值
说明:
①费用年值方法,是建立在假设基础上的。假定:参与评价的各个方案是可行的;适用于方案的产出价值相同,或者诸方案能够满足同样需要但其产出效益难以用价值形态(货币)计量;
②费用年值指标只能用于多个方案的比选,不能用于单个方案评价;
③其判别准则是:费用年值最小的方案为优;
例:某项目有三个采暖方案A、B、C,均能满足同样的取暖需要。其费用数据如下表所示。在基准折现率i0=10%的情况下,试用费用年值确定最优方案。
各方案的费用年值计算如下:
ACA=200(A/P,10%,10)+60=92.55(万元)
ACB=240(A/P,10%,10)+50=89.06(万元)
ACC=300(4/P,10%,10)+35=83.82(万元)
根据费用最小的选优准则,费用现值和费用年值的计算结果都表明,方案C最优,B次之,A最差。
费用现值与费用年值的关系,恰如前述净现值和净年值的关系一样,所以就评价结论而言,二者是等效评价指标。
第三节 内部收益率法
一、内部收益率的定义
定义:内部收益率IRR(Internal Rate of Return)是指使项目或方案在整个计算期内各年净现金流量的现值累计等于零(或净年值等于零)时的折现率。
其表达式为:

式中:
IRR——内部收益率,或内部报酬率
内部收益率的计算,除通过公式求得外,还可根据现金流量表中的累积净现值,用线性内插法计算求得。从经济意义上讲,内部收益率IRR的取值范围应是:-1<IRR<∞,大多数情况下的取值范围是0<IRR<∞。
二、内部收益率法的判别准则
计算求得的内部收益率IRR后,要与项目的设定收益率i0(财务评价时的行业基准收益率、国民经济评价时的社会折现率)相比较:
当IRR≥i0时,则表明项目的收益率已达到或超过设定折现率水平,项目可行,可以考虑接受;当IRR<i0时,则表明项目的收益率末达到设定折现率水平,项目不可行,应予拒绝。
基准收益率i0和基准投资回收期T0
不同地区、行业、时期, i0都有所区别。如表(基准投资收益率、基准投资回收期)
三、内部收益率的计算方法
由净现值函数曲线可知,随着折现率i0的不断增大,净现值NPV不断减小,当折现率增至i*时,项目净现值为零。此时i* 就是内部收益率IRR 。IRR可通过定义式解方程求得,但该式是一个高次方程,不容易直接求解。
通常采用"试算内插法"求IRR的近似解。求解过程如下:
先给出一个折现率i1,计算相应的NPV(i1),若NPV(i1)>0,说明IRR>i1, i1取小了。若NPV(i1)<0,说明IRR<i1, i1取大了。
据此,将折现率i1修正为i2,再求NPV(i2)的值。
如此反复试算,逐步逼近,最终可得到比较接近的两个折现率im与in,且im<in,使得NPV(im)>0,NPV(in)<0,然后用线性插值的方法确定IRR的近似值。公式见下。



例:某项目净现金流量如下表所示。当基准折现率i0=10%时,试用内部收益率指标判断该项目在经济效果上是否可以接受。
第一步:绘制现金流量图
第二步:用内插法求算IRR,列出方程:
第一次试算,依经验先取一个收益率,取il=12%,代入方程,求得:NPV(i1)=21(万元)>0 。由净现值函数曲线的特性知,收益率的取值偏小,应再取大些。
第二次试算,取i2=14%,代入方程求得:NPV(i2)=-91(万元)<0。可见,内部收益率必然在12%~14%之间,代入内插法计算式
可求得:IRR=12%+21/(21+91)×(14%-12%)=12.4%
第三步:分析判断方案可行性 因为,IRR=12.4%>i0=10%,所以,该方案是可行的。
四、内部收益率的经济涵义
内部收益率的经济涵义是,在项目的整个寿命期内,如果按利率i=IRR计算各年的净现金流量时,会始终存在着未能收回的投资,只有到了寿命期末时投资才能被全部收回,此时的净现金流量刚好等于零。
一般地讲,内部收益率就是投资(资金)的收益率,它表明了项目对所占用资金的一种恢复(回收)能力,项目的内部收益率越高,说明该项目的经济性也就越好。
换句话说,如果按利率i=IRR计算各年的净现金流量,在寿命期内各个时点,项目始终处于“偿还”未被收回的投资的状态,只有到了寿命期结束的时点,才偿清全部投资。将项目内部收益率的这种投资 “偿还”过程和结果按某一折现率折现为净现值时,则项目的净现值必然等于零。
由于项目的这种“偿付”能力完全取决于项目内部,故有“内部收益率”之称谓。
例:按上例的净现金流量及计算求得的内部收益率IRR=12.4%,计算和分析收回全部投资的过程。
上述例题表明投资回收过程:在项目寿命期内5年的各个时点上,每个时点上均存在未收回的投资(即,项目始终处于“偿还”未被收回的投资的状态)。只有到了寿命期结束的时点,才偿清全部投资。
五、内部收益率的优缺点
内部收益率指标优点:
①内部收益率法比较直观,概念清晰、明确,并可直接表明项目投资的盈利能力和反映投资使用效率的水平。
②内部收益率是内生决定的,即由项目的现金流量系统特征决定的,不是事先外生给定的。
内部收益率指标缺点:
①内部收益率指标计算繁琐,对于非常规项目有多解和无解问题,分析、检验和判别比较复杂。
②计算中存在着假设。即项目寿命期内各期的现金流量必须按照内部收益率进行再投资。
③内部收益率法适用于独立方案的经济评价和可行性判断,但多方案分析时,一般不能直接用于比较和选优。
*六.外部收益率ERR-----对IRR的进一步分析
内部收益率指标包涵了这样的再投资假设:项目各年的净收益要按IRR再投资(即投资于项目内部)。
外部收益率是指投资的未来值与再投资的净收益累计值相等时的收益率。
假设项目各年的净收益按i0再投资(即投资于项目外部),即:

——外部收益率ERR定义式
判别准则:
ERR指标用于评价投资方案经济效果时,需要与基准折现率i0比较。ERR ≥i0时,项目可以接受; ERR< i0时,项目应予拒绝。
七、差额(增量)内部收益率∆IRR
差额内部收益率∆IRR是指根据增量净现金流计算的差额净现值为零时的收益率。
差额内部收益率的方程式为:

式中:
∆IRR——A、B方案的差额内部收益率
差额内部收益率定义的另一种表述方式是:两互斥方案净现值(或净年值)相等时的折现率。其计算方程式也可以写成:
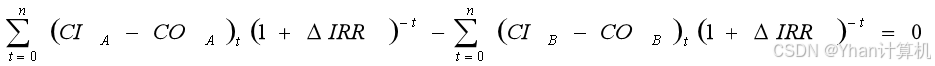

求解, ∆IRR的结果是一样的。这里∆IRR并不等于两方案IRR之差。 用差额内部收益率比选方案的判别准则是:若∆IRR≥i0(基准折现率),则投资(现值)大的方案为优;若∆IRR<i0,则投资(现值)小的方案为优。
例:用差额内部收益率法( △IRR )比选下表所列两方案,i0=10%。
解:
令△NPV= -20000+10000(P/F, △IRR,1)+10000(P/F, △IRR,2) + 10000(P/F, △IRR,3) = 0
当△IRR =20%时, △NPV=1064;△IRR =25%时, △NPV=-1839
△IRR=22% > i0,选B方案.
第四节 投资回收期法
投资回收期是指项目投产以后,用每年所获得的净收益回收全部投资所需要的时间,一般以年为单位。 根据是否考虑资金时间价值的影响,投资回收期可分为:静态投资回收期和动态投资回收期。
一、静态投资回收期
1. 定义:投资回收期(Pay back period)又称投资返本期,是指从项目投建之日起,用项目各年的净收入(年收入减年支出)将全部投资回收所需要的期限。
2.表达式

式中:
CIt——第t年的现金流入
COt——第t年的现金流出(包括投资)
NCFt——第t年的净现金流量, NCFt=(CI-CO)t
Tp——静态投资回收期
3.静态投资回收期的表格计算方法
对于各年净收入不同的项目,投资回收期通常用列表法求解,见下表。

根据表格法,计算静态投资回收期的实用公式为:

式中,T为项目各年累计净现金流量首次出现正值或零的年份。
4.静态投资回收期的判据
运用静态投资回收期指标评价技术方案时,需要与基准投资回收期相比较。
若![]() ,则方案可以考虑接受;若
,则方案可以考虑接受;若![]() ,则方案应予拒绝。
,则方案应予拒绝。
例:某项目的投资及收入、支出表,单位:万元
计算静态投资回收期的实用公式为:
解:
5.关于静态投资回收期的几点说明
(1)静态投资回收期的特点
静态投资回收期的优点:
①概念清晰,简单易行,直观,宜于理解;
②不仅在一定程度上反映了技术方案的经济性,而且反映了技术方案的风险大小和投资的补偿速度;
③既可判定单个方案的可行性(与T0比较),也可用于方案间的比较(判定优劣)。
静态投资回收期的缺点:
①没有反映资金的时间价值;
②由于它舍弃了方案在回收期以后的收入和支出情况,故难以全面反映方案在整个寿命期内的真实效益;
③没有考虑期末残值。
④方案的投资额相差较大时,比较的结论难以确定!
(2)基准投资回收期T0
不同地区、行业、时期,T0都有所区别。如表(基准投资收益率、基准投资回收期)
(3)投资、收益的计算范围
投资:
观点之一,只包括固定资产投资
观点之二,包括固定资产投资和流动资金投资(垫付)
收益:
观点之一,税前净收益
观点之二,税后净收益
处理原则:与T0一致、方案间一致。
(4)关于投资回收期的起点
观点之一,从贷款之日起(更合理)
观点之二,从投资之日起(可行性研究规定)
观点之三,从投产之日起(个别观点)
(5)投资回收期与折旧期的区别
投资回收期:反映了方案的盈利能力,与各年的实际收益有关,收益大、回收快,回收期就短。
折旧期:反映了设备(固定资产)的折旧寿命(与设备的盈利能力无关)与折旧方法、设备投资、寿命、国家规定等有关。
二、动态投资回收期
为了克服静态投资回收期未考虑资金时间价值缺点,在投资项目评价中有时采用动态投资回收期。动态投资回收期是能使下式成立的。
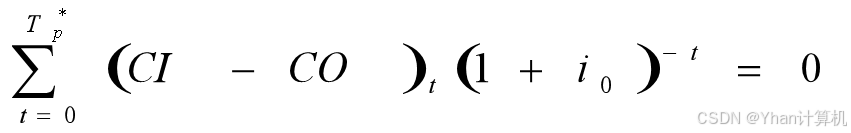
用动态投资回收期![]() 评价投资项目的可行性,需要与基准投资回收期
评价投资项目的可行性,需要与基准投资回收期![]() 相比较。判别准则为:若
相比较。判别准则为:若![]() ,则项目可以被接受,否则应予以拒绝。
,则项目可以被接受,否则应予以拒绝。
用上例的数据,贴现率为10%,单位:万元 求解动态投资回收期?
解:
计算动态投资回收期的实用公式为:
计算静态投资回收期的实用公式为:
动态投资回收期法优缺点:
优点:
投资回收期指标直观、简单,直接表明投资需要多少年才能回收,便于为投资者衡量风险。
缺点:
没有反映投资回收期以后的方案运行情况,因而不能全面反映项目在整个寿命期内真实的经济效果。所以投资回收期一般用于粗略评价,需要和其他指标结合起来使用。
三、增量投资回收期
指一个方案比另一个方案多追加的投资,用两个方案的年费用的节约额(或超额的年收益)来补偿所需的时间。计算公式为:

式中:投资额I2>I1且年费用C2<C1。
判断准则: 若ΔT≤Tb,增量投资有效,投资大的方案较优; 若ΔT>Tb,增量投资无效,投资小的方案较优。
拟建一个机械加工车间,有三个方案可供选择,资料如下,假定工业部规定Tb=5年,问哪个方案最好。
方案1:I1=1000,C1=1400
方案2:I2=1200,C2=1300
方案3:I3=1500,C3=1250
解:
方案2是最优方案。
第五节 其它指标评价法
一、投资收益率
投资收益率——是指项目在正常生产年份的净收益与投资总额的比值,是考察项目单位投资盈利能力的静态指标。计算公式为:

其中:年利润总额=年销售收入-年销售税金及附加-年总成本费用
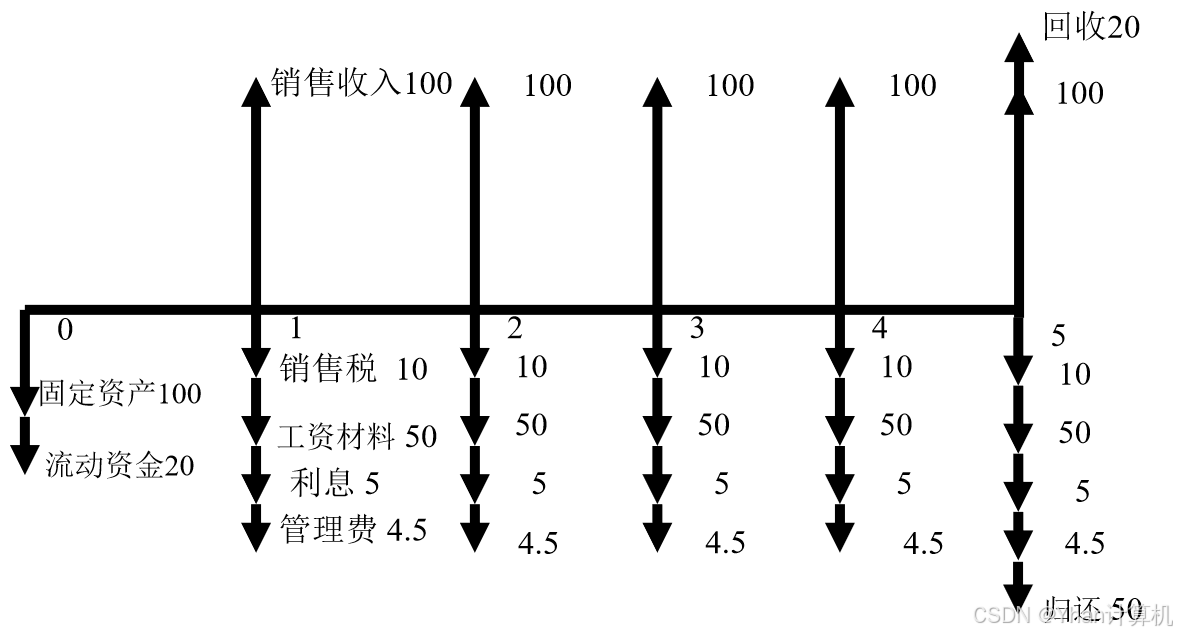
例:某项目总投资120万(固定资产100万,流动资产20万),全部为自有资金,寿命期5年,试求各年税后利润、投资利润率以及净现值率?i=10%
年折旧=100/5=20万元
年利润总额=销售收入100 -销售税10 -工资30-材料20-折旧20 –管理费用6 =14万元
年所得税 = 14×33%=4.62万元
税后利润 =14 -4.62 =9.38万元
年净现金流入 =100 –10 –30 – 20 –6 – 4.62 =29.4万元
净现值NPV = -120+29.4(P/A,10%,5)+20(P/F,10%,5)= 3.9
净现值率NPVR = 净现值/总投资的现值 = 3.9 / 120 = 3.3%
投资利税率——是考察项目单位投资对国家积累的贡献水平。其计算公式为:

其中:年利税总额=年销售收入– 年总成本费用
例:求利税总额、投资利税率以及净现值率?(i=10%)
年折旧=100/5=20万元
年利税总额=销售收入100 -折旧20 -工资30-材料20 –管理费用6 =24万元
净现金流入 =100 –10 –30 – 20 – 4.62 – 6=29.4万元
净现值NPV = -120+29.4(P/A,10%,5)+20(P/F,10%,5)= 3.9
净现值率NPVR = 净现值/总投资的现值= 3.9 / 120 = 3.3%
资本金利润率——反映投入项目的资本金的盈利能力,计算公式为:

例:上例中假设借款50万元,分别求税后利润,资本金利润率以及净现值率?(i=10%)
年折旧=100/5=20万元
年利润总额=销售收入100 -销售税10 -工资及材料费50-利息5-折旧20 –管理费用4.5=10.5万元
年所得税 = 10.5×33%=3.5万元
税后利润 = 10.5 - 3.5 =7万元
例:上例中假设借款50万元,分别求税后利润,资本金利润率以及净现值率?(i=16.6%)
年折旧=100/5=20万元
年利润总额=销售收入100 -销售税10 -工资及材料费50-利息8.3-折旧20 –管理费用4.5=11.7万元
例:上例中假设借款50万元,分别求税后利润,资本金利润率以及净现值率?(i=20%)
年折旧=100/5=20万元
年利润总额=销售收入100 -销售税10 -工资及材料费50-利息10-折旧20 –管理费用4.5=10万元
二、效益/费用比率指标
定义:通过计算公用事业项目投资方案的净效益与净费用的比值来评价方案。
计算公式:效益-费用比(B-C比)=净效益现值(年值)/净费用现值(年值)
评价标准:B-C比>1方案可行,B-C比<1方案不可行。
注意事项:
(1)一般适用于非盈利的公用事业项目。
(2)采用的折现率是公用事业资金的基准收益率或基金的利率。
(3)一般不能简单地根据B-C大小来选择最优方案,而应采用增量B-C比的比较法。
△ B-C>1说明B方案多投入的资金是有效的,因此投入大的方案为优
第六节 备选方案的经济性评价方法
一、备选方案及其类型
从各种备选方案中筛选最优方案的过程实际上就是决策的过程。合理的经济决策过程包括两个主要的阶段:
一是探寻各种解决问题的方案(这实际上是创新活动)。
二是对不同方案作经济衡量和比较,称之为经济决策。由于经济效果是评价和选择的主要依据,所以决策过程的核心问题就是对不同备选方案经济效果进行衡量和比较。
1、独立型——是指各个方案的现金流量是独立的,不具有相关性,且任一方案的采用与否都不影响其它方案是否采用的决策。
2、互斥型——是指各方案之间具有排他性,在各方案当中只能选择一个。
3、混合型——是指独立方案与互斥方案混合的情况。
二、互斥方案的经济评价方法
1.寿命期相等的互斥方案经济评价方法
不仅要进行方案本身的“绝对效果检验”,还需进行方案之间的“相对经济效果检验”。 通过计算增量净现金流量评价增量投资经济效果,也就是增量分析法,是互斥方案比选的基本方法。评价的常用指标:NPV、IRR、△NPV、△IRR。
现有A、B两个互斥方案,寿命相同,各年的现金流量如表所示,试评价选择方案(i0=12%)。
解:净现值法
∵增量投资方案B-A可行,
∴B比A方案好。
结论: 采用净现值指标比选互斥方案时,判别准则为:净现值最大且大于零的方案为最优方案。
例:现有A、B 两个互斥方案,寿命相同,各年的现金流量如表所示,试评价选择方案(i0 =12%)
解:
△NPVB-A= -10+2(P/A,12%,10)=1.3(万元)
令-10+2(P/A,△IRR,10)= 0
可解得:△IRR = 15%。
因此,增加投资有利,投资额大的B方案优于A方案。
例:为什么A方案的内部收益率大,却认为B方案比A方案好呢?(i0=12%)
结论:采用内部收益率IRR指标比选两个或两个以上互斥方案时,只能用增量内部收益率△IRR来判断。
IRR最大并不能保证项目比选结论的正确性。只有采用增量内部收益率△IRR指标才能保证比选结论的正确性。
采用△IRR的判别准则是:若△IRR≥i0(基准收益率),则投资大的方案为优;若△IRR<i0,则投资小的方案为优。
采用NPV指标比选互斥方案时,判别准则为:NPV最大且大于零的方案为最优方案。
采用NAV,即NAV最大且大于零的方案为最优方案。
采用费用现值PC或费用年值AC指标,其判别准则为:PC或AC最小的方案为最优方案。
例:某厂拟用 40 000元购置一台八成新的旧机床,年费用估计为 32 000元,该机床寿命期为 4年,残值 7 000元。 该厂也可用 60 000元购置一台新机床,其年运行费用为 16000元,寿命期也为 4年,残值为 15 000元。 若基准收益率为 10%,问应选择哪个方案?
PC法:
∴新比旧好。
AC法:
2.寿命期不相等的互斥方案经济性评价方法
最小公倍数法(方案重复法)
以各备选方案的寿命周期的最小公倍数作为比选的共同期限,假定各个方案均在这样一个共同的期限内反复实施,对各个方案分析期内各年的净现金流量换算到现值(即NPV法),按最小公倍数进行重复计算,直到分析期结束。
例: A、B两个互斥方案各年的现金流量如表 所示,基准收益率i0=10%,试比选方案。
解:(净年值法)
用净年值(NAV )评价两方案:
NAVA = -10 ( A / P,10%,6) + 3 +1.5 ( A/F,10%,6)= 0.90 (万元)
NAVB = -15 ( A/P,10%,9) + 4 + 2 ( A/F,10%,9)= 1.54(万元)
所以, B优于A。
解:(最小公倍数法)
NPVA = -10-10(P/F,10%,6)-10(P/F,10%,12)+3(P/A,10%,18)+1.5(P/F,10%,6)
+1.5(P/F,10%,12)+1.5 (P/F,10%,18) =7.37 >0
NPVB= -15-15(P/F,10%,9)+4(P/A,10,18)+2(P/F,10%,9)+2(P/F,10%,18) = 12.65 > 0 ∴ B比A好
是针对寿命期不同的互斥方案,直接选取一个适当的分析期作为各个方案共同的研究期,通过比较各个方案在该研究期内的净现值NPV(或者PC)来比选方案。 研究期的选择一般以各方案中寿命最短方案为比较的研究期。这种方法计算简便,而且可以避免重复性假设。
研究期法
研究期法涉及寿命期结束后,方案的未使用价值的处理问题。其处理方式有三种:
第一种考虑方案研究期以外未使用价值;
第二种不考虑方案研究期以外未使用价值;
第三种预测方案未使用价值在研究期末的价值,并作为现金流入量计算。
例:A、B两个互斥方案各年的现金流量如表 所示,基准收益率i0=10%,试比选方案。
解:方法一,考虑研究期以外方案未利用价值
NPVA= -10+3 (P/A,10%,6) +1.5(P/F,10%,6) =3.9>0
NPVB= -15(A/P,10%,9) (P/A,10%,6) +4 (P/A,10%,6)+2(A/F,10%,9) (P/A,10%,6) =6.70>0 ∴ B比A好
解:方法二,不考虑研究期结束方案未利用价值
NPVA= -10+3 (P/A,10%,6) +1.5(P/F,10%,6) =3.9>0
NPVB= -15+4 (P/A,10%,6) =2.42>0
∴ A比 B好
解:方法三,预计研究期结束方案未利用价值为4万元
NPVA= -10+3 (P/A,10%,6)+1.5(P/F,10%,6)=3.9>0
NPVB= -15+4 (P/A,10%,6) + 4(P/F,10%,6)=4.678>0
∴ B 比 A好
独立方案的经济评价方法
有资源制约条件下独立方案的比选,一般将可行的方案组合列出来,每个方案组合可以看成是一个满足约束条件的互斥方案。因此,有约束条件的独立方案的选择可以通过方案组合转化为互斥方案的比选,评价方法等同互斥方案比选方法。
例:独立方案A、B、C的投资额分别为100万元、70万元和120万元,经计算A、B、C方案的NAV分别为30万元、27 万元和32 万元,如果资金有限,投资额不超过250万元,问如何选择方案?
即选择A和C,可以使有限资金达到最佳利用,净年值总额为62万元
例:某制造厂考虑三个投资计划。在5年计划期中,这三个投资方案的现金流量情况如下表所示(该厂的最低希望收益率为10%)。
(1)假设这三个计划是独立的,且资金没有限制,那么应选择哪个方案或哪些方案?
(2)在(1)中假定资金限制在160000元,试选最好方案。
(3)假设A、B、C是互斥的,试用增量内部收益率法选出最合适的投资计划,增量内部收益率说明什么意思?
解:(1)假设这三个计划是独立的,且资金没有限制,那么应选择哪个方案或哪些方案? NPVA=-65000+18000(P/A,10%,5) +12000(P/F,10%,5) =10688 NPVB=-58000+15000(P/A,10%,5) +10000 (P/F,10%,5) =5074 NPVC=-93000+23000(P/A,10%,5) +15000(P/F,10%,5) =3506
因此, 三个方案都应选择。
解:(2)假定资金限制在160000元,试选最好方案。
当资金限制在160000元,应选择A+B 方案。
解:(3)假设计划A、B、C是互斥的,试用增量内部收益率法来选出最合适的投资计划,增量内部收益率说明什么意思?
令NPVA-B=-7000+3000(P/A,△IRR,5) +2000(P/F,△IRR,5)=0
i=35%时, NPVA-B=846.6
i=40%时, NPVA-B=-523.2
△IRRA—B=35.2%>10%,A优于B




































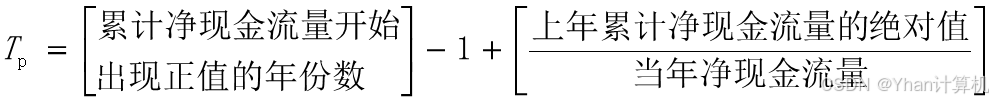







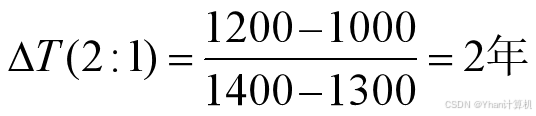






























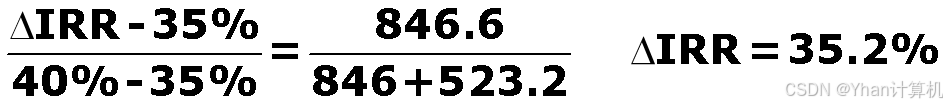


















 123
123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










