vslam学习：第二章作业

最新推荐文章于 2024-07-19 15:45:46 发布

m0_46247793

最新推荐文章于 2024-07-19 15:45:46 发布

阅读量81

点赞数

分类专栏： vslam 文章标签：算法自动驾驶 c++

本文链接：https://blog.csdn.net/m0_46247793/article/details/133857395

版权

vslam 专栏收录该内容

1 篇文章 0 订阅

订阅专栏

熟悉Eigen矩阵运算

设线性方程 Ax = b，在 A 为方阵的前提下，请回答以下问题：

1.在什么条件下，x 有解且唯一？

当方程组的系数矩阵A的秩与方程组增广矩阵[A|B]的秩相等时有解，且当R(A)=R(A,B)=n时方程有唯一解,n为方程组中未知数个数。

2.高斯消元法的原理是什么？

通过初等行变换，将线性方程组的增广矩阵转化为行阶梯矩阵，然后回代求出方程的解。

3.QR 分解的原理是什么？

把矩阵分解成一个列向量正交矩阵与一个上三角矩阵的积，原理是将矩阵每个列作为一个基本单元，将其化为正交的基向量，与在这个基向量上的投影长度的QR分解，经常用来解决最小回归问题。

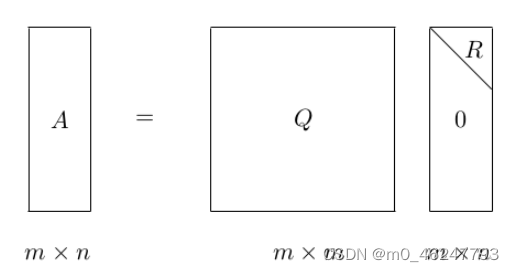
4.Cholesky 分解的原理是什么？

把一个实对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。一个实对称矩阵A正定，即存在可逆矩阵L，使得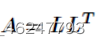

5.编程实现 A 为 100 × 100 随机矩阵时，用 QR 和 Cholesky 分解求 x 的程序。你可以参考本次课用到的 useEigen 例程。

按照camke工程管理方式建立工程：

CMakeLists.txt建立如下：

cmake_minimum_required(VERSION 3.10)
project(LinearEquationSolver)
# 查找Eigen库
find_package(Eigen3 REQUIRED)
# 添加可执行文件
add_executable(${PROJECT_NAME} src/main.cpp)
# 链接Eigen库
target_link_libraries(${PROJECT_NAME} Eigen3::Eigen)

main.cpp具体代码如下：

#include <iostream>
#include <ctime>
using namespace std;

#include <Eigen/Core>
//稠密矩阵的代数运算
#include <Eigen/Dense>
#include <Eigen/QR>
#include <Eigen/Cholesky>
using namespace Eigen;

int main(int argc,char** argv)
{
        time_t time,start,end;
        //声明一个100*100的随机矩阵m_11
        Eigen::Matrix<float,Eigen::Dynamic,Eigen::Dynamic>m_11=Eigen::Matrix<float,Eigen::Dynamic,Eigen::Dynamic>::Random(100,100);
        //产生对称矩阵,因为cholesky分解需要对正定对称矩阵进行
        m_11 = m_11.transpose() * m_11;
        //计算行列式
        cout<<"Matrix determination:"<<m_11.determinant()<<endl;
        //声明一个100*1的向量v_11
        Eigen::Matrix<float,Eigen::Dynamic,Eigen::Dynamic>v_11=Eigen::Matrix<float,Eigen::Dynamic,Eigen::Dynamic>::Random(100,1);
        //声明未知的x
        Eigen::Matrix<float,100,1>x;
        cout<<"A="<<m_11<<endl;
        cout<<"b="<<v_11<<endl;
        //QR分解计算x
        start = clock();
        x=m_11.colPivHouseholderQr().solve(v_11);
        end=clock();
        time=end-start;
        cout<<"X="<<x<<endl;
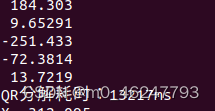
        cout<<"QR分解耗时："<<time<<"ms"<<endl;
        // Cholesky 分解计算x
        start=clock();
        x=m_11.llt().solve(v_11);
        end=clock();
        time=end-start;
        cout<<"X="<<x<<endl;
        cout<<" Cholesky 分解耗时："<<time<<"ms"<<endl;
}

最后运行结果：

矩阵论基础

1. 什么是正定矩阵和半正定矩阵？

正定矩阵：特征值均大于零（都是正数）

半正定矩阵：特征值可以是零或正数（不小于零）

2.对于方阵A，它的特征值是什么？特征向量是什么？特征值一定是实数吗？如何计算一个矩阵的特征值？

特征值：如果等式:Av= λv，那么 λ就是矩阵A的一个特征值。

特征向量：如上等式中的向量v就是对应于特征值 λ的特征向量。

特征值的实数性质：特征值可以是实数或复数，取决于矩阵A的性质；对于实对称矩阵，其特征值一定是实数；但对于一般的矩阵，特征值可以是复数。

计算特征值和特征值向量：通过求解特征方程（|A - λI| = 0）来找到特征值λ。其中，I是单位矩阵。然后，将每个特征值代入方程 A * v = λ * v 来求解对应的特征向量。

3.什么是矩阵的相似性？相似性反映了什么几何意义？

两个方阵A和B被称为相似矩阵，如果存在一个可逆矩阵P，使得后面的关系成立：B = P⁻¹ * A * P

几何意义：

共享特征值和特征向量：如果两个矩阵A和B是相似的，它们具有相同的特征值，虽然特征向量可能会发生变化。这意味着它们在一些方向上发生了类似的变换，只是在不同的坐标系下。
几何形状保持：相似矩阵之间的变换可以被视为一个几何变换。当矩阵相似时，它们所表示的线性变换保持了某种几何形状，例如，保持了直线、平面或其他几何对象。
对角化的关系：如果一个矩阵A可以对角化（变为对角矩阵D），即 A = P⁻¹ * D * P，其中D是对角矩阵，那么与A相似的矩阵B也可以对角化为相同的D。

4.矩阵一定能对角化吗？什么样的矩阵能保证对角化？不能对角化的矩阵能够形成什么样的形式（Jor-dan标准形）？

不是所有的矩阵都能对角化，矩阵能够对角化的前提是它有足够多的线性无关的特征向量；一个方阵能够对角化，当且仅当它有n个线性无关的特征向量，其中n是矩阵的维度。

对于不可对角化的矩阵它们能够形成一种Jordan标准形。Jordan标准形是一个分块对角矩阵，其特征值在对角线上，而其上方的第一条次对角线上有1，其他元素均为零。

5.奇异值分解（SVD）是什么意思？

一种矩阵分解方法，将一个矩阵分解为三个矩阵的乘积形式：A = UΣV^T

6.矩阵的伪逆是什么意思？莫尔----彭多斯逆是如何定义的？怎么计算一个矩阵的伪逆？

矩阵的伪逆是广义逆矩阵的一种，用于解决矩阵不满秩或不可逆的情况下的线性方程组。

莫尔-彭若斯（Moore-Penrose）逆是矩阵的一种特殊的伪逆，具体定义如下：

对于一个 m × n 的矩阵 A，其莫尔-彭若斯逆（A的伪逆）通常记为 A^+，满足以下条件：

如果 A 是一个可逆矩阵，那么 A^+ 就等于 A 的逆矩阵，即 A^+ = A⁻¹。
如果 A 是一个非方阵，那么 A^+ 就是 A 的左逆矩阵和右逆矩阵的平均，即 A^+ = (A^T A)^⁻¹ A^T，其中 A^T 是 A 的转置。

莫尔-彭若斯逆具有一些重要性质，如：

(AA^+A) = A
(A^+AA^+) = A^+
(AA^+)^T = AA^+
(A^+A)^T = A^+A

计算矩阵的伪逆可以使用多种方法，其中最常用的是奇异值分解（SVD）：

对于一个 m × n 的矩阵 A，它的奇异值分解为 A = UΣV^T，其中 U 和 V 是酉矩阵（或正交矩阵），Σ 是一个对角矩阵，其对角线上的元素是矩阵 A 的奇异值。

矩阵 A 的莫尔-彭若斯逆为 A^+ = VΣ^+U^T，其中 Σ^+ 是 Σ 的伪逆对角矩阵，即将 Σ 的每个非零奇异值取倒数，然后对角线上的元素求转置。

7.对于超定方程：Ax=b且A不可逆时，我们通常计算最小二乘解：x=arg min||Ax-b||。线性方程的最小二乘解在代数意义上是可以解析写出来。请回答以下小问题：

(a)在b≠0时，x的解是什么形式?事实上，我们可以对A求奇异值或对于A^TA求特征值。请阐述两者之间的关系。

由于矩阵A不可逆且b≠0,使用最小二乘法结合矩阵的伪逆可以找到一个近似解x = VΣ^+U^Tb

对于一个 m × n 的矩阵 A，它的奇异值分解为 A = UΣV^T，其中 U 和 V 是酉矩阵，Σ 是一个 m × n 的矩阵，其对角线上的元素是 A * A^T 或 A^T * A 的特征值的平方根。

A * A^T 的非零特征值是 A 的奇异值的平方。
A^T * A 的非零特征值是 A 的奇异值的平方。
A * A^T 的非零特征向量可以通过 A^T * A 的特征向量通过变换 P^(-1) 得到。

(b)当b=0时，我们希望求a 的非零解。请说明如何求解x。

计算矩阵 A 的零空间：
- 对矩阵 A 进行奇异值分解（SVD），得到 A = UΣV^T。
- 找到 A * A^T 的非零特征向量（零空间向量），它们对应于矩阵 A 的零空间。
提取非零解 x：
- 在 A * A^T 的非零特征向量中，选择一个特征向量作为非零解 x。

(c)请谈谈你对上述解法在几何意义上的理解。该问题为开放问题。

理论知识刚接触有点复杂，需要慢慢消化

在求解超定方程 Ax = 0 时，我们实际上在寻找在零空间中的非零向量 x。这些向量描述了 A 的线性变换如何将它们映射到零向量。这在应用中具有重要意义，比如在数据降维中，我们可以找到数据中存在的共线性或冗余信息。

几何运算练习

1.说明一个激光传感器下的看到的点应该如何计算它的世界坐标。

传感器坐标系和世界坐标系的定义：首先，需要定义激光传感器的坐标系和世界坐标系。

坐标变换：将传感器坐标系中的点转换到世界坐标系中。这涉及到旋转和平移变换，通常使用变换矩阵来表示。这个变换矩阵可以是从传感器坐标系到世界坐标系的旋转矩阵和平移向量的组合。

测量数据处理：激光传感器会返回一系列的距离测量值（通常是从传感器到物体的距离）。这些测量值需要通过传感器的内部校准和数据处理进行修正，以考虑传感器的特性，如光学畸变、噪声等。

计算世界坐标：对于每个传感器测量的点，使用之前计算得到的变换矩阵将传感器坐标转换为世界坐标。这样，你就可以得到在世界坐标系中的点的坐标。

2.取：qW R = [0.55, 0.3, 0.2, 0.2], tW R = [0.1, 0.2, 0.3]T，qRB = [0.99, 0, 0, 0.01], tRB = [0.05, 0, 0.5]T，qBL = [0.3, 0.5, 0, 20.1], tBL = [0.4, 0, 0.5]T , qBC = [0.8, 0.2, 0.1, 0.1], tBC = [0.5, 0.1, 0.5]T。现在假设相机传感器观察到自身坐标系下的点 [0.3, 0.2, 1.2]，请计算：

(a)这个点在激光系下的坐标；

(b)这个点在世界系下的坐标。

建立下面工程结构

其中main.cpp代码如下：

#include <iostream>
#include <Eigen/Dense>
#include <Eigen/Geometry>

int main(){

	Eigen::Quaterniond qWR(0.55,0.3,0.2,0.2);
	Eigen::Vector3d tWR(0.1,0.2,0.3);
	Eigen::Quaterniond qRB(0.99,0,0,0.01);
	Eigen::Vector3d tRB(0.05,0,0.5);
	Eigen::Quaterniond qBC(0.8,0.2,0.1,0.1);
	Eigen::Vector3d tBC(0.5,0.1,0.5);
	Eigen::Quaterniond qBL(0.3,0.5,0,20.1);
	Eigen::Vector3d tBL(0.4,0,0.5);
	Eigen::Vector3d point_camera(0.3,0.2,1.2);
	
	Eigen::Isometry3d T_WR(qWR);
	T_WR.pretranslate(tWR);
	Eigen::Isometry3d T_RB(qRB);
	T_RB.pretranslate(tRB);
	Eigen::Isometry3d T_BC(qBC);
	T_BC.pretranslate(tBC);
	Eigen::Isometry3d T_BL(qBL);
	T_BL.pretranslate(tBL);
	
	//Transform the point from camera to world
	Eigen::Vector3d point_world = T_WR.inverse() * point_camera;
	
	// Transform the point from world to robot
	Eigen::Vector3d point_robot = T_RB.inverse() * point_world;
	
	// Transform the point from robot to base station
	Eigen::Vector3d point_base = T_BL.inverse() * point_robot;
	
	// Transform the point from base station to laser
	Eigen::Vector3d point_laser = T_BC.inverse() * point_base;
	
	std::cout << "point in laser frame: " << point_laser.transpose() << std::endl;
	std::cout << "point in world frame: " << point_world.transpose() << std::endl;
	return 0;

}

Eigen::Quaterniond 是Eigen库中用于表示四元数（quaternion）的类。四元数是一种数学工具，通常用于表示旋转操作，尤其在三维空间中的旋转。

Eigen::Vector3d 是Eigen库中用于表示三维向量（vector）的类。它用于表示具有三个分量的向量，通常在三维空间中表示位置、方向或其他类型的三维数据。

Eigen::Isometry3d 是Eigen库中用于表示仿射变换（affine transformation）的类，特别是在三维空间中的变换。仿射变换是一种将点从一个坐标系转换到另一个坐标系的变换，包括平移、旋转和缩放等操作。

pretranslate() 方法将一个给定的三维平移向量添加到仿射变换的平移部分

工程管理CMakeLists.txt配置如下：

cmake_minimum_required(VERSION 3.12)
project(geometry)
find_package(Eigen3 REQUIRED)

# 添加可执行文件

add_executable(zqx_p main.cpp)

# 包含Eigen3头文件

target_include_directories(zqx_p PRIVATE ${EIGEN3_INCLUDE_DIRS})

# 设置构建目标文件输出路径

set(EXECUTABLE_OUTPUT_PATH ${CMAKE_SOURCE_DIR}/build)

最后得到计算的结果如下：

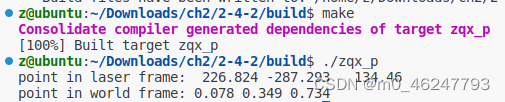
旋转的表达

1.设有旋转矩阵 R，证明 R^T* R = I 且 det R = +1^1。

2.设有四元数 q，我们把虚部记为 ε，实部记为 η，那么 q = (ε, η)。请说明 ε 和 η 的维度。

虚部 ε是一个三维向量，用来表示旋转轴在虚部的部分，通常由三维向量（x,y,z)表示。因此，虚部 ε的维度为3

实部 η是一个标量，用来表示旋转角度或缩放因子，通常由一个标量值表示，因此其维度为1。

3.定义运算 + 和 ⊕ 为：

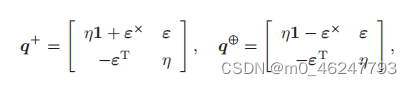
其中运算 × 含义与 ∧ 相同，即取 ε 的反对称矩阵（它们都成叉积的矩阵运算形式），1 为单位矩阵。请证明对任意单位四元数 q1, q2，四元数乘法可写成矩阵乘法：q1q2 = q1 +q2 (2) 或者q1q2 = q2 ⊕q1 (3)

罗德里格斯公式的证明

罗德里格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ，方向为 n，那么旋转矩阵 R 为：

R = cos θI + (1 − cos θ)nn^T + sin θn^

1.我们在课程中仅指出了该式成立，但没有给出证明。请你证明此式。

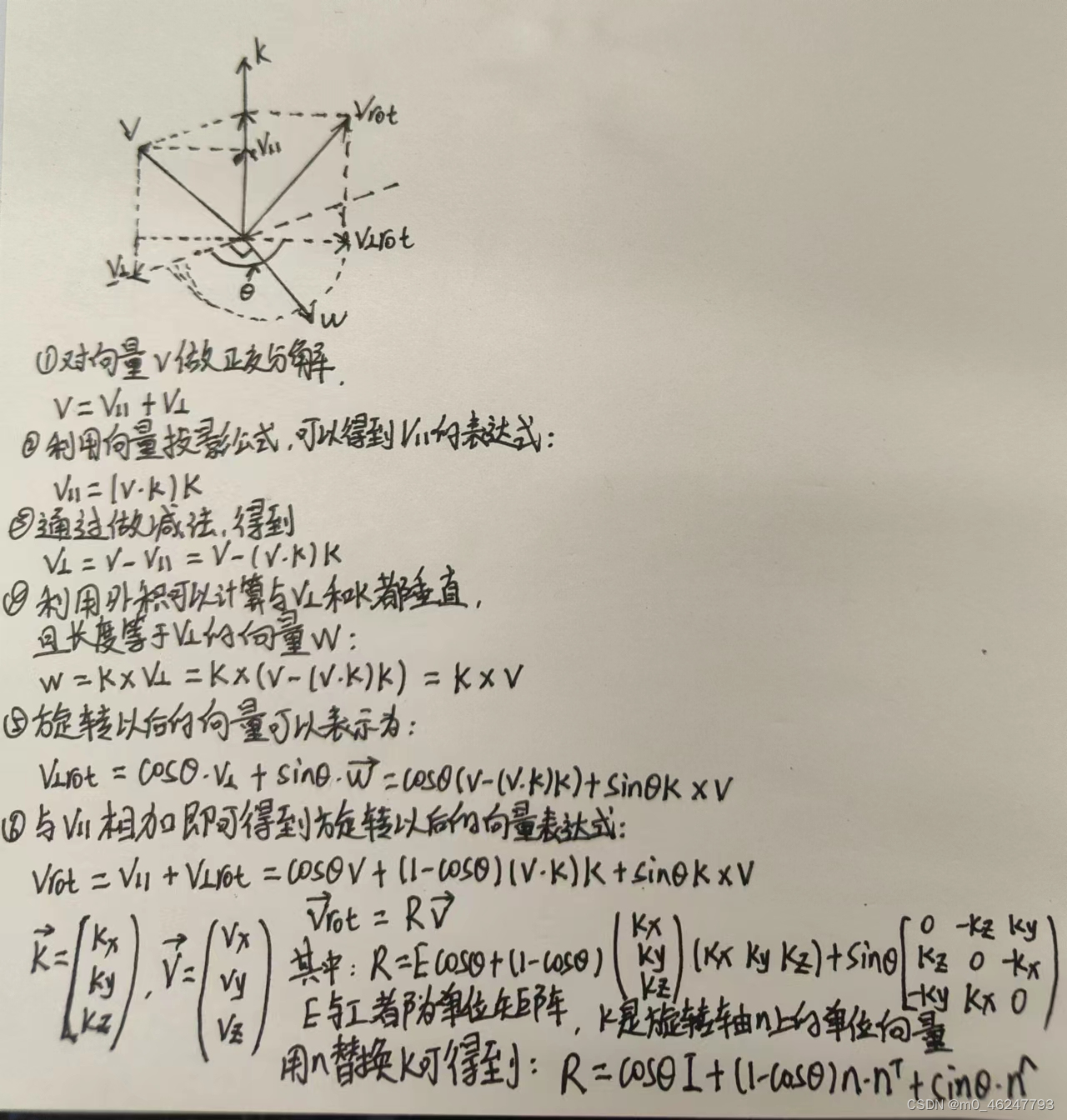
2.请使用此式请明 R^(−1) = R^T

四元数运算性质的验证

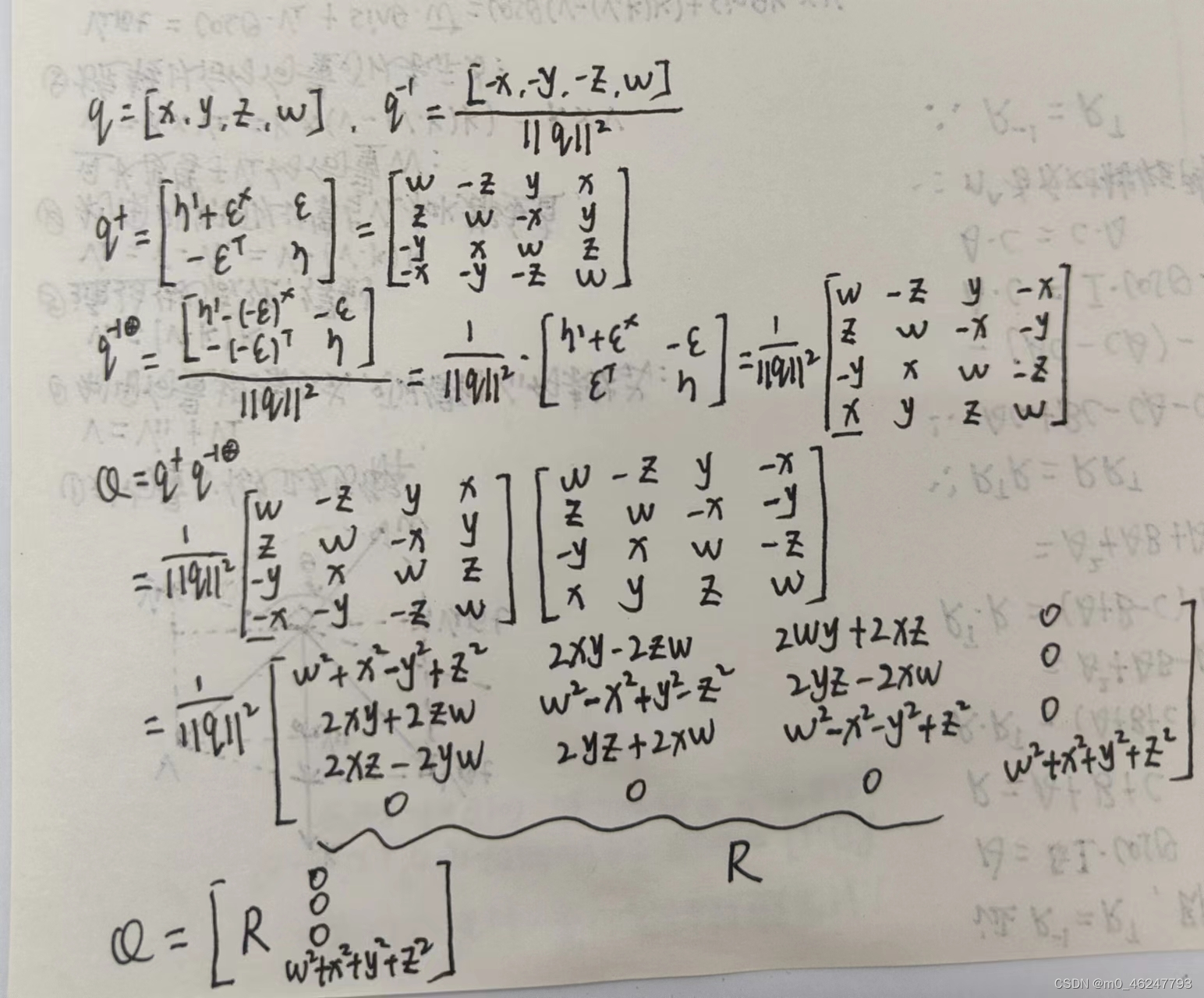
课程中介绍了单位四元数可以表达旋转。其中，在谈论用四元数 q 旋转点 p 时，结果为：p ′ = qpq^(−1)我们说，此时 p ′ 必定为虚四元数（实部为零）。请你验证上述说法。

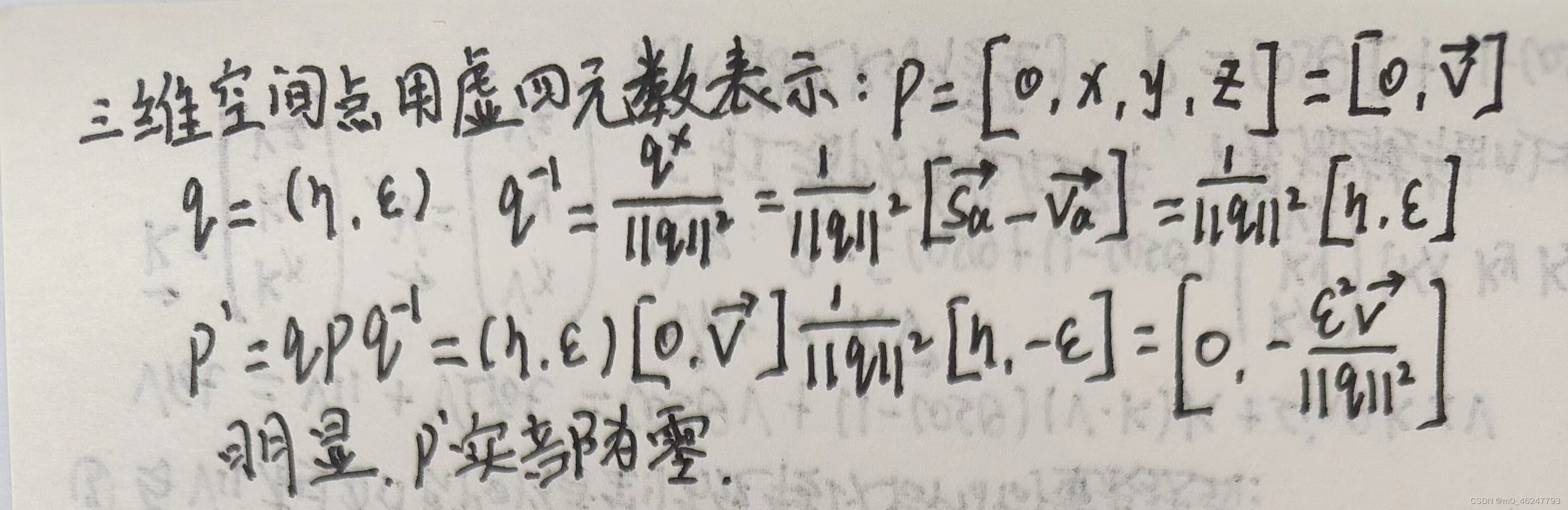
此外，上式亦可写成矩阵运算：p ′ = Qp。请根据你的推导，给出矩阵 Q。注意此时 p 和 p ′ 都是四元数形式的变量，所以 Q 为 4 × 4 的矩阵。

提示：如果使用第 4 题结果，那么有：

从而可以导出四元数至旋转矩阵的转换方式：

其中 Im 指取出虚部的内容。

m0_46247793

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
vslam学习：第二章作业

正定矩阵：特征值均大于零（都是正数）半正定矩阵：特征值可以是零或正数（不小于零）两个方阵A和B被称为相似矩阵，如果存在一个可逆矩阵P，使得后面的关系成立：B = P⁻¹ * A * P共享特征值和特征向量：如果两个矩阵A和B是相似的，它们具有相同的特征值，虽然特征向量可能会发生变化。这意味着它们在一些方向上发生了类似的变换，只是在不同的坐标系下。几何形状保持：相似矩阵之间的变换可以被视为一个几何变换。当矩阵相似时，它们所表示的线性变换保持了某种几何形状，例如，保持了直线、平面或其他几何对象。
复制链接

扫一扫