NIST测试续——详细版

NIST测试过程

• 双击Cygwin64 Terminal
  
• 输入assess.exe所在文件夹的绝对地址，注意要更改斜杠的方向，如果不改的话，找不到这个地址。
  
• 启动assess.exe，选择测试数据，这部分已在之前的博客中介绍过，不再详述。
  
  进行15个测试
  
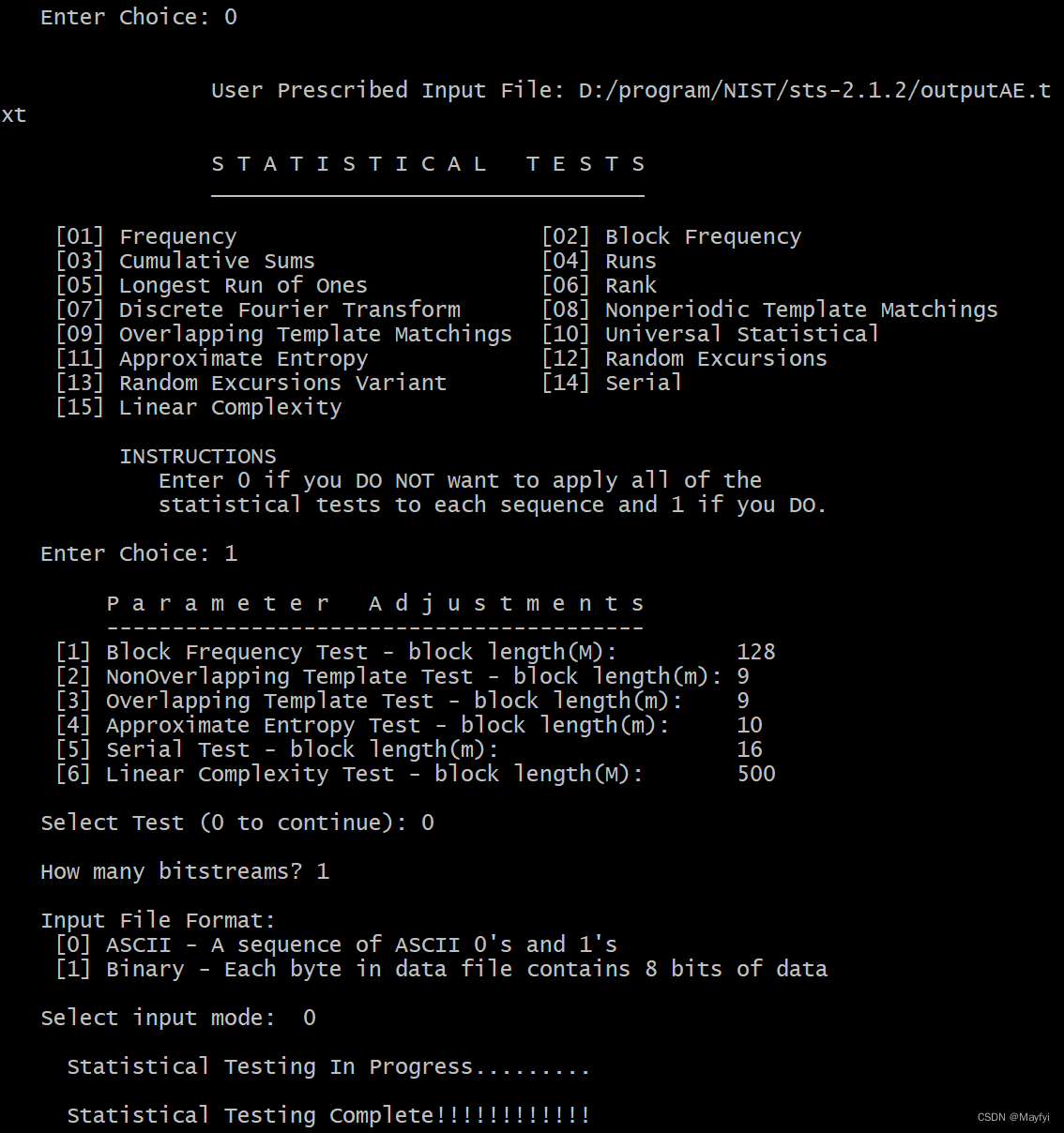
  NIST测试说明

1. 检验统计量用于计算总结针对零假设的证据强度的P-value值。对于这些测试，在给定测试评估的非随机性类型的情况下，每个P-value值是完美随机数发生器生成的序列随机性小于被测序列的概率。如果确定测试的P-value值等于1，则序列似乎具有完全随机性。若P-value值为零表示该序列似乎是完全非随机的。

2. 这些测试侧重于序列中可能存在的各种不同类型的非随机性，其中的一些测试可分解为各种子测试。

3. Frequency：测试的是序列中0，1的个数，随机序列中0和1的个数应该大致相等，其余检测是在该测试的基础上进行的，若通过该测试，被测序列是随机的。
   $$\text{P-value}=erfc(\frac{S_{obs}}{\sqrt{2}})$$
   $erfc$ is the complementary error function.
   
   
   the nth partial sum=序列中0，1个数的差值
   

4. Block Frequency：测试的是M位的子块中0，1的个数是否大致相等。M是每个块的大小，n是序列的总长，$N=\lfloor \frac{n}{M}\rfloor$.
   The block size M should be selected such that $M\ge 20$, $M\ge 0.01\ast n$, and $N\le 100$.
   $igamc$ is the incomplete gamma function for $Q=(a,x)$
   
   

5. Cumulative Sums：检验的依据是部分和的绝对值的最大值的绝对值，可被认为是随机游程（a random walk），对于随机序列，随机游程的偏移应该接近于零。对于某些类型的非随机序列，这种随机游程可能前期的偏移会很大。由于可以正着来计算部分和，也可以逆着，所以有两个值，一个是forward，一个是reverse。
   $z$ 是最大部分和，计算P-value。
   
   

6. Runs：此检验主要是看游程的总数，游程指的是一个没有间断的相同数序列，即游程或者是“1111„”或者是“0000„”。一个长度为k 的游程包含k 个相同的位。游程检测的目的是判定不同长度的“1”游程的数目以及“0”游程的数目是否跟理想的随机序列的期望值相一致。具体的讲，就是该检验手段判定在这样的“0”“1”子块之间的振荡是否太快或太慢。
   $\pi$是输入序列中“1”的比例。
   
   
   
   

7. Longest Run of Ones：该检验主要是看长度为M-bits的子块中的最长“1”游程。这项检验的目的是判定待检验序列的最长“1”游程的长度是否同随机序列的相同。注意：最长“1”游程长度上的一个不规则变化意味着相应的“0”游程长度上也有一个不规则变化，因此，仅仅对“1”游程进行检验是足够的。
   

8. Rank：整个序列的分离子矩阵的秩，此测试的目的是核对源序列中固定长度子链间的线性依赖关系。

9. Discrete Fourier Transform：本检验主要是看对序列进行分步傅里叶变换后的峰值高度。目的是探测待检验信号的周期性，以此揭示其与相应的随机信号之间的偏差程度。做法是观察超过 95%阈值的峰值数目与低于 5%峰值的数目是否有显著不同。

10. Non-overlapping Template Matching： 此检测主要是看提前设置好的目标数据串发生的次数。目的是探测那些产生太多给出的非周期模式的发生器。使用一个 m-bit 的窗口来搜素一个特定的 m-bit 模式。如果这个模式没有被找到，则窗口向后移动一位。如果模式被发现，则窗口移动到一发现的模式的后一位，重复前面的步骤继续搜素下一个模式。
    默认的模板中有148个templates，所以会有148个结果。

11. Overlapping Template Matching： 该检验主要是看提前设定的目标模块发生的数目。检验步骤同非重叠模块匹配检验方法大致一样，不同点在于，发现目标模块后，窗口仅向后移动1位，而后继续搜索。
    

12. Universal Statistical： 检验的重点是匹配模块之间的bit数。目的是检验序列能否在没有信息损耗的条件下被大大的压缩。一个能被大大压缩的序列被认为是一个非随机序列。
    需要注意的是，进行这个测试需要a long sequence of bits，不然的话，这个test无法通过。
    

13. Approximate Entropy：近似熵检验看的是整个序列中所有可能的重叠 m-bit 模式的频率。目的是将两相邻长度(m和m+1)的重叠子块的频数与随机情况下预期的频数相比较。
    

14. Random Excursions：该测试的重点是在累积和随机游程中恰好有K次访问的周期数。累积和随机游程是从(0,1)序列转移到适当的（-1,+1）序列后的部分和得出的。随机游程的循环由一系列随机采取的单位长度的步骤组成，这些步骤从原点开始并返回原点。此测试的目的是确定在一个周期内访问特定状态的次数是否偏离了人们对随机序列的预期。
    

15. Random Excursions Variant：该测试的重点是在累积和随机游程中访问（即发生）特定状态的总次数。此测试的目的是检测随机游程中对各种状态的预期访问次数的偏差。
    

16. Serial：整个序列中所有可能的重叠m-bit模式的频率，目的是判定$2^m$个m-bit重叠模式的数目是否跟随机情况下预期的值相近似。随机序列具有均匀性也就是说对于每个m-bit模式其出现的概率应该是一样的。当m=1时等价于频数检验。
    
    

17. Linear Complexity Test： 这个测试的重点是线性反馈移位寄存器（LFSR）的长度。这个测试的目的是确定序列是否复杂到足以被认为是随机的。随机序列的特点是有较长的LFSR。一个太短的LFSR意味着非随机性。
    

参考：博客一
博客二
NIST官方文档