【深层神经网络】深度学习专项课程学习记录3——多隐藏层神经网络解决图像二分类问题

最新推荐文章于 2023-09-03 21:02:21 发布

小飞狗狗

最新推荐文章于 2023-09-03 21:02:21 发布

阅读量486

点赞数

分类专栏：吴恩达深度学习文章标签：深度学习神经网络 python

本文链接：https://blog.csdn.net/m0_46314771/article/details/125450609

版权

吴恩达深度学习专栏收录该内容

11 篇文章 0 订阅

订阅专栏

学习目标

运用Numpy搭建多层深度神经网络实现图像二分类问题。还是之前的“cat”“not_a_cat”分类问题，这次试试L层神经网络的效果。

笔记

1.L层神经网络模型

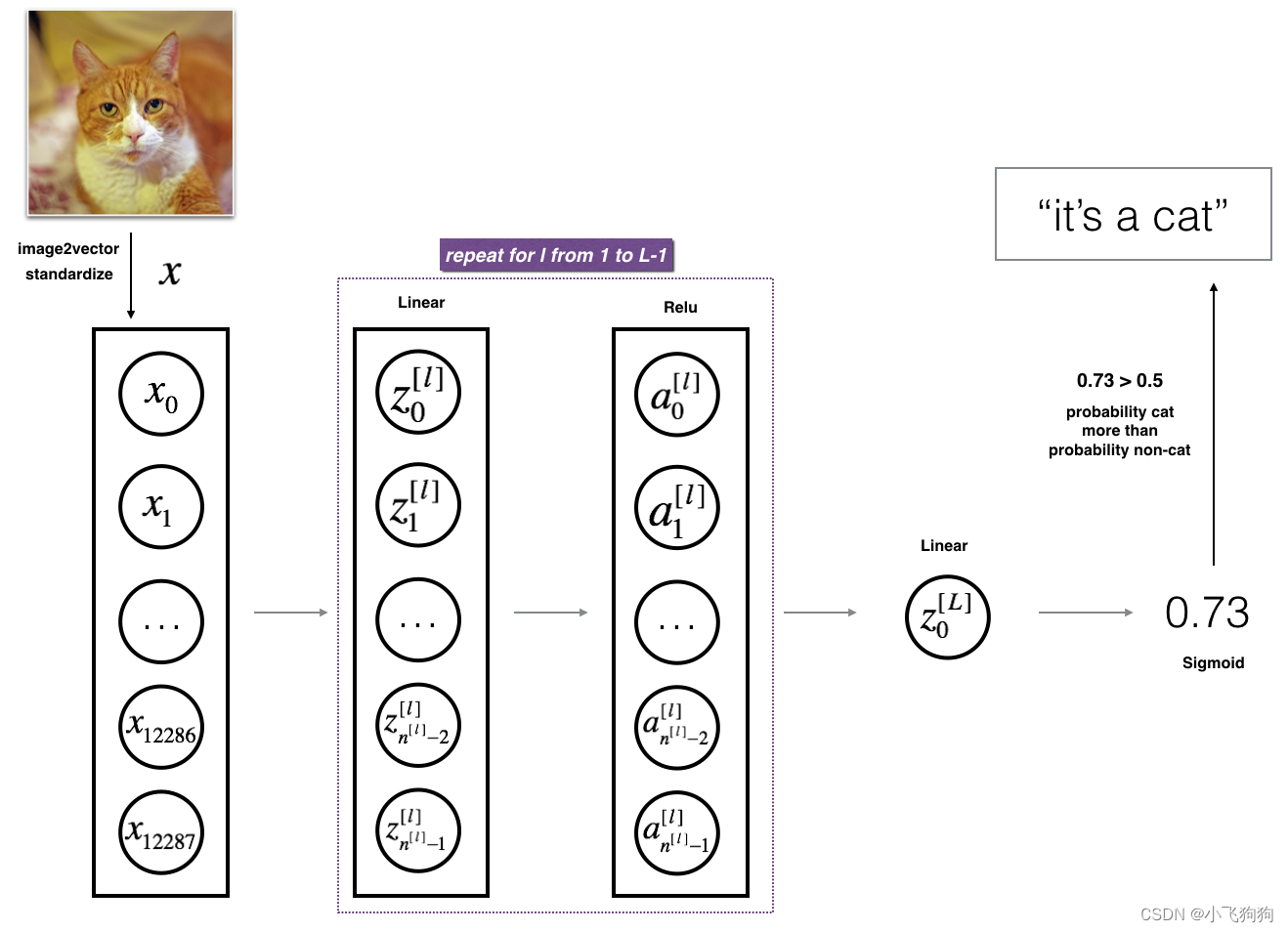
L层神经网络模型实现图像二分类问题

L层神经网络架构如上图所示，构建L层神经网络模型同样需要经过“参数初始化——正向传播——计算损失——反向传播——更新参数”的过程。与单隐藏层神经网络不同的是，L层神经网络具有L-1个隐藏层。该模型的超参数为：layers_dims，learning_rate，num_iterations。

# 示例
n_x = 12288 # 像素*像素*通道数，即num_px * num_px * 3
n_y = 1  #输出维度
layers_dims = [n_x,n_h,n_y] # [12288, 20, 7, 5, 1]是一个四层的模型，n_h表示隐藏层包含的神经元数量
learning_rate = 0.0075
num_iterations = 3000

总体上，经过整合的L层神经网络模型如下所示。可以看到主要包括五个函数：initialize_parameters_deep(layers_dims)、L_model_forward(X, parameters)、compute_cost(AL, Y)、L_model_backward(AL, Y, caches)和update_parameters(parameters, grads, learning_rate)。在下文的“模型拆解”部分会详细讲每个函数。

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):

    np.random.seed(1)
    costs = [] 
    
   	# 参数初始化
   	parameters = initialize_parameters_deep(layers_dims)
    
    # 循环（梯度下降）
    for i in range(0, num_iterations):
        
        # 正向传播: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        AL, caches = L_model_forward(X, parameters)
        
       	# 计算损失
       	cost = compute_cost(AL, Y)
        
        # 反向传播
        grads = L_model_backward(AL, Y, caches)
 
        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
                
        # 每100次迭代打印一次cost
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)
    
    return parameters, costs

上述过程用图表示为：
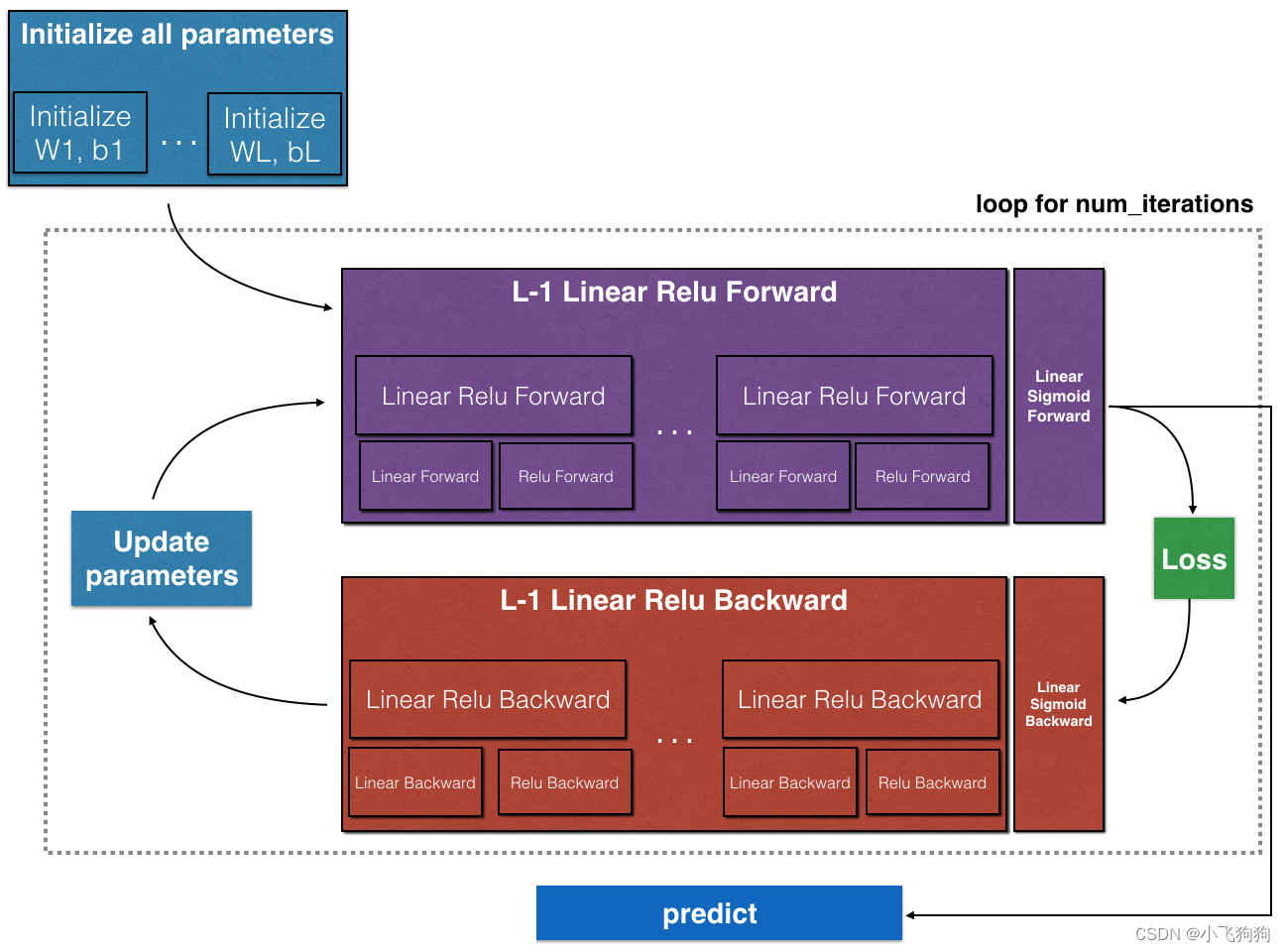
L层神经网络模型组成

2. 模型拆解

2.1 参数初始化——W,b

W采用随机初始化的方法，b采用零初始化。对于层l，W[l]的维度是（n[l]，n[l-1]），b[l]的维度是（n[l]，1）。

def initialize_parameters_deep(layer_dims):
    parameters = {}
    L = len(layer_dims) #L是神经网络的层数
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01 
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
        
    return parameters

2.2 正向传播

正向传播包括线性函数部分和激活函数部分。下面的代码首先定义了线性函数，然后在此基础上计算激活函数，最后定义L层神经网络模型的完整正向传播过程，其中：在1~（l-1）层使用relu作为激活函数，在输出层（L层）使用sigmoid作为激活函数。
线性函数部分：
$Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}$

其中 $A^{[0]} = X$ .

激活函数部分：
$A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})$
g可以是 $r e l u ()$ 或 $s i g m o i d ()$ :
$R E L U (Z) = m a x (0, Z)$
$\sigma(Z) = \sigma(W A + b) = \frac{1}{ 1 + e^{-(W A + b)}}$
注意： $s i g m o i d ()$ 往往用 $\sigma()$ 表示。

#定义正向传播的线性部分
def linear_forward(A, W, b):
    Z = np.dot(W,A) + b
    cache = (A, W, b)
    
    return Z, cache   

#进一步定义正向传播的线性激活
def linear_activation_forward(A_prev, W, b, activation):
    if activation == "sigmoid":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)
    
    elif activation == "relu":
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)

    cache = (linear_cache, activation_cache)

    return A, cache 

#进一步定义L层神经网络模型的完整正向传播过程
def L_model_forward(X, parameters):
    caches = []
    A = X
    L = len(parameters) // 2
    for l in range(1, L):
        A_prev = A 
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation="relu")
        caches.append(cache)
    AL, cache = linear_activation_forward(A,parameters['W' + str(L)], parameters['b' + str(L)], activation="sigmoid")
    caches.append(cache)
    return AL, caches

2.3 计算损失

此处用交叉熵损失函数，表达式如下：
$J=-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right))$

def compute_cost(AL, Y):
    m = Y.shape[1]
    cost = - 1/m * np.sum(Y * np.log(AL)+(1-Y)*np.log(1-AL))
    
    cost = np.squeeze(cost)     

    return cost

2.4 反向传播

首先初始化dAL，即 $\frac{\partial \mathcal{L}}{\partial A^{[L]}}$ ，公式用python表达为：

dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

然后计算L层的梯度，包括： $dZ^{[l]},dW^{[l]}, db^{[l]}, dA^{[l-1]}$ ，其中 $dZ^{[l]}$ 由激活部分的计算得到， $dW^{[l]}, db^{[l]}, dA^{[l-1]}$ 由线性部分的计算得到。
继续往前计算（l-1）~1层的梯度，每一层都得到对应的 $d Z, d W, d b$ 以及上一层的 $d A$ .

线性函数部分：
$dW^{[l]} = \frac{\partial \mathcal{J} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T}$
$db^{[l]} = \frac{\partial \mathcal{J} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}$
$dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]}$

激活函数部分：
$dZ^{[l]} = dA^{[l]} * g'(Z^{[l]})$
其中， $g ()$ 表示激活函数。这部分公式用python表示如下，sigmoid_backward()和relu_backward()是引用的。

dZ = sigmoid_backward(dA, activation_cache)
#或者
dZ = relu_backward(dA, activation_cache)

反向传播所用的函数全部代码如下：

def linear_backward(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]
    
    dW = 1/m * np.dot(dZ,A_prev.T)
    db = 1/m * np.sum(dZ,axis=1,keepdims=True)
    dA_prev = np.dot(W.T,dZ)
    
    return dA_prev, dW, db

def linear_activation_backward(dA, cache, activation):
    linear_cache, activation_cache = cache
    
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db =  linear_backward(dZ, linear_cache)
    
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db =  linear_backward(dZ, linear_cache)    
    
    return dA_prev, dW, db

def L_model_backward(AL, Y, caches):
    grads = {}
    L = len(caches)
    m = AL.shape[1]    
    Y = Y.reshape(AL.shape)
    
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))    
    
    # Lth layer (SIGMOID -> LINEAR) gradients.
    current_cache = caches[L-1]
    dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL, current_cache, activation="sigmoid")
    grads["dA" + str(L-1)] = dA_prev_temp
    grads["dW" + str(L)] =  dW_temp
    grads["db" + str(L)] = db_temp
    
    # Loop from l=L-2 to l=0
    for l in reversed(range(L-1)):
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dA_prev_temp, current_cache, activation="relu")
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp    
    
    return grads

2.5 更新参数

用梯度下降进行参数更新：
$W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}$
$b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]}$

其中， $\alpha$ 是学习率。

def update_parameters(params, grads, learning_rate):
    parameters = params.copy()
    L = len(parameters) // 2
    
    for l in range(L):
        parameters["W" + str(l+1)] =  parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l + 1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l + 1)]

    return parameters