[WPF] Matrix Transform, 矩阵变换. 最最最基础的原理解释.

关于向量:

1. 向量的基

在计算机科学中, 向量, Vector, 通常这么表示:
$$\left[\begin{array}{c}x\\ y\end{array}\right]$$
向量有两个 “基”, $\overline{i}$, 即 $\overrightarrow{1,0}$, $\overline{j}$, 即 $\overrightarrow{0,1}$

向量可以看作这些基乘以一组数的结果, 即: $\overline{v}=\overline{i}\times a+\overline{j}\times b$, 例如 $[1,3]$, 就是:
$$\overline{i}\times 1+\overline{j}\times 3=[1,0]\times 1+[0,1]\times 3=[1,0]+[0,3]=[1,3]$$

2. 改变向量的基

当改变向量的基时, 由于向量是一组数与基的乘法, 所以向量也会随之变化.

例如我们设定两个基为它们顺时针旋转90°后的结果, 即: $\overline{i}=[0,-1],\overline{j}=[1,0]$, 那么 [1, 3] 就变成了:
$$\overline{i}\times 1+\overline{j}\times 3=[0,-1]\times 1+[1,0]\times 3=[0,-1]+[3,0]=[3,-1]$$
你会发现, 这个向量也随之改变了, 而且恰好是顺时针旋转90°

3. 矩阵的乘法:

在计算机科学中, 向量如此表示:
$$\left[\begin{array}{c}x\\ y\end{array}\right]$$
如果是两个向量, 则是这样, 竖着的, 是一个向量:
$$\left[\begin{array}{cc}{x}_1,& x_2\\ y_1,& y_2\end{array}\right]$$
而, 我们刚刚进行的乘法, 其实也是矩阵乘法, 即:
$$\left[\begin{array}{cc}0,& -1\\ 1,& 0\end{array}\right]\times \left[\begin{array}{c}1\\ 3\end{array}\right]=\left[\begin{array}{c}3\\ -1\end{array}\right]$$

矩阵变换

在 WPF 中, 一个矩阵(Matrix)有以下属性: M11, M12, M21, M22, OffsetX, OffsetY.

其中, M11, M12, M21, M22 表示缩放旋转矩阵:
$$\left[\begin{array}{cc}M11,& M12\\ M21,& M22\end{array}\right]$$
它们的默认值是:
$$\left[\begin{array}{cc}1,& 0\\ 0,& 1\end{array}\right]$$
而进行矩阵变换, 也就是将源图形的每一个点, 与这个矩阵相乘, 最终得到另一些点, 构成一个新的图形.

而与默认的这个矩阵相乘, 形状不会有任何变化.

这个矩阵的 M11 和 M21 值, 可以理解为 $\overline{i}$, M12 和 M22 可以理解为 $\overline{j}$, 之前我们提到, 如果变化这两个基的值, 那么最终向量也会发生变化, 而当我们将刚刚旋转 90° 后的 $\overline{i}$ 和 $\overline{j}$ 拿出来直接代入, 也可以发现, 图形直接旋转了 90°.

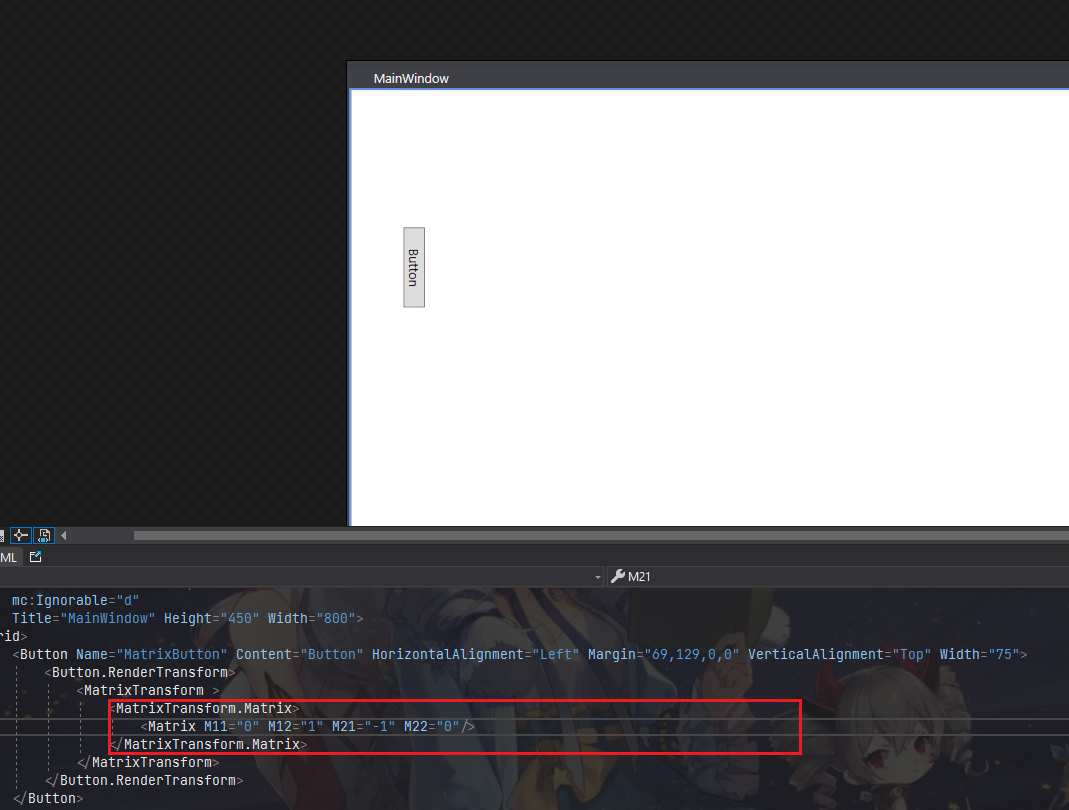
矩阵的基本原理就是矩阵的乘法, 但即便你不理解矩阵的乘法, 去改变 Matrix 中的两个基值, 形状也将跟随基值发生改变.

而 OffsetX 和 OffsetY, 这两个指定了这两个图形的平移, OffsetX 水平偏移量, OffsetY 垂直偏移量.

0. 参考内容:

1. 哔哩哔哩 3Blue1Brown 线性代数
2. 理解矩阵乘法 - 阮一峰的网络日志
3. 矩阵乘法 - endl