完整建模过程+传递函数+框图+仿真源程序+使用说明+指导详见文末


任务概述
双水槽系统是由上下两个水槽串联构成的,来水首先进入上水槽,在上水槽液位有一定高度后借助液位产生的压力通过阀门流入下水槽,通过改变上水槽进水流量来控制下水槽的液位。
本设计综合运用《工业过程控制》课程和其他相关知识,运用机理建模法和测试法(阶跃响应曲线法)建立双水槽对象的数学模型,分析其动静态特性和影响下水槽液位的主要干扰因素并设计出一液位控制方案,实现液位的准确控制,最后进行仿真研究。

设计(研究)内容和要求
1、水箱截面分别为A1和A2,VI和V2的液阻R2、R3为线形液阻,μ1为电动阀门开度(范围是0~100%),kμ为流量比值系数(m3/s),参考教材采用机理法确定H2(S)/μ1(S)通用数学模型。
2、两个水槽动态液位不超过25cm,最大误差不超过±0.2cm,采用静压式压力变送器测量水位,完成变送器选型(量程和精度等),并简述静压式压力变送器安装时的注意事项。
3、通过控制V3和V4阀门,分别测试两个水箱单容特性。设系统稳定一段时间后(上水箱初始液位为13.5cm,下水箱初始液位为2.1cm),进水电动阀门开度阶跃增加10%,并用记录仪同时记录过程输入和输出的变化曲线,经过一段时间后,过程进入新的稳态,试验结束得到的记录曲线就是过程的阶跃响应,分别确定两个水箱的数学模型。
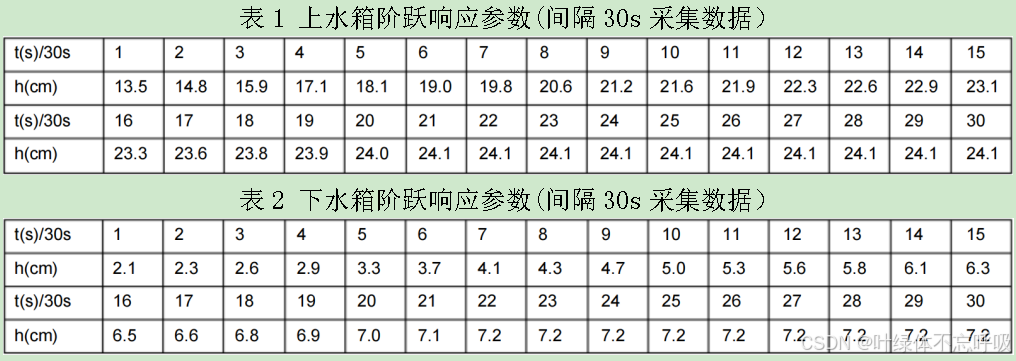
提示:由于实验测定数据可能存在误差,直接使用计算法求解水箱模型会使误差增大。所以使用MATLAB软件对实验数据进行处理,根据最小二乘法原理和实验数据对响应曲线进行最佳拟合后,通过编程绘制拐点切线,再计算水箱模型。
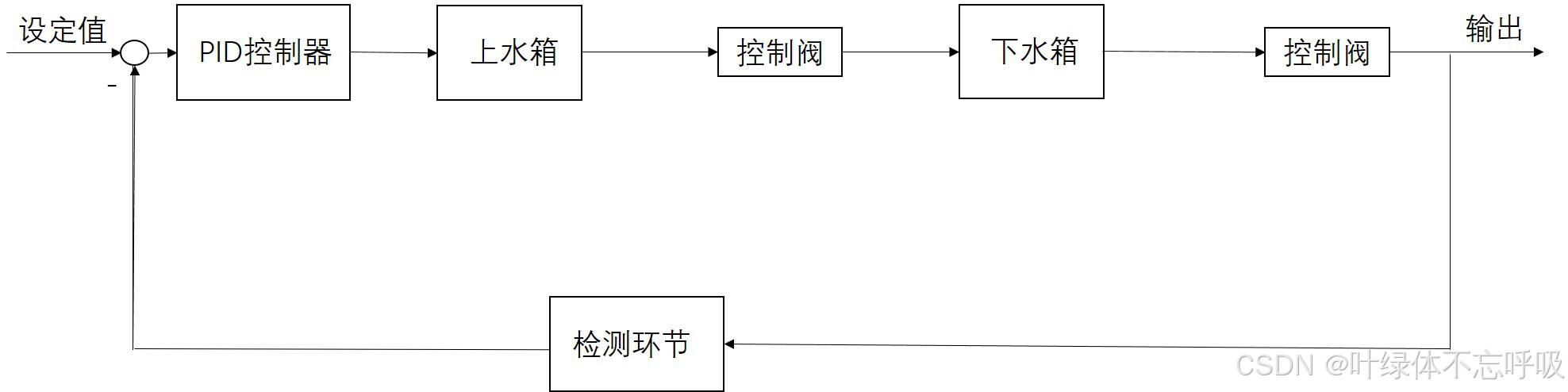
4、为保持下水箱液位的稳定,设计中采用单回路闭环控制系统,将下水箱液位信号经水位检测器送至控制器(PID),控制器将实际水位与设定值相比较,产生输出信号作用于执行器(控制阀),从而改变流量调节水位,设执行机构和检测环节的传递函数为1,用画出系统的框图和仪表流程图。
5、利用MATLAB软件对单回路控制系统进行建模,用4:1衰减曲线法进行PID参数整定,分别采用P、PI、PID调节器,描述整定过程和整定结果,并分析三种调节规律(P、I、D)对控制过程的影响。
6、进水阀阀前压力和流量是主要扰动,为此设计串级控制系统,上水槽为内回路,设计控制方案,画出系统的框图和仪表流程图。
7、利用MATLAB软件对串级控制系统进行建模,用两步整定法进行内外回路参数整定,副回路采用P或PI,主回路采用PI或PID,描述整定过程,结合几个重要的性能指标如:上升时间、峰值时间、调节时间、超调量等分析采用不同调节规律的整定结果(可绘制表格方便对比)。
8、设干扰通道传递函数为一阶惯性环节(参数自己设定),利用MATLAB软件的仿真结果,说明串级控制系统对进入副回路的干扰有较强的抗干扰能力。
机理建模(完整详见文末)

传递函数

//在matlab脚本输入以下程序:
//上水箱用最小二乘拟合曲线:
x=0:30:870;
y=[13.50 14.80 15.90 17.10 18.10 19.00 19.80 20.60 21.20 21.60 21.90 22.30 22.60 22.90 23.10 23.30 23.60 23.80 23.90 24.0 24.1 24.1 24.1 24.1 24.1 24.1 24.1 24.1 24.1 24.1];
p=polyfit(x,y,4);
xi=0:3:870;
yi=polyval(p, xi);
plot(x,y,' b:o', xi,yi,'r');
//得出斜率曲线从而得到初始斜率
dydx=diff(y)./diff(x);
plot(x(1:end-1),dydx);
//绘制带切线的拟合曲线:
y1=0.0433*xi+13.4209;
plot(x,y,' b:o', xi,yi,'r',xi,y1,'--r');>> dydx=diff(y)./diff(x);
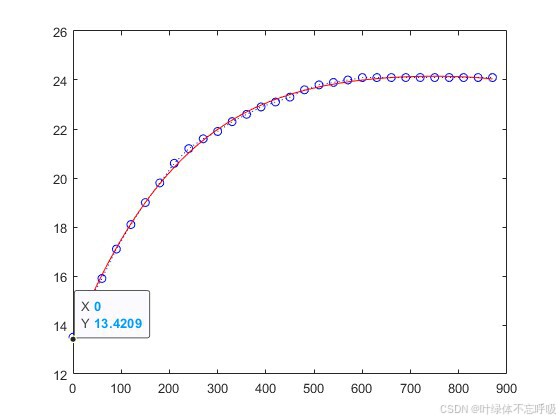
//在matlab脚本输入以下程序:
//下水箱用最小二乘拟合曲线:
x=0:30:870;
y=[2.1 2.3 2.6 2.9 3.3 3.7 4.1 4.3 4.7 5.0 5.3 5.6 5.8 6.1 6.3 6.5 6.6 6.8 6.9 7.0 7.1 7.2 7.2 7.2 7.2 7.2 7.2 7.2 7.2 7.2];
p=polyfit(x,y,4);
xi=0:3:870;
yi=polyval(p, xi);
plot(x,y,' b:o', xi,yi,'r');
//得出斜率曲线从而得到初始斜率
dydx=diff(y)./diff(x);
plot(x(1:end-1),dydx);
//绘制带切线的拟合曲线:
y1=0.0433*xi+13.4209;
plot(x,y,' b:o', xi,yi,'r',xi,y1,'--r');>> dydx=diff(y)./diff(x);
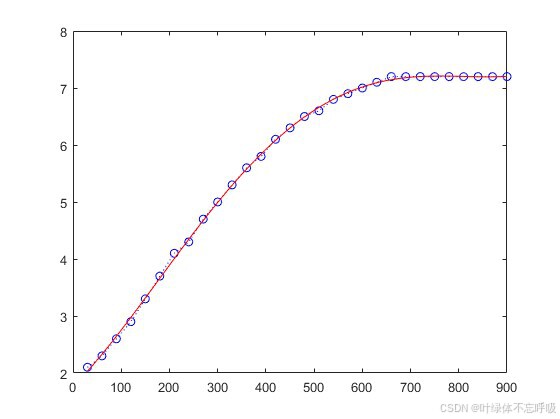
串级控制系统框图
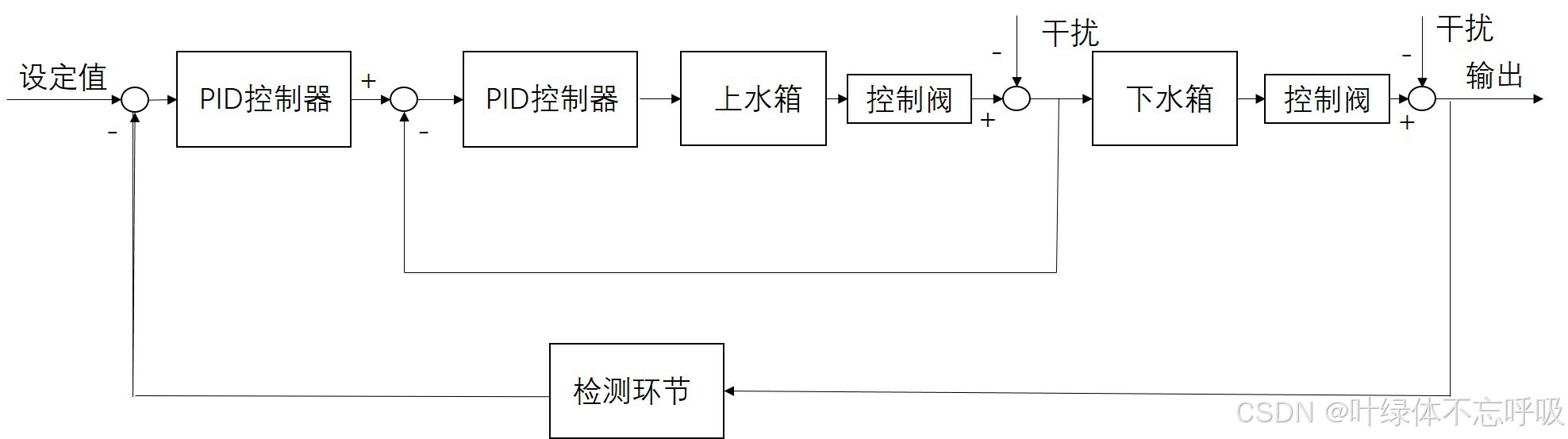
单回路控制系统框图
Matlab\Simulink仿真


仿真结果
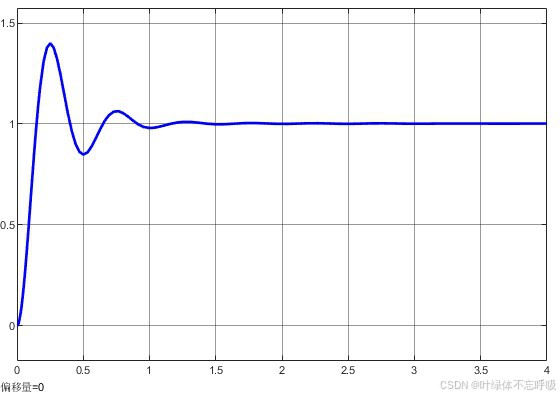
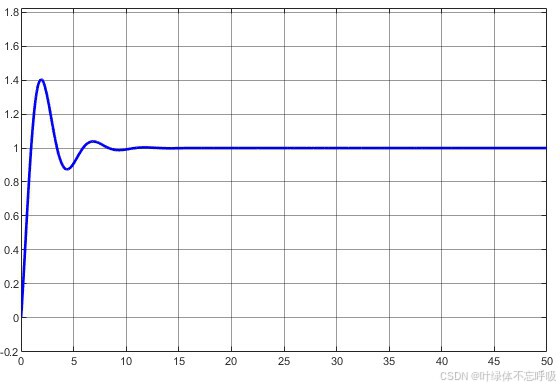

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










