本文提出了一种新的方法，从全景图像的立方体图中估计三维房间布局。通过深度曼哈顿霍夫变换，网络能检测到全局几何模式，尤其是长直线，即使在遮挡情况下也能准确预测。实验表明，这种方法在预测精度和性能上与最新技术相当。
文章目录
摘要
在从单幅全景图像估计三维房间布局的问题中，全局线框图可以简洁地描述房间的重要几何结构。基于这一观察，本文提出一种替代方法，通过在可学习的Hough变换块中建模长程几何模式来估计3D空间中的墙壁。将图像特征从cubemap tile转换到曼哈顿世界的Hough空间，并直接将特征映射到几何输出。卷积层不仅学习局部的类似梯度的线特征，而且利用全局信息，以简单的网络结构成功地预测被遮挡的墙壁。与大多数之前的工作不同，预测是在每个cubemap tile上单独执行的，然后组装起来以获得布局估计。实验结果表明，该方法在预测精度和性能上与最近的最新技术取得了相当的结果。代码可以在https://github.com/Starrah/DMH-Net上找到。
关键词:全景图像,房间布局估计,整体场景结构
1 介绍
从单幅图像中恢复三维几何形状是计算机视觉中研究最多的课题之一。这个不适定的任务通常是在特定的场景下，基于特定的假设或先验知识来解决的。本文工作的目标是在曼哈顿世界假设下，从单一全景图像重建3D房间布局。
正如[4]中所描述的，人类通过使用几何显著的全局结构以极大的效率和鲁棒性感知3D世界。对于我们的任务，一种表示房间布局的直观方法是使用典型3d房间的线框，由水平面上的线和表示垂直墙壁之间连接点的垂直线组成。尽管使用线框图估计3D房间结构是紧凑和稀疏的，但对于视觉算法来说，在外观线索很少的情况下检测又长又细的线条可能是一个挑战，特别是当线条在杂乱的房间中被严重遮挡时。
现有方法要么将结构估计建模为全景或透视的分割问题[40]，要么将几何元素的估计分解为一系列回归问题[34]。本文工作的动机是利用VR领域紧凑和高效的表示，并为该问题提供另一种视角。引入全景图像的cubemap[12]，在每个cubemap tile中获得适当的视觉线索。为了提高直线描述的鲁棒性，采用了广泛应用于线段检测的Hough变换。它使用两个几何项(偏移量和角度)来参数化直线。由于直线的参数化是全局的，估计不容易受到噪声观测和部分遮挡的影响。
在本任务中，将曼哈顿世界假设引入到霍夫变换中，使表示更加简单。房间的线框有三种类型的线。前两种类型是墙-天花板交线和墙-地板交线，它们位于水平面上，在曼哈顿假设下相互垂直。第三种类型是3D空间中的垂直线，表示墙壁之间的连接点，垂直于前两种类型的直线。通过采取一些预处理步骤将房间与相机坐标系对齐，前两种类型的线总是可以与地板/天花板视图中的x轴或y轴对齐。
对输入图像进行对齐后，我们采用等矩形透视(E2P)变换[12,40]从全景图像中得到立方体图后，可以证明沿相机三维空间中某一坐标轴的直线在立方体图瓦片中要么是水平线，要么是垂直线，要么是经过图像中心的直线。这大大简化了线框线的估计，因为只需要检测具有特定特征的线，从而使网络更加集中，从而学习更好的适合曼哈顿房间布局估计的线检测模型。
本文将曼哈顿世界线先验加入深度神经网络中，依靠霍夫变换克服3D房间线框图缺乏外观特征和遮挡的挑战。将霍夫变换嵌入到可训练的神经网络中，以便将曼哈顿世界线框先验与局部学习的外观相结合。本文的主要贡献可以总结如下：
-
通过深度霍夫变换引入曼哈顿世界假设，以捕捉房间布局的长程几何模式。
-
本文提出一种新的框架，分别估计每个cubemap tile上的布局，对标准CNN是无失真的。
-
直接预测具有明确几何意义的曼哈顿线，与最近的最先进工作取得了相当的性能。
2 相关工作
房间布局估计。在过去的十年里，基于单幅图像的三维房间布局估计吸引了大量的研究。以往的研究大多采用曼哈顿世界假设[7]，即所有边界都与全球坐标系对齐。此外，在假设的基础上，利用消失点检测来推断布局。
传统方法提取几何线索,将此任务形式化为一个优化问题。由于图像可能在FoV(view)中不同,从一个角度到360个的全景全景,这些方法因类型的输入图像而变化。在透视图像方面,Delage等。[10]提出一种动态贝叶斯网络模型,以识别室内场景的“墙面”几何图形。李等人。[23]使用定向图(OM),而Hedau等。[16]使用几何上下文(GC)来计算几何推理来解决这个问题。这些策略采用了其他方法,利用增强的评分函数[32,31],或建模objects -布局交互[9,13,46]。
另一方面，由于360度全景图提供了更多的信息，有多篇论文在这个方向上进行了探索。Zhang等[44]提出在全景图像上结合OM和GC来估计布局和3D对象。Yang等[39]以线段和超像素切面为特征，迭代优化3D布局。Xu等人[37]估计布局使用检测到的对象，它们的姿势和场景中的上下文。为了恢复空间布局，Yang等[41]使用了更多的几何线索和语义线索作为输入，而Pintore等[28]使用了梯度图。
基于神经网络的方法具有惊人的能力，可以预先利用数据来改进布局估计。该领域的大多数研究都集中在密集预测上，即训练深度分类网络以像素估计边界概率图[25,30,45]、布局表面类[8,19]或角点热图[22,11]。基于全景图的方法最近引起了人们对三维房间布局估计问题的广泛关注。邹等人[47]直接从单个全景图中预测拐角和边界概率图。Yang等人[40]提出了DuLa-Net，它利用等矩形视图和透视地板/天花板视图图像来生成二维平面图。Pintore等人[27]采用了类似的方法，直接采用等矩形到视角(E2P)转换来推断2D足迹。Fernandez-Labrador等人[11]提出了EquiConvs，一种专门用于等矩形图像的可变形卷积核。Zeng等[43]从单幅室内全景图像中联合学习布局预测和深度估计。Wang等人[36]提出了一种可微深度渲染程序，该程序可以在没有深度地面真值的情况下学习深度估计。尽管对三维房间布局估计进行了广泛的研究，但很少有研究试图产生更紧凑的表示来推断布局。Sun等人提出了HorizonNet[34]和HoHoNet[35]，它们将房间布局编码为边界和角概率向量，并提出从1D预测中恢复3D房间布局。LGT-Net[20]是最近的一项研究，它用水平深度和房间高度表示房间布局。NonCuboidRoom[38]考虑了线条，从透视图像中恢复部分结构，但无法估计整个房间。虽然现有的方法在预测布局方面具有较好的效果，但在表示布局方面仍存在一定的局限性。我们的方法也组装紧凑的结果，但不同于现有的方法。我们的方法不是回归边界值，而是结合了立方体图和线的参数表示。
基于霍夫变换的检测器。Hough等人[18]设计了Hough变换来从图像中检测直线或广义形状[2]，例如圆。传统的直线检测器(如Canny[5]和Sobel[33])通过广泛使用Hough变换，先进行边缘检测滤波，然后在参数空间中识别出显著的峰值。Qi等人。[29]使用Hough投票方案进行3D目标检测。Beltrametti等人在[3]中采用投票的概念进行曲线检测。最近，基于学习的方法证明了Hough变换的表示能力。Han等人。[14]提出Hough变换来聚合直线特征并在参数空间中检测直线。Lin等人考虑通过Hough变换在网络中添加几何直线先验。我们的工作在一个新任务中使用深度Hough特征来解决房间布局估计问题。
3 方法
3.1 概述
我们的目标是估计曼哈顿房间布局从一个单一的360度全景图像。然而，全景图像具有畸变，即三维空间中的直线在全景图像的等矩形视图中可能不是直线。我们不像以往的作品[47,34,36,35]那样直接对全景图像进行预测，而是采用E2P变换[12,40]得到一个包含6个瓦片的立方体图[12]。
给定单个RGB全景图像作为输入，首先我们采取一些预处理步骤来对齐图像，获得立方体图并转换地面真值标签。然后，我们使用我们提出的深曼哈顿霍夫网络(DMH-Net)来检测立方体地图瓷砖上的三种直线。最后，通过基于优化的后处理程序，将线条检测结果进行组装并充分优化，生成三维房间布局。
在第3.2节中，我们将介绍预处理过程。第3.3节介绍了用于房间布局估计的深曼哈顿霍夫变换。我们在第3.4节中总结了所提出的DMH-Net的网络架构。最后，在第3.5节中，我们将介绍基于优化的后处理方法。
3.2 预处理
对齐图像。接收到覆盖360◦H-FoV的单个全景图，我们首先基于LSD算法和[47,34]中提到的消失点对图像进行对齐。我们的方法利用了曼哈顿世界假设和对齐全景的特性。对准后，立方体图瓷砖与三个主轴对齐[7]，即前置摄像头的光轴垂直于墙壁。对齐全景使消失点精确地位于每个立方体贴图的中心。
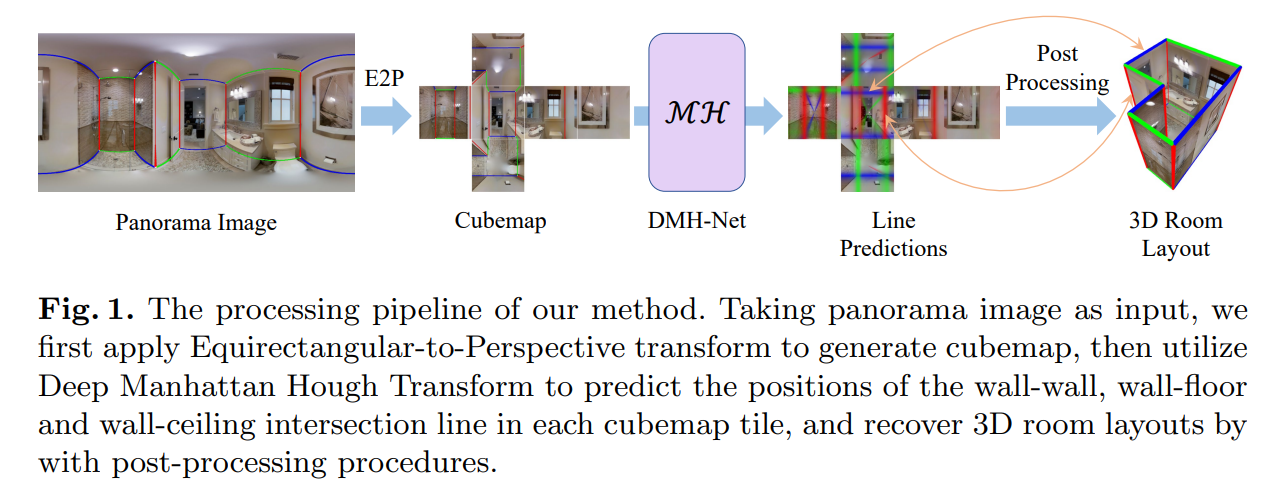
Cubemap的产生。对不同方位角和仰角的等矩形图像进行6次E2P变换，生成 I front , I back , I left , I right , I ceil , I floor I_{\text {front }}, I_{\text {back }}, I_{\text {left }}, I_{\text {right }}, I_{\text {ceil }}, I_{\text {floor }} Ifront ,Iback ,Ileft ,Iright ,Iceil ,Ifloor 等立方体贴图，如图1所示。对于所有的立方体贴图，FoV设置为水平和垂直方向90◦，图像大小设置为512 × 512。
真值转换。对我们使用的所有数据集采用上述对齐方法后，以全景图像中的角点坐标格式提供房间布局的真实值。使用与前面相同的E2P变换，我们还可以将全景图像中的真值角点坐标转换到cubemap中，然后通过原始全景图像中的连接关系将点连接起来，从而得到cubemap中的线。这些线可以分为三种类型:水平线、垂直线和经过图像中心的直线。由于深度曼哈顿霍夫变换只能检测直线而不能检测线段，因此不关心直线的起始点和结束点的具体位置。所以对于一条水平(或垂直)的线，我们只使用y(或x)坐标来表示这条线，而对于一条经过中心点的线，我们只使用方向角θ来表示它。
3.3 曼哈顿深霍夫变换
对于直线检测，传统的Hough Transform[18]用两个参数将图像中的直线参数化为极坐标，一个是方向θ，一个是距离ρ。每个图像像素投票给一个离散参数bin，它表示相应的极坐标。参数空间记为霍夫空间，最大局部峰表示图像中的直线。具体来说，给定单通道输入
X
∈
R
h
0
×
w
0
\mathbf{X} \in \mathbb{R}^{h_{0} \times w_{0}}
X∈Rh0×w0，则霍夫变换H可以表示为:
H
(
ρ
,
θ
)
=
∑
i
∈
l
X
(
x
i
,
y
i
)
(1)
\mathcal{H}(\rho, \theta)=\sum_{i \in l} \mathbf{X}\left(x_{i}, y_{i}\right) \tag{1}
H(ρ,θ)=i∈l∑X(xi,yi)(1)
其中
l
l
l为一条直线，其方向角为
θ
\theta
θ，到坐标原点的距离为
ρ
\rho
ρ,
l
l
l为直线
l
l
l上的每一个点。
我们网络的一个关键概念是检测每个立方体地图瓷砖中房间布局边界的所有可能位置。我们提出将深度网络与霍夫变换相结合用于版图边界检测。具体来说，我们提出了结合深度CNN特征和曼哈顿世界假设的深度曼哈顿霍夫变换(DMHT)。它基于以下两个假设:
- 曼哈顿世界假设，即所有的墙壁、天花板和地板必须相互垂直，并且它们的所有相交线必须平行于某个正交坐标空间(称为曼哈顿空间)的坐标轴之一。
- 输入图像必须对齐，即每个立方体地图瓷砖的相机精确地面向其中一面墙，其光轴平行于曼哈顿空间的坐标轴之一。
在实践中，这两个假设非常简单，因为人类建筑中的大多数房间都遵循曼哈顿世界假设，第二个假设可以通过第3.2节中描述的预处理步骤实现。在这两个假设下，可以证明房间线框图中的任何一条线，包括墙-墙线、墙-天花板线和墙-地板线，要么是立方体瓷砖中的水平线(θ = 0)，要么是垂直线(θ = π/2)，要么是经过立方体瓷砖中心的线(ρ = 0)，这是单点透视的特殊情况17。
如图2所示，给定编码器网络提取的cubemap tile的特征图作为输入，对于特征图的每个通道
X
∈
R
h
×
w
\mathbf{X} \in \mathbb{R}^{h \times w}
X∈Rh×w，深度曼哈顿霍夫变换
M
H
\mathcal{M H}
MH输出三个向量H、V、C，对应于Hough空间中的bins，分别表示水平线、垂直线和经过中心的直线，定义为：
H
(
ρ
)
=
M
H
H
(
ρ
)
=
H
(
ρ
,
0
)
=
∑
x
i
=
−
w
2
w
2
X
(
x
i
,
ρ
)
,
V
(
ρ
)
=
M
H
V
(
ρ
)
=
H
(
ρ
,
π
2
)
=
∑
y
i
=
−
h
2
h
2
X
(
ρ
,
y
i
)
,
C
(
θ
)
=
M
H
C
(
θ
)
=
H
(
0
,
θ
)
=
{
∑
x
i
=
0
w
2
X
(
x
i
,
x
i
⋅
tan
(
θ
)
)
,
∣
tan
(
θ
)
∣
≤
1
∑
y
i
=
0
h
2
X
(
y
i
⋅
cot
(
θ
)
,
y
i
)
,
∣
tan
(
θ
)
∣
>
1
(2)
\begin{aligned} \mathbf{H}(\rho) & =\mathcal{M H}_{H}(\rho)=\mathcal{H}(\rho, 0)=\sum_{x_{i}=-\frac{w}{2}}^{\frac{w}{2}} \mathbf{X}\left(x_{i}, \rho\right), \\ \mathbf{V}(\rho) & =\mathcal{M H}_{V}(\rho)=\mathcal{H}\left(\rho, \frac{\pi}{2}\right)=\sum_{y_{i}=-\frac{h}{2}}^{\frac{h}{2}} \mathbf{X}\left(\rho, y_{i}\right), \\ \mathbf{C}(\theta) & =\mathcal{M H}_{C}(\theta)=\mathcal{H}(0, \theta) \\ & =\left\{\begin{array}{l} \sum_{x_{i}=0}^{\frac{w}{2}} \mathbf{X}\left(x_{i}, x_{i} \cdot \tan (\theta)\right),|\tan (\theta)| \leq 1 \\ \sum_{y_{i}=0}^{\frac{h}{2}} \mathbf{X}\left(y_{i} \cdot \cot (\theta), y_{i}\right),|\tan (\theta)|>1 \end{array}\right. \end{aligned} \tag{2}
H(ρ)V(ρ)C(θ)=MHH(ρ)=H(ρ,0)=xi=−2w∑2wX(xi,ρ),=MHV(ρ)=H(ρ,2π)=yi=−2h∑2hX(ρ,yi),=MHC(θ)=H(0,θ)={∑xi=02wX(xi,xi⋅tan(θ)),∣tan(θ)∣≤1∑yi=02hX(yi⋅cot(θ),yi),∣tan(θ)∣>1(2)
其中
H
\mathbf{H}
H的
ρ
∈
[
−
h
2
,
h
2
]
\rho \in\left[-\frac{h}{2}, \frac{h}{2}\right]
ρ∈[−2h,2h]， V的
ρ
∈
[
−
w
2
,
w
2
]
\rho \in\left[-\frac{w}{2}, \frac{w}{2}\right]
ρ∈[−2w,2w]，
0
≤
θ
≤
2
π
0 \leq \theta \leq 2 \pi
0≤θ≤2π。
H
(
ρ
)
\mathbf{H}(\rho)
H(ρ)是H的箱子，Hough空间参数ρ， V和C也是如此。
为了高效计算所提出的DMHT，有效的离散化是必要的。很自然地，我们可以将ρ离散化为整数，这样H和V中的每个箱子都表示图像中一条1像素宽的线，因此H∈Rh和V∈Rw。在我们的实验中，我们离散θ，使C∈R2(h+w)对于C中的每个箱子，对应的线在坐标为整数的位置与图像边界相交。通过上述离散化技术，DMHT过程可以通过矩阵的加法和乘法实现，具有高度的并行性，适合GPU计算。更多细节请参阅补充材料。
3.4 网络架构
特征提取器。我们采用膨胀残差网络[42,15]作为编码器，利用膨胀卷积提高图像的空间灵敏度，以学习更好的特征进行细线预测。在等矩形视图Iequi中，全景图输入形状为512 × 1024 × 3。对于cubemap的6个贴图中的每个，输入形状都是512 × 512 × 3。为了同时捕获低层和高层特征，提取了编码器网络的中间特征。在下采样层之前，从每个块中收集感知特征。然后，将所有特征输入到5个输入输出大小不同的独立曼哈顿霍夫头中;
曼哈顿霍夫头。如图3所示，Manhattan Hough Head接收cubemap tile的特征图，在Hough空间中生成特征向量进行直线检测。具体来说，给定输入的特征图通道数为c，该模块首先通过2D卷积将特征通道减少到2c，然后通过3.3中描述的DMHT变换得到Hough空间的结果。然后，结果被一个核大小为3的一维卷积层过滤，以捕获某些霍夫箱子周围的上下文信息。该模块的输出是Hough空间中的三个多通道特征向量:H∈Rh× 2c, V∈Rw× 2c, C∈R2(H +w)× 2c。
上采样，融合和生成线预测。由于特征提取器提取的特征图的大小随层的深度而变化，因此五个曼哈顿霍夫头的输出特征向量的大小是不同的。我们将所有的特征向量上采样到相同的大小，即等于原始图像的宽度和高度，h = 512和w = 512，用双线性插值。然后，通过通道级联融合相同类型的特征向量，并通过三个一维卷积层进行滤波。最后，利用Sigmoid函数生成三个单通道1D向量H∈Rh, V∈Rw, C∈R2(H +w)，表示水平线、垂直线和经过图像中心的直线的预测概率。
损失函数。如果我们将概率向量H, V和C的基本真值简单地定义为带有0/1标签的二值向量，那么它将过于稀疏而无法训练，例如，在立方体贴图中512个值中只有不到两个非零值。与HorizonNet[34]类似，我们基于到最近的地面真值线位置的距离的指数函数平滑地面真值。那么，对于H、V、C，我们可以应用二值交叉熵损失:
L
b
c
e
(
X
,
X
∗
)
=
−
∑
i
x
i
∗
log
(
x
i
)
+
(
1
−
x
i
∗
)
log
(
1
−
x
i
)
(3)
\mathcal{L}_{b c e}\left(\mathbf{X}, \mathbf{X}^{*}\right)=-\sum_{i} x_{i}^{*} \log \left(x_{i}\right)+\left(1-x_{i}^{*}\right) \log \left(1-x_{i}\right) \tag{3}
Lbce(X,X∗)=−i∑xi∗log(xi)+(1−xi∗)log(1−xi)(3)
其中
x
i
x_{i}
xi表示
X
\mathbf{X}
X的第i个元素。
布局估计的总损失由三种线路的损耗之和定义:
L
=
L
b
c
e
(
H
,
H
∗
)
+
L
b
c
e
(
V
,
V
∗
)
+
L
b
c
e
(
C
,
C
∗
)
(4)
\mathcal{L}=\mathcal{L}_{b c e}\left(\mathbf{H}, \mathbf{H}^{*}\right)+\mathcal{L}_{b c e}\left(\mathbf{V}, \mathbf{V}^{*}\right)+\mathcal{L}_{b c e}\left(\mathbf{C}, \mathbf{C}^{*}\right) \tag{4}
L=Lbce(H,H∗)+Lbce(V,V∗)+Lbce(C,C∗)(4)
其中符号*表示真值数据。
3.5 后处理
由于我们网络的输出是cubemap上的线存在置信度，因此需要进行后处理以生成最终的3D布局结果。我们的后处理过程包括初始化和优化两个阶段(详见补充资料)。
参数化房间布局表示。在三维空间中，以摄像机为坐标原点，z轴指向天花板，将摄像机到地板的距离设为已知值，类似于邹等人[47]。一个有n面墙的曼哈顿房间的布局可以用n + 1个参数来表示:n代表坐标轴上从摄像机到每面墙的距离，另一个代表房间的高度。
布局参数初始化。给定立方体图中的线预测，我们可以计算出每条墙-天花板和墙-地板相交线的仰角，并且由于相机到地板的距离是已知的，因此可以直接估计到每条墙-地板线的距离，并将其用作布局表示的前n个参数的初始值。虽然摄像机到天花板的距离未知，但通过假设并优化摄像机到天花板和地板的距离之比，使天花板2D帧与地板2D帧具有最高的2DIoU，我们可以得到房间高度的初始估计值。
基于梯度下降的优化。给定初始化的布局参数，我们将其转换为全景图像中的角点坐标，然后转换为立方体地图中的线位置。对于立方体图瓦片中的每条线的位置，我们可以从网络的输出H、V和C中得到线的存在置信度。我们将所有线位置的置信度加在一起，得到一个代表布局参数总体置信度的分数，将损失定义为分数的负值，并使用SGD优化损失，学习率为0.01，无动量，100个优化步骤。通过优化过程，可以有效地将立方体地图上不同瓷砖上的线条预测整合在一起，从全局角度得到更好的布局估计。
4 实验
4.1 实验设置
数据集。我们使用三个不同的数据集。PanoContext数据集[44]和Stanford 2D-3D数据集[1,47]用于cuboid布局估计,而Matterport 3D数据集[6]用于非立方的曼哈顿布局估计。对于公平比较,我们遵循其他工作采用的列车/验证/测试分,[47,348]。
评价指标。我们采用标准的评估指标来估计三维房间布局。对于长方体和非长方体估计，都使用(i) 3D IoU，它被定义为预测和真实值之间联合的体积交集。此外，对于长方体布局估计，还使用(ii)角点误差(CE)和像素误差(PE)，前者是衡量预测角点和真实值之间的平均欧氏距离，后者是像素精度。对于非长方体估计，我们还使用(iv) 2D IoU，它将3D IoU投影到2D平面，以及(v) δ i \delta_{i} δi，它被定义为预测和真实值之间的比率不超过1.25的像素的百分比。对于3D IoU、2DIoU和 δ i \delta_{i} δi，越大越好。角点误差和像素误差越小越好。
基线。将之前的工作与长方体和非长方体房间布局估计进行了比较，并评估了定量性能。我们比较的方法包括PanoContext [44]， LayoutNet [47]， CFL [11]， DuLa-Net [40]，HorizonNet [34]， AtlantaNet [27]， HoHoNet[35]和LED-Net[36]。此外，还比较了Zou等人在[48]工作中提出的改进版本Layoutnet-v2、DuLa-Net-v2和HorizonNet+。根据公布的可比结果，与所有这些方法进行了比较。其中，DuLa-Net[40]和CFL[11]以256 × 512分辨率的图像作为输入，而其他算法的输入分辨率为512 × 1024。此外，PanoContext[44]和LayoutNet[47]除了单一的RGB全景图像外，还需要额外的输入(即线段或方向图)。
实现细节。该网络在PyTorch中实现，并使用Adam[21]进行优化。该网络训练了75个epoch, batch大小为8，学习率为1e-4。该模型在单个NVIDIA A100 GPU上进行训练。对于长方体和非长方体估计，我们使用Pano Stretch[34]，左右翻转来进行数据增强。此外，对于非长方体估计，还对E2P变换生成的cubemap tiles应用垂直翻转和随机90◦旋转增强。
4.2 长方体房间结果
表1分别给出了PanoContext数据集[44]和Stanford 2D-3D数据集[1,47]的定量对比。表中的空白字段表示相应论文中未报告的指标。可以看出，我们的方法在这两个数据集下，在长方体三维房间布局估计中取得了最先进的结果。PanoContext和Stanford 2D-3D数据集的定性结果如图4所示。
4.3 非长方体房间结果
表2为Matterport 3D数据集的定量对比[6]。表中的空白字段表示相应论文中未报告的指标。可以看出，我们的方法在非长方体三维布局估计中实现了与最先进的方法相比具有竞争力的整体性能。Matterport 3D数据集的定性结果如图4所示。我们提出的结果从不同的方法与地面真理一致。更多定性结果请参见补充材料。
4.4 消融研究
在本节中，我们进行了消融研究，以证明我们方法中主要设计的效果。
选择曼哈顿线类型。我们首先研究了DMHT中三种类型线的必要性。我们分别省略了每一种类型的线检测进行了实验。结果总结于表3。所有类型的线路检测都很重要，因为禁用任何一种都会导致明显的性能损失。其中，水平线检测更为重要，水平线构成了天花板和地板线框，这对后处理过程中的初始化至关重要。
Cubemap和DMHT。然后我们验证立方体图表示和DMHT是否有助于恢复3D房间布局。我们用表4中的另外两种消融变体分析了我们整个管道(即III)的有效性。变体(I)将cubemap中的特征编码为我们的特征，但将DMHT中的解码器替换为类似horizonnet的LSTM[34]。(1)中没有DMHT的显著性能下降表明DMHT在我们整个管道中的必要性。我们还比较了深霍夫特征与经典霍夫变换线探测器，请参阅补充资料了解更多细节。变体(II)直接从全景图像中提取特征，然后应用E2P变换将特征输入到DMHT中。这表明立方体映射表示的有效性，因为等矩形特征的失真会降低性能。(I)、(II)和(III)之间的这些变化证明，性能的提高是由于使用了立方体映射和DMHT。
4.5 模型分析
编码器网络。我们首先研究立方体图表示和dmht是如何与模型无关的。我们选择了四种不同的编码器骨干:ResNet-18、34、50[15]和DRN-38[42]。我们改变了我们的网络和horizonnet[34]基线的主干，然后在panocontext数据集上训练和评估网络。如表5所示，我们的方法不仅对我们使用的drn -38架构有效，而且在数量上也始终优于竞争对手。我们的Res-50甚至略高于DRN，可能是由于更深的层。
对遮挡的鲁棒性。然后我们测试我们的方法如何超越竞争对手w.r.t.的阻塞场景。我们在图5(a)中提供定性比较。如图所示,我们的方法在区域被其他杂波遮挡的区域有更准确的预测结果。我们进一步建立了一个更具挑战性的实验。我们手动添加具有挑战性的噪声贴片,然后在不重新训练的情况下测试网络。如图5(b)所示,我们的原始输出比嘈杂区域的竞争对手更合理。此外,在PanoContext数据集上的定量结果也表明,我们的方法实现了一个84.39的3D IoU,而里网是78.74。
局限性。我们展示了两个例子来分析我们对非立方数据的性能限制。图6(a)表明,我们的方法可能会受到区别两层非常紧密的墙的影响。图6(b)显示“VoteSplitting”的低行信心。短线(左最瓦)的概率峰比长线要小。短的可能没有足够的特征箱投票。这些案例可以通过探索增加瓷砖之间的交互和改进的DMHT版本来改进,这将是我们未来的工作。
5 结论
在本文中，我们介绍了一种利用DMHT从全景图像的立方体图估计三维房间布局的新方法。该方法在立方体图上检测水平线、垂直线和经过图像中心的直线，并通过后处理步骤将直线预测结果结合得到房间布局。可学习的Deep Hough变换使网络能够捕获远程几何图案，并精确检测房间布局线框中的线条。定量和定性结果都表明，我们的方法在预测精度和性能方面取得了更好的长方体房间估计结果，并与最新的最先进的方法在非长方体房间估计方面取得了可比的结果。对于未来的工作，结合完全可微后处理或亚特兰大世界假设是一些实际的探索方向。
扫一扫
3638
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
