根据经纬度计算两点之间的方位角
方位角是两点连线与真北方向的夹角,以正北方向为0°,顺时针旋转,范围0~360°。航向角应当就是航行方向与正北方向的夹角。
Matlab代码实现
参考转载自:https://mp.weixin.qq.com/s/zEzEi-Uf4vb_lQQG6Pr6cw
%函数功能:根据A和B经纬度估算两点的距离和方位角(A → B)。
function [fwdAz,revAz,s]=Calculate_AOA_Distance(lon1,lat1,lon2,lat2)
lon1 = deg2rad(lon1) ;
lat1 = deg2rad(lat1); %A点经纬度
lon2 = deg2rad(lon2);
lat2 = deg2rad(lat2); %B点经纬度
f = 1 / 298.257223563;
a= 6378137.0;
b= 6356752.314245;
L = lon2 - lon1;
tanU1 = (1-f)*tan(lat1); cosU1 = 1 / sqrt((1 + tanU1*tanU1));sinU1 = tanU1 * cosU1;
tanU2 = (1-f)*tan(lat2); cosU2 = 1 / sqrt((1 + tanU2*tanU2));sinU2 = tanU2 * cosU2;
lambda = L;
lambda_ = 0;
iterationLimit = 100;
while (abs(lambda - lambda_) > 1e-12 && iterationLimit>0)
iterationLimit = iterationLimit -1;
sinlambda = sin(lambda);
coslambda = cos(lambda);
sinSq_delta = (cosU2*sinlambda) * (cosU2*sinlambda) + (cosU1*sinU2-sinU1*cosU2* coslambda) * (cosU1*sinU2-sinU1*cosU2* coslambda);
sin_delta = sqrt(sinSq_delta);
if sin_delta==0
return
end
cos_delta = sinU1*sinU2 + cosU1*cosU2*coslambda;
delta = atan2(sin_delta, cos_delta);
sin_alpha = cosU1 * cosU2 * sinlambda / sin_delta;
cosSq_alpha = 1 - sin_alpha*sin_alpha;
cos2_deltaM = cos_delta - 2*sinU1*sinU2/cosSq_alpha;
C = f/16*cosSq_alpha*(4+f*(4-3*cosSq_alpha));
lambda_ = lambda;
lambda = L + (1-C) * f * sin_alpha * (delta + C*sin_delta*(cos2_deltaM+C*cos_delta*(-1+2*cos2_deltaM*cos2_deltaM)));
end
uSq = cosSq_alpha * (a*a - b*b) / (b*b);
A = 1 + uSq/16384*(4096+uSq*(-768+uSq*(320-175*uSq)));
B = uSq/1024 * (256+uSq*(-128+uSq*(74-47*uSq)));
delta_delta = B*sin_delta*(cos2_deltaM+B/4*(cos_delta*(-1+2*cos2_deltaM*cos2_deltaM)-B/6*cos2_deltaM*(-3+4*sin_delta*sin_delta)*(-3+4*cos2_deltaM*cos2_deltaM)));
s = b*A*(delta-delta_delta); %距离m
fwdAz = atan2(cosU2*sinlambda, cosU1*sinU2-sinU1*cosU2*coslambda); %初始方位角
revAz = atan2(cosU1*sinlambda, -sinU1*cosU2+cosU1*sinU2*coslambda); %最终方位角
fwdAz =judge(rad2deg(fwdAz)); %将角度归一化至0-360°内
revAz =judge(rad2deg(revAz)); %将角度归一化至0-360°内
s=s/1000; %距离km
end
JAVA代码实现
以下代码是根据matlab代码改编而来,输入两点的经纬度坐标可直接运行。
import com.aircas.model.point;
import static java.lang.Math.*;
public class getAngle {
public static void main(String[] args) {
double[] a = CalculateBraring(116.37047010, 39.83594606, 116.42088584, 39.87221456);
for (double v : a) {
System.out.println(v);
}
}
public static double judge ( double brng){
if (brng < 0) {
return brng + 360;
} else {
return brng;
}
}
//WGS84坐标系,长轴6378137.000m,短轴6356752.314,扁率1/298.257223563。
public static final double f = 1 / 298.257223563;
public static final double a= 6378137.0;
public static final double b= 6356752.314245;
public static double[] CalculateBraring(double lon1, double lat1, double lon2, double lat2) {
//将经纬度坐标转换为弧度
lon1 = Math.toRadians(lon1);
lat1 = Math.toRadians(lat1);
lon2 = Math.toRadians(lon2);
lat2 = Math.toRadians(lat2);
double L = lon2 - lon1;
double tanU1 = (1 - f) * tan(lat1);
double cosU1 = 1 / sqrt((1 + tanU1 * tanU1));
double sinU1 = tanU1 * cosU1;
double tanU2 = (1 - f) * tan(lat2);
double cosU2 = 1 / sqrt((1 + tanU2 * tanU2));
double sinU2 = tanU2 * cosU2;
double lambda = L;
double lambda_ = 0;
double iterationLimit = 100;
double cosSq_alpha = 0;
double sin_delta = 0;
double cos2_deltaM = 0;
double cos_delta = 0;
double delta = 0;
double sinlambda = 0;
double coslambda = 0;
double s = 0;
while (abs(lambda - lambda_) > 1e-12 && iterationLimit > 0) {
iterationLimit = iterationLimit - 1;
sinlambda = sin(lambda);
coslambda = cos(lambda);
double sinSq_delta = (cosU2 * sinlambda) * (cosU2 * sinlambda) + (cosU1 * sinU2 - sinU1 * cosU2 * coslambda) * (cosU1 * sinU2 - sinU1 * cosU2 * coslambda);
sin_delta = sqrt(sinSq_delta);
if (sin_delta == 0) {
}
cos_delta = sinU1 * sinU2 + cosU1 * cosU2 * coslambda;
delta = atan2(sin_delta, cos_delta);
double sin_alpha = cosU1 * cosU2 * sinlambda / sin_delta;
cosSq_alpha = 1 - sin_alpha * sin_alpha;
cos2_deltaM = cos_delta - 2 * sinU1 * sinU2 / cosSq_alpha;
double C = f / 16 * cosSq_alpha * (4 + f * (4 - 3 * cosSq_alpha));
lambda_ = lambda;
lambda = L + (1 - C) * f * sin_alpha * (delta + C * sin_delta * (cos2_deltaM + C * cos_delta * (-1 + 2 * cos2_deltaM * cos2_deltaM)));
}
double uSq = cosSq_alpha * (a * a - b * b) / (b * b);
double A = 1 + uSq / 16384 * (4096 + uSq * (-768 + uSq * (320 - 175 * uSq)));
double B = uSq / 1024 * (256 + uSq * (-128 + uSq * (74 - 47 * uSq)));
double delta_delta = B * sin_delta * (cos2_deltaM + B / 4 * (cos_delta * (-1 + 2 * cos2_deltaM * cos2_deltaM) - B / 6 * cos2_deltaM * (-3 + 4 * sin_delta * sin_delta) * (-3 + 4 * cos2_deltaM * cos2_deltaM)));
s = b * A * (delta - delta_delta); //距离m
double fwdAz = atan2(cosU2 * sinlambda, cosU1 * sinU2 - sinU1 * cosU2 * coslambda); //初始方位角
double revAz = atan2(cosU1 * sinlambda, -sinU1 * cosU2 + cosU1 * sinU2 * coslambda); //最终方位角
double fwdAz_ = judge(Math.toDegrees(fwdAz)); //将角度归一化至0 - 360°内
double revAz_ = judge(Math.toDegrees(revAz)); //将角度归一化至0 - 360°内
s = s / 1000; //距离km
double[] coordinates = new double[3];
coordinates[0] = fwdAz_;
coordinates[1] = revAz_;
coordinates[2] = s;
return coordinates;
}
}
验证正确性
-
Matlab和Java的计算结果进行对比:
以A点坐标(116.37047010, 39.83594606)、B点坐标(116.42088584, 39.87221456)为例,Java代码运行结果如下所示,AB两点之间的初始方位角为46.957度,最终方位角为46.989度,两点相距5.9016千米。

Matlab代码运行结果如下所示:

由此可见,两种代码的运行结果基本一致。 -
通过在线转换计算器进行验证:(https://www.zaixianjisuan.com/dilicesuan/fangweijiao_juli_haiba10.html):

经过方法1和方法2的比较可得,在线转换计算器的结果与代码运行结果基本一致。
- 通过奥维地球的测算功能进行验证:
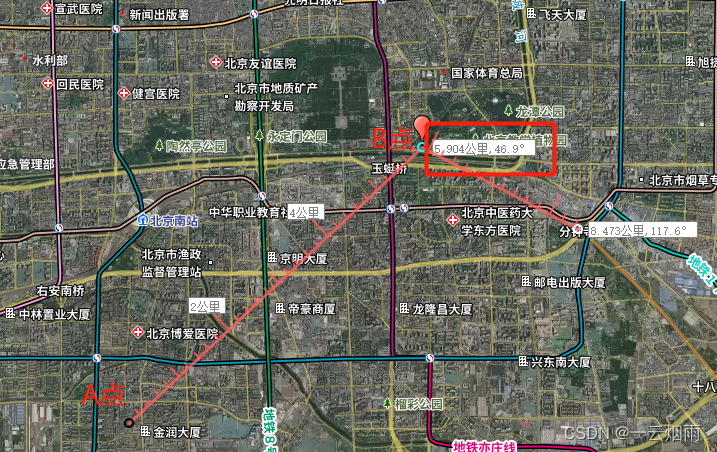







 文章介绍了如何使用Matlab和Java代码计算两点之间的方位角,这两个实现基于经纬度坐标,并通过具体示例进行了验证。Matlab和Java的计算结果在特定坐标下得到的初始和最终方位角以及距离相吻合,证明了代码的正确性。
文章介绍了如何使用Matlab和Java代码计算两点之间的方位角,这两个实现基于经纬度坐标,并通过具体示例进行了验证。Matlab和Java的计算结果在特定坐标下得到的初始和最终方位角以及距离相吻合,证明了代码的正确性。
















 1355
1355

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








