加速度计和陀螺仪——姿态位置求解

~夕上林~

已于 2025-03-06 19:14:52 修改

阅读量4k

点赞数 28

文章标签：算法

于 2024-12-01 03:14:30 首次发布

本文链接：https://blog.csdn.net/m0_49842530/article/details/144094059

版权

1. 案例

背景

使用给定的GITHUB代码和数据，编写主函数以满足要求。（左脚数据正常满足要求，右脚数据无法满足要求；最近也是学习四旋翼飞行器见到了同样的数据类型，所再来深入研究一下）

数据类型

acc_x

acc_y

acc_z

gyr_x

gyr_y

gyr_z

数据来源

①加速度计(ACC)：加速度计是用来测量物体在空间中的加速度，包括由于重力产生的加速度和物体运动产生的加速度。它能够检测物体在X、Y、Z三个轴向上的加速度变化，从而可以计算出物体的速度和位置（通过积分加速度值）。

加速度计简易原理可参考：https://blog.csdn.net/weixin_44702605/article/details/137149974

（其中让我感兴趣的是再保持相对静止不动的情况下，加速度计会显示重力加速度的值 $-g$ ）

②陀螺仪(GYR)：陀螺仪是用来测量物体的角速度，即物体绕X、Y、Z轴的旋转速度。它能够检测物体的动态变化，比如旋转和倾斜，从而可以计算出物体的角度和姿态。

陀螺仪简易原理可参考：一文读懂系列 —— 陀螺仪 - 知乎秒懂！陀螺仪的工作原理！ - 知乎

坐标系

全局坐标系(Global Coordinate System)，又称惯性坐标系
局部坐标系(Body Coordinate System)

一般的全局坐标系表示地球坐标系，局部坐标系为物体本身的坐标系。局部坐标系作用是为了描述物体在全局坐标系中的位置和姿态，另一方面为物体上的点或其他坐标系提供局部的确定位置和姿态标准。

在标准的右手坐标系中，XYZ正方向通常指的是：

X轴：从原点向右的方向。
Y轴：从原点向上的方向。
Z轴：从原点指向观察者的方向（即从屏幕向外的方向）

上边的描述虽然绕口，但是常见的三维笛卡尔坐标系的向上z轴、向右y轴、向前x轴的坐标系也是标准的右手坐标系。具体可以使用 “大拇指朝向x轴、食指朝向y轴、中指朝向z轴”的判断方式，并且右手手指自然弯曲方向为绕x轴旋转的正方向——逆时针方向。同理，“大拇指朝向y轴、食指朝向z轴、中指朝向x轴”“大拇指朝向z轴、食指朝向x轴、中指朝向y轴”也可以判断逆时针为旋转正方向。

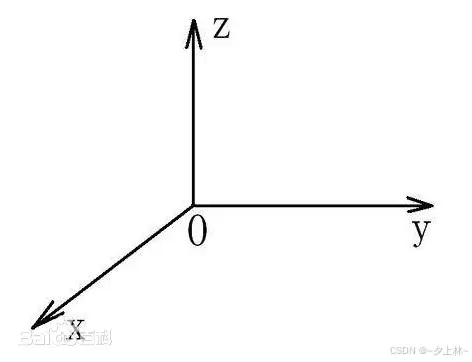
（注：很多的坐标系建立不是依照这个标准右手坐标系建立的，并且旋转的正方向也没有给定，所以之后使用欧拉法时要尤为注意坐标系和旋转正方向！！！）

常见描述两坐标系间关系的方法：

三参数法——欧拉角法
四参数法——四元数法
九参数法——方向余弦法

可参考：四元数、欧拉角和方向余弦的定义及关系_方向余弦欧拉角四元数-CSDN博客

角度

航向角 $\psi$ （Yaw）：是飞行器绕z轴的旋转，也就是飞行器的机头在水平面上的左右偏转。
俯仰角 $\theta$ （Pitch）：是飞行器绕y轴的旋转，也就是飞行器的机头在垂直面上的上下倾斜。
滚转角 $\phi$ （Roll）：是飞行器绕x轴的旋转，也就是飞行器机身的左右翻滚。

具体上述角度的直观图像表示参考：

（虽然在飞行器中 $\psi$ 、 $\theta$ 、 $\phi$ 的物理含义相同，但是参考链接1中的坐标系是标准的右手坐标系，我们使用的是常见直角坐标系，和参考连接2相同）

（根据不同的xyz轴的位置定义，会导致绕轴旋转的角度定义的不同）

数据处理（以四旋翼为例）

可以先观看后文第二节算法部分，以便理解

为什么同时使用加速度计和陀螺仪？

答：单独使用加速度计会存在抖动噪声较大，无法直接使用；单独使用陀螺仪不易受到抖动影响，但测得的数据是角速度，为获取实际姿态需要进行积分，但是长时间的积分行为会导致积分值逐渐偏离实际值。

姿态求解

假设从全局坐标系中转化到局部坐标系的四元数为 $Q=q_0+q_1*\vec{i}+q_2*\vec{j}+q_3*\vec{k}$ ，旋转矩阵为 $C_b^n$ 形式。这里的 $Q$ 时使用陀螺仪数据来获取的，也就是说用陀螺仪数据积分获取当前姿态（即局部坐标系）。更新规则为：四元数微分方程的推导和解算实现 - 知乎

$\frac{dQ}{dt}=\frac{1}{2}Q\otimes \begin{bmatrix}0\\ gyr_x\\gyr_y\\gyr_z \end{bmatrix} =\frac{1}{2} M(gyr)*Q$

$Q(t+T) = Q(t) + T*\frac{dQ}{dt}$

其中 $T$ 为采样时间间隔

加速度计获取的数据是局部坐标系下的加速度数据acc_x、acc_y、acc_z，所以需要将该加速度数据转化到全局坐标系下。

首先进行加速度数据归一化

$\begin{aligned} & acc = \sqrt{acc_x^2 + acc_y^2 + acc_z^2} \\ & a_x = \frac{acc_x}{acc}\\ & a_y = \frac{acc_y}{acc}\\ &a_z = \frac{acc_z}{acc} \end{aligned}$