背包问题的抽象形式

0-1背包

抽象 ：有N件物品，每件物品n有价值量v和消耗c(c可以是多维的，比如卡车载物，一件物品既消耗体积又消耗载重)，在不能重复选择的前提下（即物品最多被选择一次），问如何在给定最大消耗限制（比如卡车有最大容量和载重限制）前提下，选择出的物品集合能使最后的价值量总和最大。

首先，给出状态转移方程：

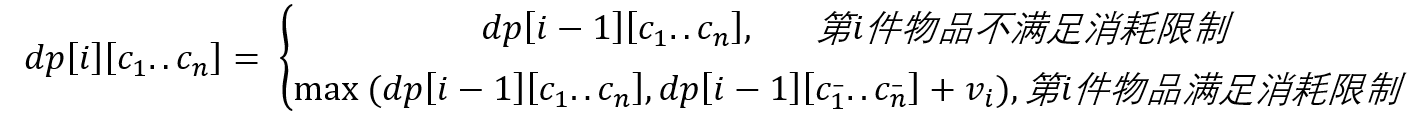
其中，$dp[i][c_1..c_n]$ 表示可选前i件物品的，在最大消耗限制值（比如可以是卡车的体积或者载重的最大值限制值）为$c_1..c_n$下的最优解，$c_1^{-}..c_n^{-}$表示将第i件物品考虑在内后，余下的最大消耗限制值。（比如，某任务原本的容量限制为8，而物品i消耗3的容量，则余下8-3=5的容量限制）

对上面状态方程的解读可以分当前物品能否能小于等于最大消耗限制讨论：
如果大于最大消耗限制，则证明物品i不能被加到最终的物品选择集合中
如果小于等于最大消耗限制，则需要分是加入物品i的收益大还是不考虑物品i的收益大

在动态规划算法中，往往还要思考状态方程处于边界的情形，比如在本例子中的dp[i][0]和dp[0][j]均手动设为0作为迭代的初值，这个步骤往往在算法实现中被忽略。但相反，它们十分关键，初值的确定决定了后面迭代结果的正确性！

0-1背包问题的c++示例：

// costs:  物品的消耗向量
// values: 物品的收益向量
// N：     物品的总数
// Capacity：     最大消耗限制
int knapsack(vector<int> costs, vector<int> values, int N, int Capacity) {
	vector<vector<int>> dp(N + 1, vector<int>(Capacity + 1, 0));
	//遍历物品
	for (int i = 1; i <= N; ++i) {
		//这里 -1 是因为c++的数组下标从0开始，而这里为了对其上面的描述，
		//下标的遍历是从1开始的
		int  c = costs[i-1], v = values[i-1];//计算消耗和收益
		
		//遍历最大消耗限制
		for (int j = 1; j <= Capacity; ++j) {
			if (j >= c) {  
				//当前物品满足最大消耗限制
				dp[i][j] = max(dp[i-1][j], dp[i-1][j-c] + v);  
			} else {
				//当前物品不满足最大消耗限制
				dp[i][j] = dp[i-1][j];
			}
		}
	}
	return dp[N][Capacity];
}

在算法实现时，可以省略维度i，从而实现内存空间的节省，此时要沿着维度j逆向更新dp才能模拟出“dp[i-1][j-c]”，详见下面的代码流程

节省内存版

// costs:  物品的消耗向量
// values: 物品的收益向量
// N：     物品的总数
// Capacity：     最大消耗限制
int knapsack(vector<int> costs, vector<int> values, int N, int Capacity) {
	vector<int> dp(Capacity + 1, 0);
	//遍历物品
	for (int i = 1; i <= N; ++i) {
		int  c = costs[i-1], v = values[i-1];//计算消耗和收益
		
		//逆向遍历
		//这里利用程序运行的时间差，模拟出带有维度i的情形
		//特别注意这里dp[j-c]没有被提前更新，因此能用于递推
		for (int j = Capacity; j >= c; ++j) {
				dp[j] = max(dp[j], dp[j-c] + v);  
		}
	}
	return dp[Capacity];
}

小技巧：当一个迭代更新问题只用到当前态i和过去态i-1时，可以考虑省略这个维度，利用程序运行有先后的特性模拟出维度i的迭代更新，从而达到节省储存空间的目的

完全背包

抽象 ：有N个物品，每个物品n有价值量v和消耗c(c可以是多维的，比如卡车载物，一件物品既消耗体积又消耗载重)，物品能够重复选择，问如何选择物品能使最后的价值量总和最大。

状态转移方程为：

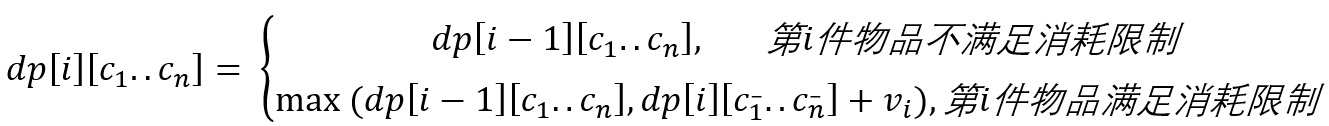
与0-1背包的转移方程类似，只是在物品i满足最大消耗限制时，$dp[i-1][c_1^{-}..c_n^{-}]$替换为$dp[i][c_1^{-}..c_n^{-}]$

完全背包问题的c++示例：

// costs:  物品的消耗向量
// values: 物品的收益向量
// N：     物品的总数
// Capacity：     最大消耗限制
int knapsack(vector<int> costs, vector<int> values, int N, int Capacity) {
	vector<vector<int>> dp(N + 1, vector<int>(Capacity + 1, 0));
	//遍历物品
	for (int i = 1; i <= N; ++i) {
		int  c = costs[i-1], v = values[i-1];//计算消耗和收益
		
		//遍历最大消耗限制
		for (int j = 1; j <= Capacity; ++j) {
			if (j >= c) {  
				//当前物品满足最大消耗限制
				dp[i][j] = max(dp[i-1][j], dp[i][j-c] + v);  
			} else {
				//当前物品不满足最大消耗限制
				dp[i][j] = dp[i-1][j];
			}
		}
	}
	return dp[N][Capacity];
}

同理，在算法实现时，可以省略维度i，从而实现空间压缩，此时要沿j正向更新dp才能模拟出上面带维度i的情况

节省内存版

// costs:  物品的消耗向量
// values: 物品的收益向量
// N：     物品的总数
// Capacity：     最大消耗限制
int knapsack(vector<int> costs, vector<int> values, int N, int Capacity) {
	vector<int> dp(Capacity + 1, 0);
	//遍历物品
	for (int i = 1; i <= N; ++i) {
		int  c = costs[i-1], v = values[i-1];//计算消耗和收益
		
		//正向遍历
		//这里利用程序运行的时间差，模拟出带有维度i的情形
		for (int j = c; j <= Capacity; ++j) {
				dp[j] = max(dp[j], dp[j-c] + v);  
		}
	}
	return dp[Capacity];
}