我们在利用递归解决背包问题时,我们使用了记忆化搜索(详见背包问题的递归形式解),我们其实可以发现在当前参数的递归函数,其返回的值与其拥有临近参数的递归函数的返回值是有关系的。在借鉴了记忆化搜索的思路下,我们其实可以想想,如果要求指定参数的递归函数的返回值,那么如果其临近参数的递归函数的返回值都已经存储在数组中,如dp[][]中,那么我们不需要不断调用递归,直接通过dp数组中的值并通过一定的递推式就能获得所要求的参数的递归函数返回值。这样的话我们就能化递归为动态规划。说白了,动态规划就是利用递推式的形式不断求取最优解。
我们可以根据递归中的关系得到递推式:
然后得到如下的代码:
#include<iostream>
#include<algorithm>
#include<cstdlib>
using namespace std;
#define Max_N 100
#define Max_M 10000
int n;
int sumWeight;
int value[Max_N+1];
int weight[Max_N+1];;
//dp[i][j]用来存放从下标为i的物品开始选出总重不超过j的物品的最大价值
int dp[Max_N+1][Max_M+1];
int main()
{
cin>>n>>sumWeight;
for(int i=0;i<n;i++)
{
cin>>weight[i]>>value[i];
}
//dp[n][j]表示从下标为n开始挑选,可是物品的下标为0~n-1,所以 dp[n][j]=0,这里就类似于原先递归函数中,index>=n时return 0
for(int j=0;j<=sumWeight;j++)
dp[n][j]=0;
//还剩下零重量,装不了任何物品,价值为0
for(int i=0;i<n;i++)
dp[i][0]=0;
for(int i=n-1;i>=0;i--)
{
for(int j=1;j<=sumWeight;j++)
{
if(weight[i]>j) //等效于递归中 weight[index]>leftWeight的情况,当前物品重量大于剩余总重量
dp[i][j]= dp[i+1][j];
else
{
//物品未用完,且当前物品重量小于剩余重量j,此时则分取该品和不取该物品两种情况
dp[i][j]=max(dp[i+1][j],dp[i+1][j-weight[i]]+value[i]);
}
}
}
cout<<"背包问题动态规划1最大物品价值:"<<dp[0][sumWeight]<<endl;
return 0;
}
上面的递推使用大坐标推导小坐标情况,当然我们这里要注意其初始情况,在dp[i][j]中i=n时和j=0时的情况,这在注释中已经解释,这里不做过多的阐述~
当然,递推的公式不是固定,我们还可以使用小坐标推导出大坐标,其递推式如下:
该递推式对应的源代码如下:
#include<iostream>
#include<algorithm>
#include<cstdlib>
using namespace std;
#define Max_N 100
#define Max_M 10000
int n;
int sumWeight;
int value[Max_N+1];
int weight[Max_N+1];;
//dp[i+1][j]用来存放下标从0到i这前i+1个物品开始选出总重不超过j的物品的最大价值
int dp[Max_N+1][Max_M+1];
int main()
{
cin>>n>>sumWeight;
for(int i=0;i<n;i++)
{
cin>>weight[i]>>value[i];
}
//前0个物品,没有物品可选,最大价值为0
for(int j=0;j<=sumWeight;j++)
{
dp[0][j]=0;
}
//重量不超过0,选不了任何物品,价值仍为0;
for(int i=0;i<=n;i++)
{
dp[i][0]=0;
}
for(int i=0;i<n;i++)
for(int j=1;j<=sumWeight;j++)
{
if(weight[i]>j)
{
dp[i+1][j]=dp[i][j];
}
else
{
dp[i+1][j]=max(dp[i][j],dp[i][j-weight[i]]+value[i]);
}
}
cout<<"背包问题动态规划2最大物品价值:"<<dp[n][sumWeight]<<endl;
return 0;
}
同时,要注意初始条件,在dp[i][j]中i=0和j=0时的情况,这里同样在注释中解释过~
在正推和逆推的情况下,我们很容易弄错循环时的变量的变化方向。但是其实是很简单的,如果是大坐标推到小坐标,例如第一个程序,由dp[i+1][j],dp[i+1][j-w[i]]+w[i]中i+1推出i的情况,那么显然i的变化情况是从大变小,也就是从n-1到0(当然这里j是从小坐标推出大坐标,所以j从1~sumWeight是变大的)。
对于变化的范围,我稍微总结下了,比如第一个程序中的dp[i][j],其i的范围是从0~n,而在i=n是初始条件已经被初始化了,所以在循环中只需要将i从n-1变化到0就行。
再举个例子,第二个程序中,dp[i][j]中的i从小坐标推出大坐标,且其范围是0<=i<=n,但是在i=0时已经初始化了,所以i只需要的范围是1~n,但是我们要注意到,在递归式中我们都是以dp[i+1][j]的形式得到当前情况的结果,所以咋循环时i只需要从0变化到n-1就行吗,这样,就能保证i+1最终的变化范围在1~n.
至于程序中其他的坐标范围,同样可以使用这种方式获得变化方向和范围。
但是我小结出的这种方法肯定不是万能的,但是在大多数的动态规划下还是有用的,给大家起到一个借鉴作用吧。











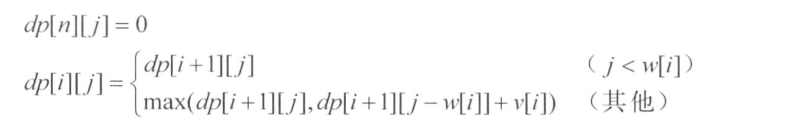















 550
550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








