[论文分享] 深度矩阵分解（Deep Matrix Factorization）综述

最新推荐文章于 2025-04-10 16:58:55 发布

6lyc

最新推荐文章于 2025-04-10 16:58:55 发布

阅读量2.4k

点赞数 19

分类专栏：矩阵分解数据挖掘文章标签：矩阵人工智能机器学习线性代数聚类数据挖掘

本文链接：https://blog.csdn.net/m0_50826544/article/details/136794091

版权

矩阵分解同时被 2 个专栏收录

2 篇文章

订阅专栏

数据挖掘

1 篇文章

订阅专栏

A survey on deep matrix factorizations论文解析

往期推送（持续更新中！）：[ICASSP 2024] CDNMF: 一个可信且高效的社区检测（社区发现，图聚类，Community Detection）方法-CSDN博客

1. 导言

约束低秩矩阵逼近是一种强大的线性降维技术，它能够从大型的数据集中提取相关的关键信息。然而，这种方法由于是线性的以及往往只做了单层映射，难以挖掘出复杂的、多层次的特征。
结合DL的思想，出现了深度矩阵分解（Deep Matrix Factorization, Deep MF）。其结合了矩阵分解的可解释性以及DL的多层次特征提取框架对数据特征进行分层次提取。

每个矩阵 Wi (i=1,...,L) 可以解释为第i层的特征矩阵，每个Hi可以解释为第i层的表示矩阵。总的来说，每分解一次，就使该层的特征的重组出现在下一层中。即对隐藏在数据集中的语义进行多层（深层）解释。

比如，W1对应不同角度的基人脸，W1W2（W1的组合）对应于不同表情的基人脸，W1W2W3（W1W2的组合）对应不同身份的基人脸。

2. Development of Deep MF

2.1 NMF

定义：非负矩阵分解（NMF）即给定一个非负矩阵，将其分解为两个非负矩阵的乘积。其思想是寻找一个新的特征空间，将原数据在该空间进行投影，利用投影结果和空间信息重构原数据。范式如下：

X ≈ W*H （X∈Rmxn,W∈Rmxr,H∈Rrxn>=0）,一般有 r*(m+n)<m*n

数据矩阵：X = [x1,x2,......,xn] ，n个节点表示向量

特征矩阵：W = [w1,w2,...,wr] ，新特征空间的基向量

表示矩阵：H = [hij]，投影结果

则有

xi = h1i * w1 + h2i * w2 + h3i * w3 + ... + hri * wr , i=1,2,...,n （1）

可解释性：由式(1)知，通过非负矩阵分解，每一个节点表示向量都可以投影到新的特征空间并且权重系数hji 表示节点i对第j个特征向量的隶属程度。

求解算法：块坐标下降法（BCD）

把原问题分解为两个子问题

交替优化的两个矩阵之一，同时保持另一个固定：

相比之下：

神经网络通常具有大量的隐藏层和参数，这些参数之间的复杂关系使得整个模型的行为难以理解。这使得难以从模型的结构中直观地理解它是如何进行特征提取和决策的。
神经网络的激活函数通常是非线性的，这意味着模型的输出与输入之间的关系不是简单的线性关系。这种非线性关系使得难以准确地解释模型对输入的响应。
深度学习中使用的优化算法通常是黑盒算法，如随机梯度下降（SGD）等。这些算法使得模型的优化过程不透明，难以理解模型是如何收敛和更新参数的。

2.2 From multilayer MF to deep MF

· multilayer MF：多层MF以顺序方式分解数据矩阵X。在第一层，计算X的低秩因子分解，使得X≈W1H1。在第二层，将矩阵H1分解为H1≈W2H2，以此类推。

然而，多层MF没有继承深度模型的分级学习能力，因为它的分解是纯顺序的。它依次最小化

，没有涉及全局的损失函数。

也就是说，后面层的分解对前面层的分解不产生影响，没有深度模型的反向传播机制。

· deep MF：数据矩阵X仍然经历如多层MF中的连续因子分解，但不是用纯顺序方法，而是通过循环迭代来更新矩阵因子。矩阵因子经历一次顺序更新后利用得到的信息重头迭代更新，实现了反向传播的过程。

2.3 Variants and regularizations of deep MF

（1）Deep orthogonal NMF

· 正交NMF (ONMF) 规定矩阵H是非负的且行正交的，即有：H ≥ 0和HH'=I。容易看出，这两个约束意味着H的每一列最多有一个非零值。因此，每个数据节点只与一个基向量(某一列W)相关，增强了H的稀疏性以及NMF的可解释性。

· Deep model:

对特征矩阵Wi进行分解，可以看出每一层特征矩阵（基向量）是下一层特征矩阵（基向量）的组合。由于H的正交性，也可以解释为每一层特征矩阵（基向量）是上一层特征矩阵（基向量）的组合。即每做一次分解，就得到一个更深层的特征。

H的正交约束：在目标函数中添加一项惩罚项

2）Deep sparse MF

· 稀疏MF的目标是使分解因子更易于解释。特别地，若H的每一列仅包含几个非零项，意味着每个数据节点只与某几个基向量相关。而深度稀疏MF的目标是在每一层都获得稀疏且易于解释的分解因子。通常通过在目标函数添加正则化项或者增加稀疏约束条件来实现。

（3）Deep non-smooth NMF

· Deep nsNMF (dnsNMF)在每一层引入了一个平滑矩阵Sl，促进了每一层分解因子（Wl&Hl）的稀疏性

（4）Deep Archetypal Analysis

· Archetypal Analysis增加了约束

，即表示基向量由数据向量组合而成，继承了原始数据的主要特征，增强了模型的可解释性，使特征矩阵更为直观。（原始数据空间也是重要的特征空间之一）

· Deep model:

（5）Semi-supervised settings

· 为了处理先验信息，在每一层建立一个加权图G，其中节点是数据点，如果两个节点具有相同的标签，则通过一条边连接。如果在第l层，节点X(:，I)和 X(:，j)具有相同的标签,则Gl(i,j)=1。

直觉上来说，当Gl(i，j)=1即X(:，I)和 X(:，j)具有相同的标签，其节点表示Hl(:，j)和Hl(:，k)应该尽可能接近。所以可以在目标函数增加如下正则项，避免X(:，I)和 X(:，j)具有相同的标签时，Hl(:，j)和Hl(:，k)差距过大：

3. Solution of Deep MF

· 初始化：一般对数据矩阵X进行依次顺序分解（多层分解），将得到的矩阵因子作为迭代的初始值。对于每层的Wi和Hi，可以用SVD等分解方式。初始化可以有效减少深度算法的迭代收敛时间。

· 算法求解：与NMF类似，深度MF算法也可以采用块坐标下降法（BCD）求解。

把原问题分解为两个子问题

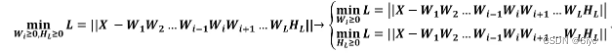
· 超参数的选择：分解层数、每一层特征矩阵的列数（类比PCA）

4. Application of Deep ONMF in Recommender systems

· 考虑一个矩阵 X， X(i，j)表示用户j对电影i的评价，取值在1(非常不喜欢)和10(非常喜欢)之间。在X上应用deep ONMF，并提取出基本用户的层次结构。（用户聚类）

取超参数

则有

W1表示四类基础用户对九部电影的评分，H1表示每个用户作为四类基础用户的比例（概率）。

进一步分解有

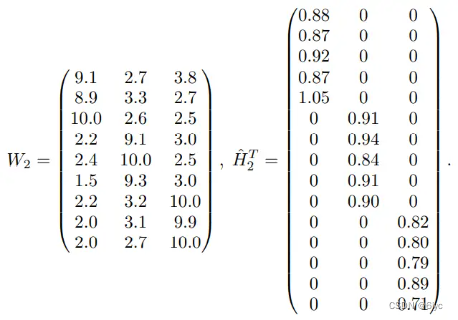
W2表示三类基础用户对九部电影的评分，H2_hat表示每个用户作为三类基础用户的比例（概率）。

可以看出，该模型首先提取4类细化的基本用户，然后在第2层合并了其中两类基本用户，以建模更加全局的用户层次结构。（比如，我们看矩阵X的第6列和第7列，两个用户都对中间三部电影评分高，但第6个用户对前三部电影评分次高，对最后三部电影评分最低，第七个用户恰恰相反。在第一层对这两种用户做了区分，而第二层合并了这两种用户，做了更全局的用户划分。