摘要
最近,多视角聚类(MVC)因为许多现实世界的数据由不同的表示或视图组成而引起了更多关注。关键在于探索互补信息以使聚类问题受益。在本文中,我们提出了一种用于MVC的深度矩阵分解框架,其中采用 半非负矩阵分解 以 逐层学习 多视图数据的层次语义。为了 最大化每个视图的互信息,我们强制要求最终层中每个视图的非负表示相同。此外,为了尊重每个视图数据中的固有几何结构,我们引入了 图正则化项 来耦合深层结构的输出表示。作为一个非平凡的贡献,我们提供了基于 交替最小化策略 的解决方案,并给出了收敛性的理论证明。在三个人脸基准测试上的优越实验结果显示了所提出的深度矩阵分解模型的有效性。
介绍
传统的聚类旨在在单视图数据中识别“相似行为”的群组。由于现实世界的数据通常来自多个来源或由多个不同的特征集表示,最近通过利用异构数据来实现相同目标的MVC得到了广泛研究。不同的特征表征了数据集中的不同信息。例如,一幅图像可以通过颜色、纹理、形状等不同特征来描述。这些多种类型的特征可以从不同的视角提供有用的信息。MVC旨在将多个特征集集成在一起,并揭示不同视图中的一致潜在信息。在开发有效的MVC方法方面进行了大量的研究努力。沿着这条线,Kumar等人开发了共正则化的多视图谱聚类方法,通过共正则化约束同时在不同视图上进行聚类。Gao等人提出在每个视图的子空间表示上同时进行聚类,受到共同的聚类结构指导以保持不同视图之间的一致性
最近,基于非负矩阵分解(NMF)及其变体的MVC研究取得了很多有希望的成果,因为非负性约束使得结果更易于解释。总体思路是通过非负矩阵分解在多视图数据中寻找共同的潜在因子。作为NMF最受欢迎的变体之一,半非负矩阵分解(Semi-NMF)通过将分解的基矩阵放宽到实数值 (实数域 R,包括负数,正数和0) 来扩展NMF。这种做法使得Semi-NMF在现实世界中具有比NMF更广泛的应用。除了首次在MVC应用中探索Semi-NMF之外,我们的方法与现有基于NMF的MVC方法还有另一个区别:我们采用深度结构来进行逐层的Semi-NMF,如图1所示。正如所示,通过深度的Semi-NMF结构,我们逐层地将同一类别的数据样本推向更接近的位置。我们借鉴了深度学习的思想,因此这种做法具有这样的特点。需要注意的是,尽管我们都采用了深度结构,但所提出的方法与现有的基于深度自编码器的MVC方法(Andrew et al)是不同的。一个主要的区别是Andrew et al 基于典型相关分析(CCA),而CCA仅适用于两个视图的情况,而我们的方法没有这样的限制。
总之,在本文中,我们提出了一种通过图正则化的半非负矩阵分解构建深度MVC算法。关键是通过半非负矩阵分解构建深度结构,以寻找具有更一致知识的共同特征表示来促进聚类。据我们所知,这是将半非负矩阵分解应用于深度结构的MVC的首次尝试。我们总结我们的主要贡献如下:
-
通过建立深度的Semi-NMF结构,利用Semi-NMF的强解释性和深度结构的有效特征学习,捕捉隐藏信息。通过这个深度矩阵分解结构,我们逐层解构不重要的因子,并在最终层生成一个有效的共识表示用于MVC。
-
为了尊重数据样本之间的固有几何关系,我们引入了图正则化项来指导每个视图中的共享表示学习。这种做法使得最终层的共识表示保留了跨多个图的大部分共享结构。可以将其视为一种融合方案,以提高最终的MVC性能。
方法
Semi-NMF概述
作为NMF的一种变体,Ding等人将传统NMF的应用从非负输入扩展到了混合符号输入( mix-sign input),同时仍保持了强解释性。其目标函数可以表示为:
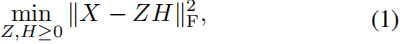
其中, X ∈ R d × n X ∈ R^{d×n} X∈Rd×n 表示具有 n n n 个样本的输入数据,每个样本具有 d d d 维特征。在讨论半非负矩阵分解和K均值聚类等价性的文章中(Ding,Li和Jordan,2010年), Z ∈ R d × K Z ∈ R^{d×K} Z∈Rd×K 可以被视为聚类中心矩阵,而 H ∈ R K × n H ∈ R^{K×n} H∈RK×n, H ≥ 0 H ≥ 0 H≥0 则是潜在空间中的“软”聚类分配矩阵。与传统的NMF类似,紧凑的表示 H H H 通过模拟人脑中的基于部分的表示来揭示隐藏的语义,即心理和生理解释。
然而,在现实中,自然数据可能包含不同的模态(或因素),例如人脸数据集中的表情、光照、姿势等。单一的NMF不足以消除这些不可取因素的影响并提取内在的类别信息。为了解决这个问题,Trigeorgis等人表明,基于半非负矩阵分解的深度模型在数据表示方面具有很好的效果。多层分解过程可以表示为:
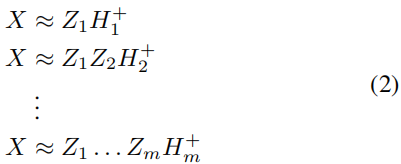
其中,
Z
i
Z_i
Zi 表示第 i 层的基矩阵,
H
i
+
H_i^+
Hi+ 是第
i
i
i 层的表征矩阵。(Trigeorgis 等人,2014年)证明了每个隐藏表征层能够识别不同的属性。受到这项工作的启发,我们提出了一种基于深度矩阵分解技术的多模态学习方法(MVC)。
提出的方法
在MVC设置中,我们将数据样本集表示为 X = { X ( 1 ) , . . . , X ( v ) , . . . , X ( V ) } X = \{X^{(1)},...,X^{(v)},...,X^{(V)}\} X={X(1),...,X(v),...,X(V)}。这里, V V V 表示视图的数量。 X ( v ) ∈ R d v × n X^{(v)} ∈ R^{d_v×n} X(v)∈Rdv×n,其中 d v d_v dv 表示第 v v v 个视图数据的维度, n n n 表示数据样本的数量。然后我们将我们的模型表述为:

在该模型中,
X
(
v
)
X^{(v)}
X(v) 是第
v
v
v 个视图的给定数据。
Z
i
(
v
)
Z_i^{(v)}
Zi(v),
i
∈
{
1
,
2
,
.
.
.
,
m
}
i ∈ \{1, 2,...,m\}
i∈{1,2,...,m} 是第
v
v
v 个视图的第
i
i
i 层映射。
m
m
m 是层数。
H
m
H_m
Hm 是所有视图的共识潜在表示。
α
(
v
)
α^{(v)}
α(v) 是第
v
v
v 个视图的加权系数。
γ
γ
γ 是用于控制权重分布的参数。
L
(
v
)
L^{(v)}
L(v) 是第
v
v
v 个视图的图拉普拉斯矩阵,其中每个图都是以
k
k
k 近邻(k-NN)的方式构建的。视图
v
v
v 的图的权重矩阵是
A
(
v
)
A^{(v)}
A(v),而
L
(
v
)
=
A
(
v
)
−
D
(
v
)
L^{(v)} = A^{(v)}−D^{(v)}
L(v)=A(v)−D(v),其中
D
(
v
)
D^{(v)}
D(v) 是对角线矩阵。
备注1: 由于多视图数据的同质性,第
v
v
v 个视图数据的最终层表示
H
m
(
v
)
H^{(v)}_m
Hm(v) 应该彼此接近。在这里,我们使用共识表示
H
m
H_m
Hm 作为约束,强制多视图数据在多层因子分解后共享相同的表示。
备注2: 构建多个图来约束共同表示学习,以便在最终的聚类中保留每个视图中的几何结构。此外,新颖的图项可以融合多个视图的几何知识,使共同表示更加一致。
优化
为了加速模型中变量的逼近过程,每一层都经过预训练,以获得第 v v v 个视图中第 i i i 层的变量 Z i ( v ) Z_i^{(v)} Zi(v) 和 H i ( v ) H_i^{(v)} Hi(v) 的初始逼近值。预训练的有效性在深度自编码器网络中已经得到证明。与(Trigeorgis等人,2014年)类似,我们将输入数据矩阵 X ( v ) X^{(v)} X(v) 进行分解,近似为 Z 1 ( v ) H 1 ( v ) Z^{(v)}_1 H^{(v)}_1 Z1(v)H1(v),其中 Z 1 ( v ) ∈ R d v × p 1 Z^{(v)}_1 ∈ R^{d_v×p_1} Z1(v)∈Rdv×p1, H 1 ( v ) ∈ R p 1 × n H^{(v)}_1 ∈ R^{p_1×n} H1(v)∈Rp1×n。然后,第 v v v 个视图的特征矩阵 H 1 ( v ) H^{(v)}_1 H1(v) 被分解为 H 1 ( v ) ≈ Z 2 ( v ) H 2 ( v ) H^{(v)}_1 ≈ Z^{(v)}_2 H^{(v)}_2 H1(v)≈Z2(v)H2(v),其中 Z 2 ( v ) ∈ R p 1 × p 2 Z^{(v)}_2 ∈ R^{p_1×p_2} Z2(v)∈Rp1×p2, H 2 ( v ) ∈ R p 2 × n H^{(v)}_2 ∈ R^{p_2×n} H2(v)∈Rp2×n。 p 1 p_1 p1 和 p 2 p_2 p2 分别是第一层和第二层的维度。依此类推,直到预训练完成所有层。随后,通过交替最小化提出的目标函数 Eq. (3) 来微调每一层的权重。首先,我们将代价函数表示为:
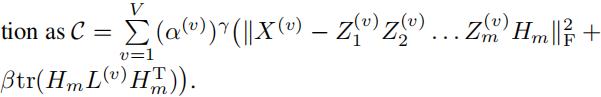
权重矩阵
Z
i
(
v
)
Z^{(v)}_i
Zi(v) 的更新规则。
我们通过固定第
v
v
v 个视图中第
i
i
i 层的其他变量,来最小化关于
Z
i
(
v
)
Z^{(v)}_i
Zi(v) 的目标值。通过设置
∂
C
/
∂
Z
i
(
v
)
=
0
∂C/∂Zi(v) = 0
∂C/∂Zi(v)=0,我们得到以下解:
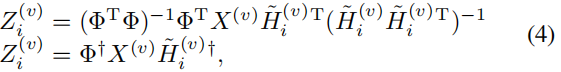
其中,
Φ
=
[
Z
1
(
v
)
.
.
.
Z
i
−
1
(
v
)
]
Φ=[Z^{(v)}_1 ...Z^{(v)}_{i−1}]
Φ=[Z1(v)...Zi−1(v)],
H
~
i
(
v
)
\tilde{H}^{(v)}_i
H~i(v) 表示第
v
v
v 个视图中第
i
i
i 层特征矩阵的重构(或学习到的潜在特征),符号
†
†
† 表示 Moore-Penrose 伪逆。

权重矩阵
H
i
(
v
)
(
i
<
m
)
H^{(v)}_i (i < m)
Hi(v)(i<m) 的更新规则。
根据 (Ding, Li, and Jordan 2010) 的方法,对于
H
i
(
v
)
(
i
<
m
)
H^{(v)}_i (i < m)
Hi(v)(i<m) 的更新规则如下:
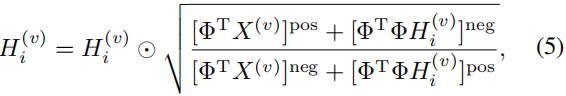
其中,
[
M
]
p
o
s
[M]^{pos}
[M]pos 表示一个矩阵,其中所有负元素被替换为0。类似地,
[
M
]
n
e
g
[M]^{neg}
[M]neg 表示一个矩阵,其中所有正元素被替换为0。也就是说,
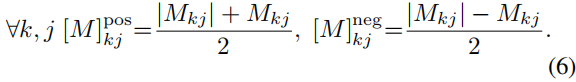
权重矩阵
H
m
H_m
Hm(即
H
i
(
v
)
(
i
=
m
)
H^{(v)}_i (i = m)
Hi(v)(i=m))的更新规则。
由于
H
m
H_m
Hm 包含图项,其更新规则和收敛性性质以前从未被研究过。我们首先给出更新规则,然后证明其收敛性质。
更新规则如下:
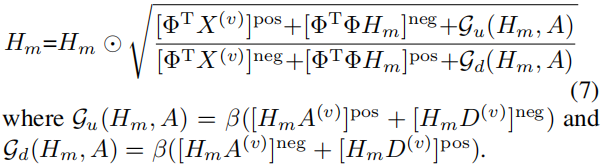
定理1: 更新规则(公式7)的有界解满足KKT条件。
证明:我们引入拉格朗日函数
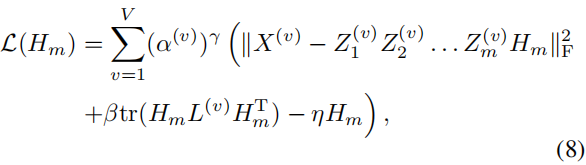
根据拉格朗日乘子
η
η
η 对非负约束
H
m
≥
0
H_m ≥ 0
Hm≥0 的强制条件,拉格朗日函数的零梯度条件为
∂
L
(
H
m
)
/
∂
H
m
=
2
Φ
T
(
Φ
H
m
−
X
(
v
)
)
+
2
H
m
(
D
(
v
)
−
A
(
v
)
)
−
η
=
0
∂L(H_m)/∂H_m = 2Φ^T(ΦH_m − X^{(v)}) + 2H_m(D^{(v)} − A^{(v)}) − η = 0
∂L(Hm)/∂Hm=2ΦT(ΦHm−X(v))+2Hm(D(v)−A(v))−η=0。
同上,把F-范数转换为迹再求导, t r ( ( X − Φ H m ) T ( X − Φ H m ) ) = X T X − 2 X Φ H m + H T Φ T Φ H tr((X-\Phi H_m)^T(X-\Phi H_m)) = X^TX-2X\Phi H_m+H^T\Phi ^T\Phi H tr((X−ΦHm)T(X−ΦHm))=XTX−2XΦHm+HTΦTΦH,利用求导网站对 H m H_m Hm 求导得到 2 Φ T Φ H − 2 Φ T X 2\Phi ^T\Phi H-2\Phi^TX 2ΦTΦH−2ΦTX
根据互补松弛条件,我们可以得到以下结果:
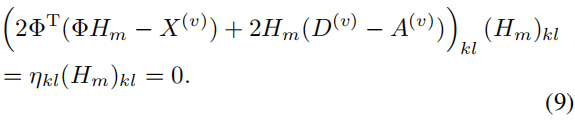
这是一个不动点方程,解在收敛时必须满足该方程。
在公式(7)的收敛解中,满足不动点方程。在收敛时,
H
m
(
∞
)
=
H
m
(
t
+
1
)
=
H
m
(
t
)
=
H
m
H^{(∞)}_m = H^{(t+1)}_m = H^{(t)}_m = H_m
Hm(∞)=Hm(t+1)=Hm(t)=Hm,即
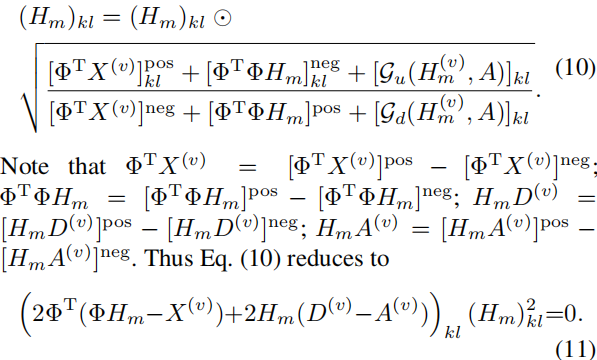
公式(11)与公式(9)是相同的。这两个方程都要求至少有一个因子等于零。两个方程中的第一个因子是相同的。对于第二个因子
(
H
m
)
k
l
(H_m)_{kl}
(Hm)kl 或
(
H
m
2
)
k
l
(H^2_m)_{kl}
(Hm2)kl,如果
(
H
m
)
k
l
=
0
(H_m)_{kl} = 0
(Hm)kl=0,则
(
H
m
2
)
k
l
=
0
(H^2_m)_{kl} = 0
(Hm2)kl=0,反之亦然。因此,如果公式(9)成立,公式(11)也成立,反之亦然。
权重
α
(
v
)
α^{(v)}
α(v) 的更新规则。
类似于 (Cai, Nie, and Huang 2013b),为了方便表示,让我们定义:
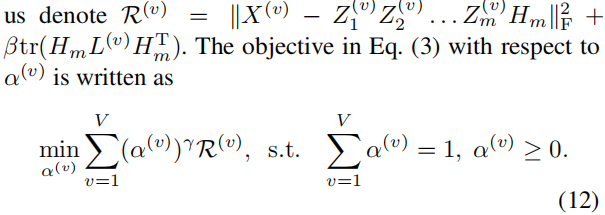
等式的拉格朗日函数(12)已被写成:

其中λ是拉格朗日乘数。通过取等式的导数(13)对于
α
(
v
)
α^{(v)}
α(v) ,并将其设为零,我们得到
幂函数求导:
(
x
a
)
′
=
a
x
a
−
1
(x^a)'=ax^{a-1}
(xa)′=axa−1
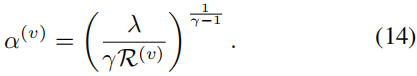
然后我们将公式(14)中的 α ( v ) α^{(v)} α(v) 替换为 ∑ v = 1 V α ( v ) = 1 ∑^V_{v=1} α^{(v)}= 1 ∑v=1Vα(v)=1,并得到以下结果:
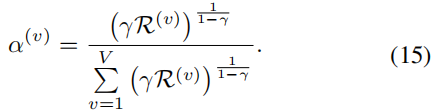
有趣的是,只通过一个参数
γ
γ
γ,我们可以控制不同视图的权重。当
γ
γ
γ 趋近于无穷大时,权重变得相等。当
γ
γ
γ 接近于1时,将最小
R
(
v
)
R^{(v)}
R(v) 值的视图的权重分配为1,其他视图的权重分配为0。
到目前为止,我们已经完成了所有的更新规则。我们迭代地重复这些更新直到收敛。整个算法的概述如算法1所示。在获得优化的 H m H_m Hm 后,可以通过 k-NN 算法在基于 H m H_m Hm 构建的图上执行标准的谱聚类(Ng, Jordan, and Weiss 2001)

Time complexity
我们的深度矩阵分解模型由两个阶段组成,即预训练和微调,因此我们分别对它们进行分析。为了简化分析,我们假设所有层中的维度(即层大小)相同,记为p。所有视图的原始特征维度相同,记为d。V是视图的数量。m是层数。
在预训练阶段,半非负矩阵分解(Semi-NMF)过程和图构建是耗时的部分。复杂度的顺序为
O
(
V
m
t
p
(
d
n
p
+
n
p
2
+
p
d
2
+
p
n
2
+
d
n
2
)
)
O(Vmt_p(dnp + np^2 + pd^2 + pn^2 + dn^2))
O(Vmtp(dnp+np2+pd2+pn2+dn2)),其中
t
p
t_p
tp 是在半非负矩阵分解优化过程中达到收敛所需的迭代次数。通常情况下,
p
<
d
p < d
p<d,因此预训练阶段的计算成本为
T
p
r
e
.
=
O
(
V
m
t
p
(
d
n
p
+
p
d
2
+
d
n
2
)
)
T_{pre.} = O(Vmt_p(dnp + pd^2 + dn^2))
Tpre.=O(Vmtp(dnp+pd2+dn2))。
类似地,在微调阶段,时间复杂度的顺序为
T
f
i
n
e
.
=
O
(
V
m
t
f
(
d
n
p
+
p
d
2
+
p
n
2
)
)
T_{fine.} = O(Vmt_f(dnp + pd^2 + pn^2))
Tfine.=O(Vmtf(dnp+pd2+pn2)),其中
t
f
t_f
tf 是这个微调阶段的迭代次数。总的计算成本为 KaTeX parse error: Expected '}', got 'EOF' at end of input: …e.} + T_{fine.} 。
Experiments
在我们的实验中,我们选择了三个面部图像/视频基准,因为面部包含良好的结构信息,这有助于展示深度NMF结构的优势。以下是数据集和预处理步骤的简要介绍。
Yale数据集 包含了15个主题的165张原始像素图像。每个主题有11张图像,具有不同的条件,例如面部表情、光照、戴/不戴眼镜、照明条件等。Extended Yale B数据集 包含了38个主题的面部图像。每个主题在不同的光照条件和姿势下有64张面部图像。在这项工作中,我们使用了前10个主题的640个图像数据进行实验。Notting-Hill 是一个著名的视频面部基准(Zhang等人,2009年),它来自电影《诺丁山》。其中包括5个主要角色,在76个轨道中有4660个面部。
对于这些数据集,我们遵循了预处理策略(Cao等人,2015年)。首先,将所有图像调整为48×48大小,然后提取三种特征,即强度、LBP(Ahonen,Hadid和Pietik¨ainen,2006年)和Gabor(Feichtinger和Strohmer,1998年)。具体来说,LBP是从裁剪图像生成的9×10像素块的59维直方图。Gabor小波中的尺度参数λ在四个方向θ = {0°,45°,90°,135°}上固定为4,并使用尺寸为25×30像素的裁剪图像。
作为比较基准,我们有以下几种方法:
(1)BestSV对每个视图中的特征执行标准谱聚类(Ng,Jordan和Weiss,2001年)。我们报告最佳性能。
(2)ConcatFea将所有特征连接起来,然后执行标准谱聚类。
(3)ConcatPCA将所有特征连接起来,然后通过PCA将原始特征投影到低维子空间。谱聚类应用于投影的特征表示。
(4)Co-Reg(SPC)(Kumar,Rai和III,2011年)对聚类假设进行共同正则化,以确保来自不同视图的成员资格相互接受。
(5)Co-Training(SPC)(Kumar和III,2011年)借用了协同训练策略的思想,使用其他视图的信息交替修改每个视图的图结构。
(6)MinD(isagreement)(de Sa,2005年)构建一个双分图,该图源自“最小化不一致性”的思想。
(7)MultiNMF(Liu等人,2013年)将NMF应用于将每个视图数据投影到共同潜在子空间。该方法可以粗略地看作是我们提出的方法的单层版本。
(8)NaMSC(Cao等人,2015年)首先对每个视图数据应用(Hu等人,2014年),然后将学习到的表示组合起来,并输入谱聚类。
(9)DiMSC(Cao等人,2015年)通过引入多视图数据表示的互补信息,探究多视图数据的表示之间的多样性。这项工作也是多视图聚类中最新的方法之一。我们不与基于深度自编码器的方法(Andrew等人,2013年;Wang等人,2015年)进行比较,因为这些基于CCA的方法无法充分利用超过2个视图数据,导致不公平的比较。
为了进行全面的评估,我们使用了六个不同的评估指标,包括标准化互信息(NMI)、准确率(ACC)、调整兰德指数(AR)、F分数、精确度和召回率。有关这些指标的详细信息,读者可以参考(Kumar和III,2011年;Cao等人,2015年)。对于所有指标,数值越高表示性能越好。不同的度量方法偏好不同的性质,因此可以从多样的结果中获得全面的视角。对于每个实验,我们重复10次,并报告平均值和标准差。
Result
表1和表2列出了Yale和Extended YaleB数据集上的结果。我们的方法优于所有其他竞争者。对于Yale数据集,我们在NMI上提升了约7.57%、在ACC上提升了5.08%、在AR上提升了8.22%、在F-score上提升了6.56%、在Precision上提升了10.13%、在Recall上提升了4.61%。平均而言,我们将现有的DiMSC方法改进了超过7%。我们的方法之所以取得如此大的改进,可能的原因是Yale和Extended YaleB中的图像数据都包含多个因素,如姿势、表情、光照等。现有的多视角聚类(MVC)方法只涉及一层表示,例如MultiNMF中的一层因子分解,或者NaMSC和DiMSC(Cao等,2015年)中的自表示(系数矩阵Z)。然而,我们提出的方法可以逐层提取有意义的表示。通过深度表示,我们可以消除不良因素的影响,并在最后一层保留核心信息(即类别/标识信息)。
表3列出了Notting-Hill视频数据集的性能。与之前的两个图像数据集相比,这个数据集更具挑战性,因为光照条件变化剧烈且光源是任意的。此外,与Yale和Extended YaleB数据集相反,在Notting-Hill电影中没有固定的表情模式。从表格中可以看出,我们的方法在五个度量指标中取得了优越的结果。唯一的例外是NMI,但我们的性能只比DiMSC差了0.25%。因此,我们可以安全地得出结论,我们提出的方法通常在具有挑战性的Notting-Hill视频数据集上实现了更好的聚类性能。
Analysis
在本小节中,我们评估了所提模型的稳健性和稳定性。首先从目标值和NMI性能的角度研究了收敛性质。然后进行了关于三个关键模型参数β、γ和层大小的分析实验。
收敛性分析。在定理1中,我们从理论上证明了 H m H_m Hm 最复杂的更新满足KKT条件。为了实验上展示整个模型的收敛性质,我们在每次迭代中计算方程(3)的目标值。相应的参数 γ γ γ、 β β β 和层大小分别设置为0.5、0.1和[100, 50]。目标值曲线在图2中以红色绘制。我们观察到目标值稳步下降,然后在大约100次迭代后逐渐收敛。平均NMI(以蓝色表示)在收敛之前有两个阶段:从#1到#14,NMI急剧增加;然后从#15到#30,略微波动,并在收敛点附近达到最佳值。为了安全起见,所有实验的最大迭代次数设置为150次。
参数分析。在所提出的方法中,我们有四组参数,即平衡参数 β β β 和 γ γ γ、层大小 p i p_i pi 以及构建k-NN图时的最近邻数k。选择k-NN图构建算法中的k是一个开放问题(He和Niyogi,2004年)。由于篇幅有限,本文仅包括前三个参数分析实验。然而,我们发现k = 5通常可以取得相对较好的结果。
图3展示了在三种不同层大小设置下,参数 γ γ γ 对NMI结果的影响,即{[100 50],[500 50],[500 200]}。参数 β β β 设置为0.1。 γ γ γ 在网格 { 5 × 1 0 − 3 , 5 × 1 0 − 2 , 5 × 1 0 − 1 , 5 × 1 0 0 , 5 × 1 0 1 , 5 × 1 0 2 } \{5 × 10^{−3},5 × 10^{−2},5 × 10^{−1},5 × 10^0,5 × 10^1,5 × 10^2\} {5×10−3,5×10−2,5×10−1,5×100,5×101,5×102}中进行评估。请注意,为了避免除以0, γ γ γ 不能设置为1。我们观察到,在不同的层大小设置下,当γ = 0.5时,所提出的方法取得最佳效果。一般而言,当 γ γ γ 在 1 0 − 1 、 1 0 − 2 、 1 0 − 3 10^{-1}、10^{-2}、10^{-3} 10−1、10−2、10−3 数量级时,性能相当稳定。我们在实验中将参数γ设置为默认值0.5。
图4探索了模型在参数 β β β 方面的敏感性。考虑到目标函数(3)中两项的可能振幅变化,我们在以下集合 1 0 3 , 1 0 2 , 1 0 1 , 1 0 0 , 1 0 − 1 , 1 0 − 2 , 1 0 − 3 {10^3,10^2,10^1,10^0,10^{-1},10^{-2},10^{-3}} 103,102,101,100,10−1,10−2,10−3 内评估 β β β。可以看出,在三种不同层大小设置下,平均 NMI 结果相对稳定,并且当 β = 1 0 − 2 , 1 0 − 3 β = {10^{-2},10^{-3}} β=10−2,10−3时略微更好。在实践中,我们选择 β = 0.01 β = 0.01 β=0.01 作为默认值。
对于层大小分析,从图3和图4可以看出,[100 50]的设置始终表现最好。根据经验,我们发现最后一层的维度通常比其他层大小更重要(蓝色曲线总是接近红色曲线)。在Yale数据集中,实际的聚类数为10。当将最后一层大小设置为200时,与将最后一层大小设置为50相比,可能引入更多噪声。这可能是为什么绿色曲线(即层大小为[500 200])表现最差的可能原因。
Conclusion
在本文中,我们提出了一种用于MVC问题的深度矩阵分解方法。通过多层半非负矩阵分解,我们的方法能够消除来自不同模态的不良影响,同时只保留输出层中的类别信息。在多个图的引导下,学得的共同表示可以保留每个视图中的几何结构,尤其是共同的结构信息。大量的实验结果通过与九种基准方法的比较验证了所提出的深度矩阵分解结构的有效性。

























 4821
4821











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








