最小公倍数求解完全解读

什么是最小公倍数？

几个数共有的倍数叫做这几个数的公倍数，其中除0以外最小的一个公倍数，叫做这几个数的最小公倍数。

例如 1，2，3 的最小公倍数是 6 。

最小公倍数的适用范围：分数的加减法，中国剩余定理(正确的题在最小公倍数内有解，有唯一的解)。

怎么求最小公倍数？

两种求法：

1. 两数的乘积/最大公约（因）数。
2. S个数的最小公倍数，为这S个数中所含素因子的最高次方之间的乘积。

所以，当我们求的是比较少的数的最小公倍数的时候，可以通过第一种方法来求解，当需要求解大量数据的最小公倍数，那么请用分解质因数的方法！

接下来详细讲解这个分解质因数的方法：

例如：1，求756，4400，19845，9000的最小公倍数？

因756=2*2*3*3*3*7，4400=2*2*2*2*5*5*11，19845=3*3*3*3*5*7*7，9000=2*2*2*3*3*5*5*5，这里有素数2，3，5，7，11．2最高为4次方=16，3最高为4次方=81，5最高为3次方=125，7最高为2次方=49，还有素数11。得最小公倍数为16*81*125*49*11=87318000．

具体例题：选船过河

OJ平台

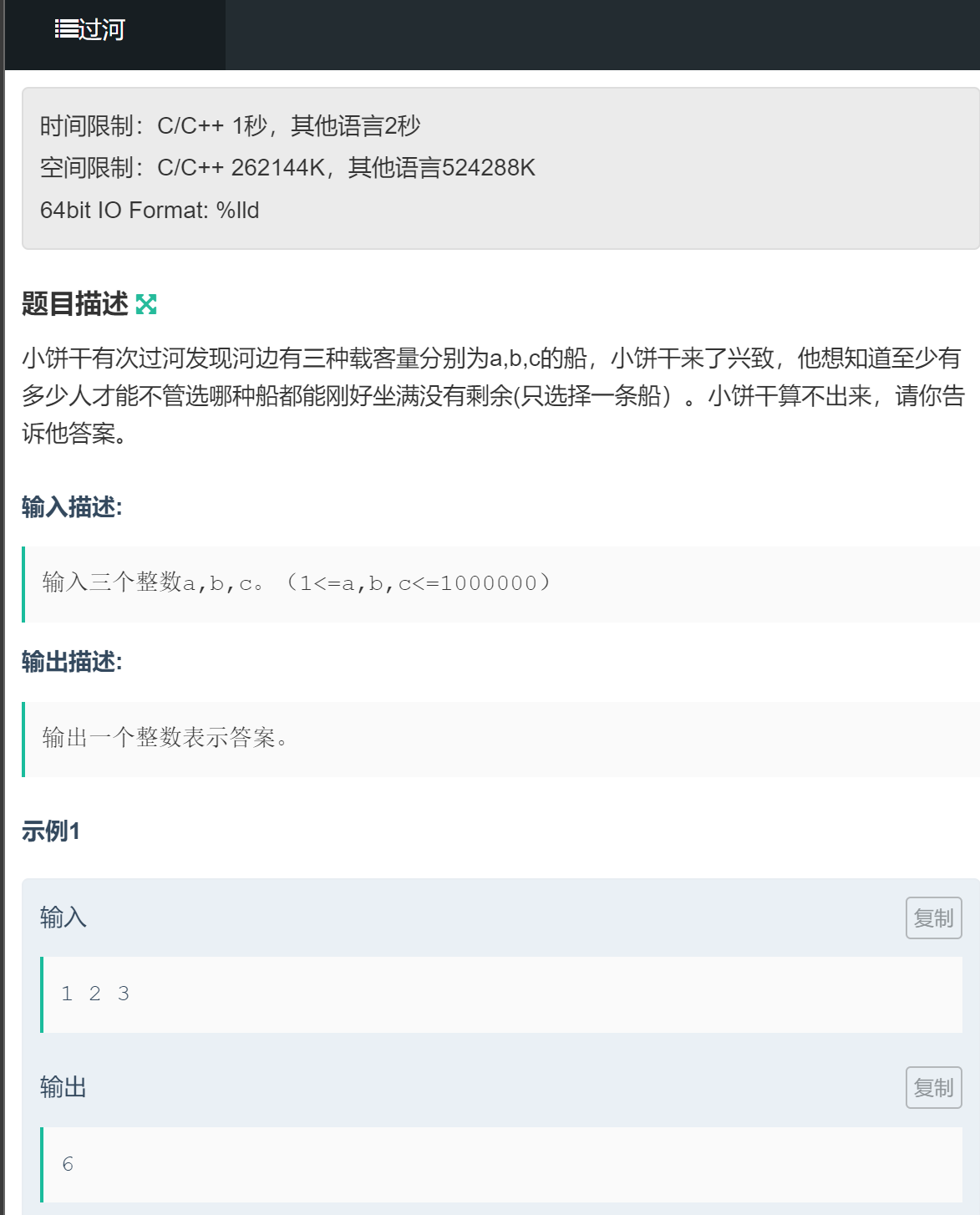
解法一：简单求公因数得到

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int main(){
    ll a,b,c;
    cin>>a>>b>>c;
    ll t = a*b/__gcd(a,b);
    cout<<(ll)t*c/__gcd(t,c);
    return 0;
}

解法二：分解质因数得到

#include<bits/stdc++.h>

using namespace std;
int na[10000000];   //TODO 用于存储某个质因数出现的次数，比如na[i]就是i出现的次数
int nmax = 0, nmin = 0;
using ll = long long;
//TODO 用于把n分解为对应的质因数，然后更新对应质因数的最大出现次数
// 最后只需将所有的质因数以及用对应次数连乘即可得到最小公倍数。
void update(int n) {
    int c = n;
    for (int i = 2; i <= c; i++) {
        int cnt = 0;
        if (n == 1)
            break;
        while (n % i == 0 && n != 1) {
            cnt++;
            n /= i;
        }
        nmax = max(nmax, i);
        nmin = min(nmin, i);
        na[i] = max(na[i], cnt);
    }
}

int main() {
    int a, b, c;
    scanf("%d %d %d", &a, &b, &c);
    update(a);
    update(b);
    update(c);
    ll res = 1;
    //TODO 遍历表格，把质因数以及对应的次数连乘
    for (int i = nmin; i <= nmax; i++) {
        if (na[i])
            res *= (ll) pow(i, na[i]);
    }
    cout << res;
    return 0;
}