7-图神经网络的应用

图机器学习（图神经网络的应用）

1. Graph Augmentation for GNNs

1. 为什么要做图增强

我们在之前都假设原始数据和应用于GNN的计算图一致，但很多情况下原始数据可能不适宜于GNN：

1. 特征层面：输入图可能缺少特征（也可能是特征很难编码）→特征增强

2. 结构层面：

   1. 图可能过度稀疏→导致message passing效率低（边不够嘛）

   2. 图可能过度稠密→导致message passing代价太高（每次做message passing都需要对好几个节点做运算）

   3. 图可能太大→GPU装不下

3. 事实上输入图很难恰好是适宜于GNN（图数据嵌入）的最优计算图

2. 图增强方法

1. 图特征：输入图缺少特征→特征增强
2. 图结构：

​ 1. 图过于稀疏→增加虚拟节点/边

​ 2. 图过于稠密→在message passing时抽样邻居

​ 3. 图太大→在计算嵌入时抽样子图

---

2. 图特征增强Feature Augmentation

1. 应对图上缺少特征的问题（比如只有邻接矩阵），标准方法：

1. constant：给每个节点赋常数特征

​

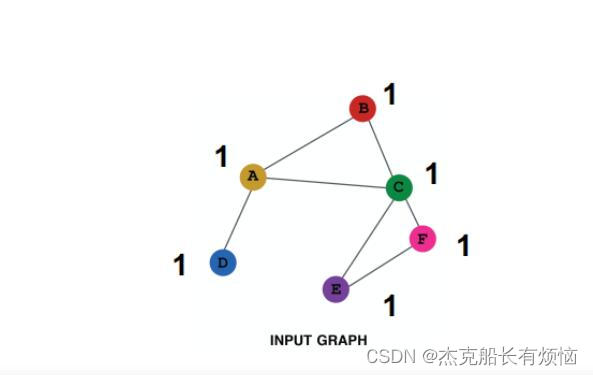
2. one-hot：给每个节点赋唯一ID，将ID转换为独热编码向量的形式（即ID对应索引的元素为1，其他元素都为0）

​

3. 两种方案对比如下表

	constant node feature	one-hot node feature
表示能力	中等：所有节点都一样，但是GNN仍然可以学到图结构信息	高：每个节点ID唯一，所以可以储存节点特有的信息
归纳能力	高：对新节点再赋这个常数就行	低：无法泛化到新节点上，因为对新节点再赋ID的话，GNN无法嵌入这个新ID
计算力代价	低：只有一维特征	高：O(v)维特征，无法应用到大型图上
适用情况	所有图，inductive（归纳）	小图，transductive（直推）

​

2. 有些图结构GNN很难学习到

如

​

两个图中的$v_1$节点度都是2，以$v_1$节点做出来的计算图都是一样的二叉树

​

解决方案是吧cycle count直接作为特征加入到节点信息里面去，采用one hot编码即可

​

另外还可以加入其他的特征：Node degree、 Clustering coefficient、PageRank、 Centrality

---

3. 图结构增强Structure Augmentation

1. 对稀疏图：增加虚拟边virtual nodes或虚拟节点virtual edges

1. 虚拟边：在2-hop邻居之间增加虚拟边

​ 直观上：在GNN计算时不用邻接矩阵A，而用$A+A^2$($A^2$的每个元素是对应节点队之间长度为2的路径数量)

​ 适用范围：bipartite graphs（二部图）

​ 如作者-论文组成的bipartite graph，增加虚拟边可以在合作作者或者同作者论文之间增加链接。这样GNN可以浅一些，训练也会更 快一些（因为在同类节点之间可以直接交互了）但如果添的边太多了也会增加复杂性

​

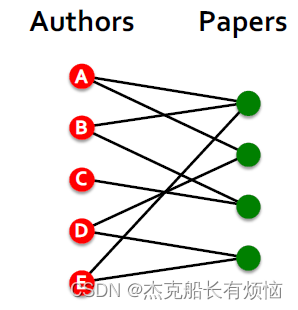
2. 虚拟节点：增加一个虚拟节点，这个虚拟节点与图（或者一个从图中选出的子图）上的所有节点相连这会导致所有节点最长距离变成二（节点A-虚拟节点-节点B）
   优点：稀疏图上消息（message passing）大幅提升

​

2. 对稠密图：节点邻居抽样

在消息传递的过程中，不使用一个节点的全部邻居，而改为抽样一部分邻居。

例如：

先前如：

可能变成：

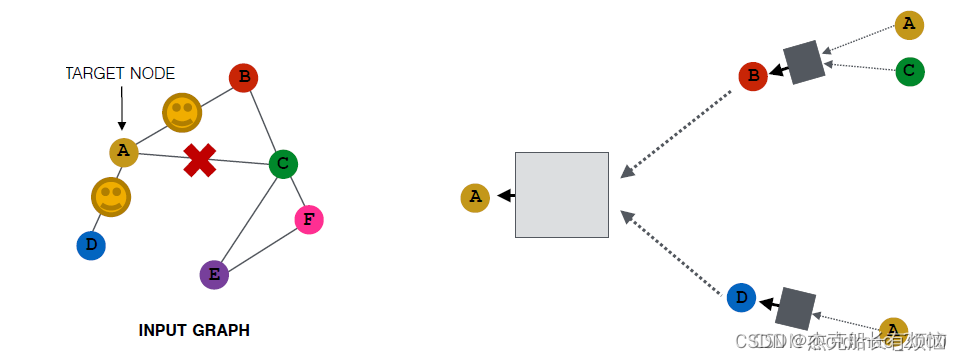
当然，采样是随机的，所有还有可能是：

优点：计算图变小(大大减少运算量)
缺点：可能会损失重要信息（因为有的邻居直接不用了嘛）
当然可以采用抽样不同的邻居来增加模型的鲁棒性

---

4. Prediction with GNNs

1.回顾

到目前为止，我们已经围绕着node embedding展开了一系列的方法的讨论

​

2. Prediction Heads：预测目标向量：k维

这里第一次看到用Head来代表函数，不同粒度下的prediction head：节点级别，边级别，图级别

​

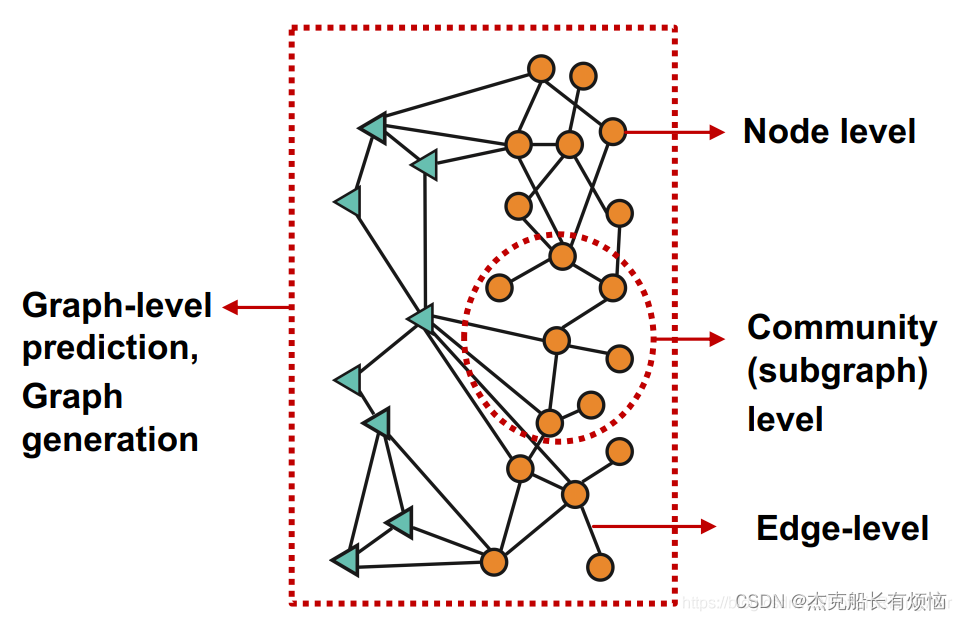
1. 节点级别：直接用节点嵌入做预测

分类任务：在k个类别之间做分类

回归任务：在k个目标上做回归
$$\hat{y}=Hea{d}_{node}{h}_v^L=W^{(H)}{h}_v^{(L)},W^{(H)}\in R^{k\ast d}将d维嵌入映射到k维输出$$

2.边级别：用节点嵌入对来做预测

$$\hat{y}=Hea{d}_{edge}(h_u^{(L)}{h}_v(L))$$

目前常见的有两种方式来处理Head：

1. Concatenation + Linear

​
$$\hat{y}=linear(Concat(h_u^{(L)},h_V^{(L)}))$$

2. 点积

$$\hat{y}=(h_u^{(L)}{)}^T{h}_V^{(L)}$$

​ 这种方法只能应用于1-way prediction（因为点积输出结果就一维嘛），例如链接预测任务（预测边是否存在）。

​ 在应用在k维上：跟GAT中的多头注意力机制类似，多算机组然后合并（公式中的$W^{(1)}，\dots \dots ，W^{(k)}$是可学习的参数）

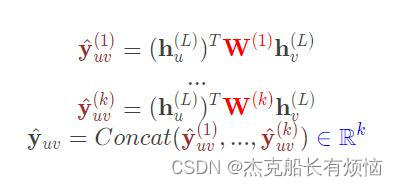
3.图级别：用图中所有节点的嵌入向量来做预测

$$\begin{gathered} \hat{y}=Hea{d}_{graph}(h_v^{(L)}\in {\mathbb{R}}^d,{\forall }_v\in G) \\ Hea{d}_{graph}(.)与单层的GNN中的AGG(.)类似，都是将托干个嵌入聚合为一个嵌入 \end{gathered}$$

1. 这里的head函数和aggregation操作很像，也是有mean、max、sum操作。如果想比较不同大小的图，mean方法可能比较好（因为结果不受节点数量的影响）；如果关心图的大小等信息，sum方法可能比较好。这些方法都在小图上表现很好。但是在大图上的global pooling方法可能会面临丢失信息的问题。

​ 举例：

​ 我们首先采用一维的节点向量$G_1:(-1,-2,0,1,2)、G_2:(-10,-20,0,10,20)$若是用sum做图预测，上面两个图的结果都是0， 但是明显两个图是不一样的。

2. 解决方案：

   将上面所有节点的聚合操作变成分层聚合节点嵌入操作，还是上面的例子我们这回使用$ReLU(Sum(.))$作为head函数。然后分别把前面两个节点和后面三个节点分开做聚合，最后合并得出预测结果。

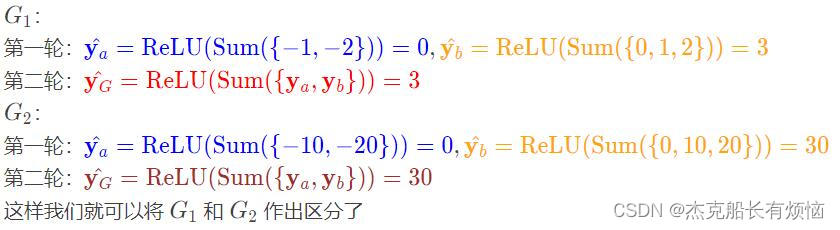
​ 由此可以得到DiffPool算法：

​

​ 1. 每一层都使用2个独立的GNN

​ GNN A：计算节点嵌入‎

​ GNN B：计算节点所属的集群‎

​ A和B在下一层可以并行计算。

​ 2. 对于每个池化层‎

​ 使用来自 GNN B 的聚类分配来聚合由 GNN A‎生成的节点嵌入

​ 为每个聚类创建单个新节点，保证聚类之间的边缘以生成新的池化网络‎

​ ‎联合训练 GNN A 和 GNN B‎

---

5. Predictions & Labels

1.概述

1. 有监督学习supervise learning：直接给出标签（如一个分子图是药的概率）
2. 无监督学习unsupervised learning / self-supervised learning：使用图自身的信号（如链接预测：预测两节点间是否有边）
3. 有时这两种情况下的分别比较模糊，在无监督学习任务中也可能有“有监督任务”，如训练GNN以预测节点clustering coefficient

2. 具体应用情形

	无监督	监督
节点标签	‎节点统计：如聚类系数、PageRank等	‎在引文网络中，节点属于哪个主题区域‎
边标签	‎链接预测：隐藏两个节点之间的边缘，预测是否应该有链接	‎在交易网络中，边缘是否具有欺诈性‎
图标签	图形统计：例如，预测两个图形是否同构‎	在分子图中，图谱的药物相似性‎

​

---

6. Loss Function

1.前置知识

​ 我们用${\hat{y}}^{(i)},y^{(i)}$来统一指代各级别的预测值和标签（$i$是观测编号）

1. 分类任务的标签$y^{(i)}$是离散数值，如节点分类任务的标签是节点属于哪一类。
2. 回归任务的标签$y^{(i)}$是连续数值，如预测分子图是药的概率。
3. 两种任务都能用GNN，其主要区别在于损失函数和评价指标

2. 分类任务的损失函数交叉熵

对于N个样本点，总的loss为：$Loss={\sum }_{i=1}^{N}CE(y^{(i)},{\hat{y}}^{(i)})$

具体计算参考：

3.回归任务的损失函数MSE / L2 loss

MSE的优点：连续、易于微分……等

对于N个样本点，总的loss为：$Loss={\sum }_{i=1}^{N}MSE(y^{(i)},{\hat{y}}^{(i)})$

---

7.评估指标Evaluation Metrics

1. 回归任务

1. root mean square error (RMSE)：$\sqrt{{\sum }_{i=1}^N\frac{(y^{(i)}-\hat{y}(i){)}^2}{N}}$
2. mean absolute error (MAE)：${\sum }_{i=1}^N\frac{|y^{(i)}-\hat{y}(i)|}{N}$

2.分类任务

1. 多分类任务：

   accuracy：$\frac{1}{N}[y^{(i)}=argmax(\hat{y}(i))]$（其中argmax我个人理解的就是找到那个概率最大值对应的索引，看和实际的索引对比，因为实际的值是用one hot向量做的）

2. 二分类任务【1】

​ 1.对分类阈值敏感的评估指标：

​ 1.accuracy（准确率）：如果输出的范围为[0,1]，我们用0.5作为阈值，

​ 2.precision(精确率)/recall(召回率)：因为数据不平衡时可能会出现accuracy虚高的情况。比如99%的样本都是负样本，那么分类 器只要预测所有样本为负就可以获得99%的accuracy，但这没有意义。所以需要其他评估指标来解决这一问题。

​ 2.对分类阈值不敏感的评估指标：ROC AUC（因为这个值本身就是取的是曲线上的一个面积）

【1】二元分类的评估指标：

accuracy（分类正确的观测占所有观测的比例）
precision（预测为正的样本中真的为正（预测正确）的样本所占比例）
recall（真的为正的样本中预测为正（预测正确）的样本所占比例）
F1-Score（precision和recall的调和平均值，信息抽取、文本挖掘等领域常用）

混淆矩阵：

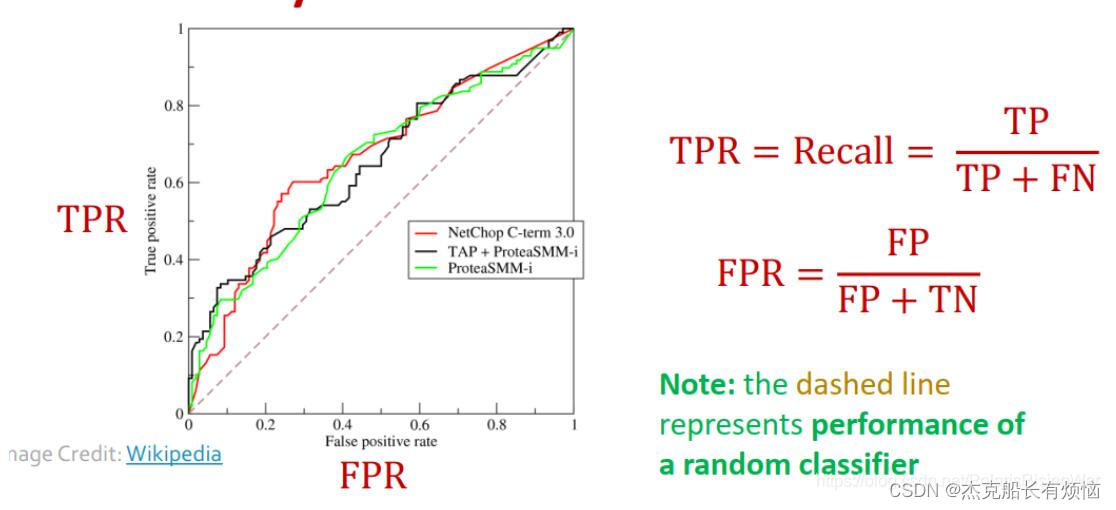
ROC曲线的图示：

AUC，（Area Under Curve），被定义为ROC曲线下的面积，显然这个面积小于1，又因为ROC曲线一般都处于y=x这条直线的上方，所以AUC一般在0.5到1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

AUC的含义为，当随机挑选一个正样本和一个负样本，根据当前的分类器计算得到的score将这个正样本排在负样本前面的概率。

从AUC判断分类器（预测模型）优劣的标准：

• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

---

8.‎拆分数据集-1（方法原理）

主要是数据集的划分，这里的知识点和之前的传统数据集划分有点不一样

1.切分数据集

将数据集切分为训练集、验证集、测试集

​

2. 固定/随机划分

1. ‎固定拆分：我们将拆分数据集一次‎
   ‎ § 训练集：用于优化 GNN 参数‎（权重）
   ‎ § 验证集：开发模型/超参数‎（比如学习率或者是公式中的超参）
   ‎ § 测试集：验证最后模型的性能

2. ‎随机拆分：我们将数据集随机拆分为训练/验证/测试‎
   ‎§ 我们报告不同随机种子的平均性能‎

3. ‎ 问题：对于传统数据集，由于每个样本之间是相互独立的，但是图数据中节点和节点之间是有边相连的，不是相互独立的，因此划分数据集有两种设置。

3. 解决方案：Transductive/Inductive

	Transductive（直推）	Inductive （归纳）
训练集	‎我们使用整个图计算嵌入，并使用节点1和2的标签进行训练‎	‎我们使用节点 1和2 上的图形计算嵌入，并使用节点 1和2 的标签进行训练‎
验证集	‎我们使用整个图计算嵌入，并在节点3和4的标签上进行评估‎	‎在验证时，我们使用节点3和4上的图形计算嵌入，并在节点3和4的标签上进行评估‎
原理	我们将数据集拆分为（训练集、验证集、测试集）保证每个拆分后的数据集都能够观察到全图	‎我们打破分割之间的边缘以获得多个图形‎
图形
应用	点\边	点\边\图
小结	①测试集、验证集、训练集在同一个图上，整个数据集由一张图构成 。 ②全图在所有split中可见。 ③仅适用于节点/边预测任务。	①测试集、验证集、训练集分别在不同图上，整个数据集由多个图构成。 ②每个split只能看到split内的图。成功的模型应该可以泛化到没见过的图上。 ③适用于节点/边/图预测任务。

​

4. 示例

1. 节点分类任务

​ transductive：各split可见全图结构，但只能观察到所属节点的标签

​

​ inductive：切分多个图，如果没有多个图就将一个图切分成3部分、并去除各部分之间连接的边

​

2. 图预测任务

   注意，inductive setting 才能做图分类任务，因为我们的测试集没有看见全图的信息，
   

​

​ 上面看上去一样，但是其实每个数据集给的标签不一样

3. 边预测任务

   这是个 unsupervised / self-supervised 任务，需要自行建立标签、自主切分数据集。需要隐藏一些边，然后让GNN预测边是否存在。

​

​ 这里把保留的边叫：Message edges，去掉的边叫：Supervision edges

​

---

9.拆分数据集-2（具体实施）

1. inductive link prediction split

划分出3个不同的图组成的划分，每个划分集里的边按照第一步分成message edges和supervision edges

​

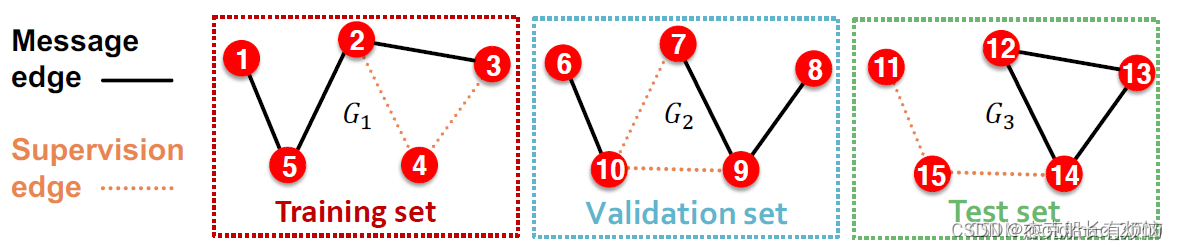
2. Transductive link prediction split

在一张图中进行切分：在训练时要留出验证集/测试集的边，而且注意边既是图结构又是标签，所以还要留出supervision edges

​ 1. 假设我们有一个图的数据集

​

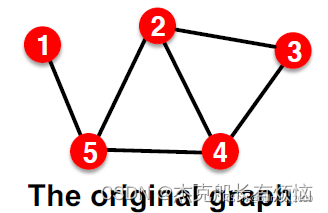
2. 训练：用 training message edges 预测 training supervision edges

​

3. 验证：用 training message edges 和 training supervision edges 预测 validation edges

​

4. 测试：用 training message edges 和 training supervision edges 和 validation edges 预测 test edges

​

5. 链接越来越多，图变得越来越稠密的过程。这是因为在训练过程之后，supervision edges就被GNN获知了，所以在验证时就要应用 supervision edges 来进行 message passing（测试过程逻辑类似）具体来说

阶段	使用的边	预测的边
训练	Training message edges	Training supervision edges
验证	Training message edges + Training supervision edges	Validation edges
测试	Training message edges + Training supervision edges + Validation edges	Test edges

​

​