最近在看有关啁啾的问题,这里对啁啾引起的脉冲展宽和压缩做一下初版的个人理解(可能有点不全,后续若有更好的理解会有更改)。
一、脉冲的形成
首先,先理解一下脉冲的形成,会有助于后续的理解,这里以锁模脉冲为例子:
对于激光腔长为L的激光器,会形成一系列频率间隔为的纵模,每一个纵模在时域内的光场可以写为
,现假设多模激光器的所有振荡模均具有相等的振幅,超过阈值的纵模有(2N+1)个,各相邻模的相位差为
,模频率间隔
,
则第q个振荡模为:
将这2N+1个激光模加起来就是激光输出的总光场:
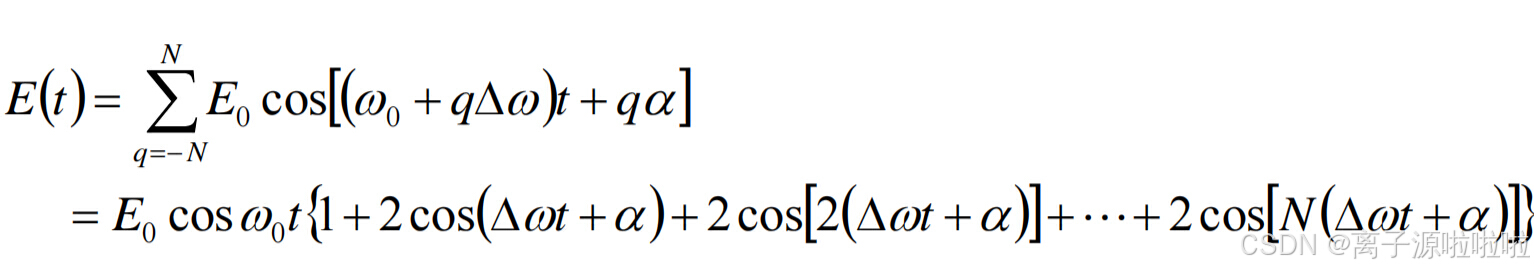
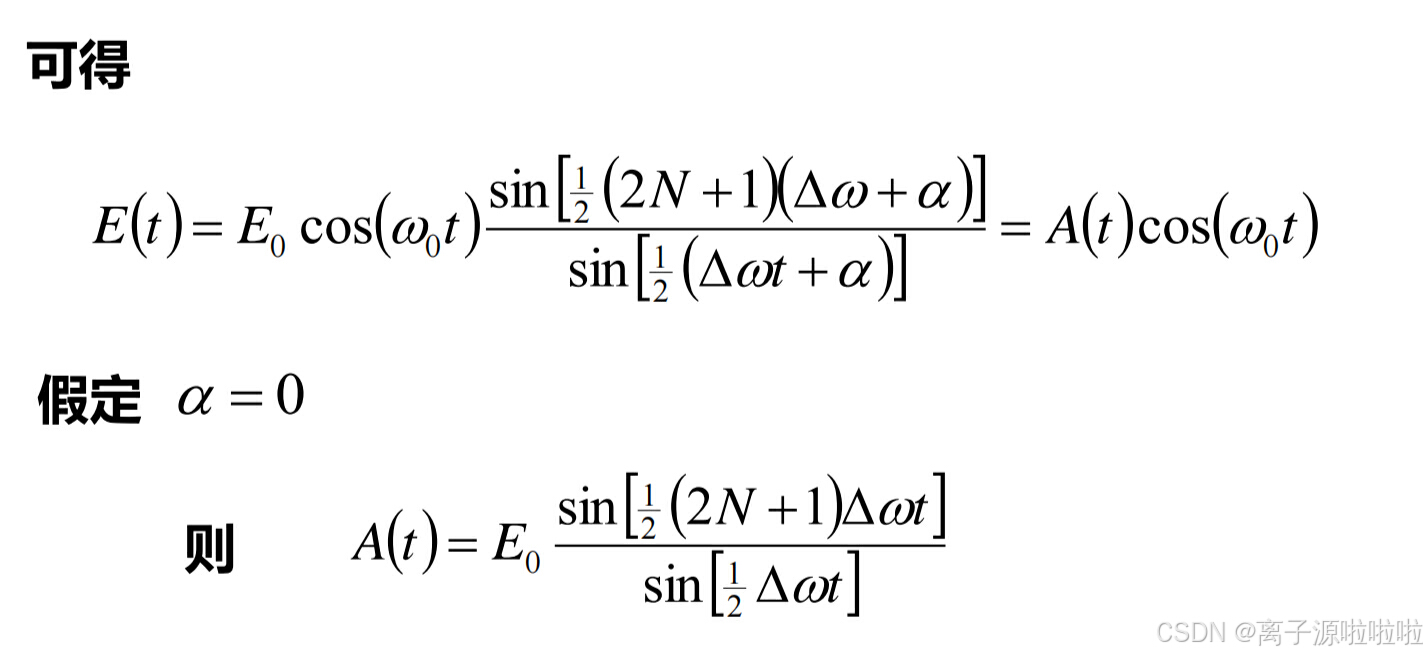
用matlab画出在时域上产生的脉冲:
% 定义常量
E0 = 1; % 假设振幅为1
N = 5; % 假设N为5
delta_omega = 0.1; % 假设频率差为0.1 rad/s
omega_0=20;%中心频率
gain=3;%增益,这里先不考虑
% 创建时间向量
t = linspace(0, 100, 10000); % 从0到100秒,1000个点
% 计算函数值
A_t = E0.* sinc((2*N+1)/2 * delta_omega * t) ./ sinc(delta_omega / 2 * t).* cos(omega_0*t);
% 绘图
figure;
plot(t, A_t);
title('Function Plot of A(t)');
xlabel('Time (s)');
ylabel('Amplitude');
grid on; 
二、正啁啾和负啁啾的定义
啁啾是信号的频率随时间变化的现象,是在时域上对脉冲性质做的一个表征,在一个脉冲周期内各频率成分不是同时到达的,就是激光脉冲的不同频率成分在时域上是不同步的,它分为正啁啾和负啁啾,正啁啾是频率随时间增加,就是激光输出先是低频再是高频,比如一个脉冲上升的前沿是低频,下降的后沿是高频,负啁啾反之。比如正常色散,高频波的折射率大,传播速度慢,而低频波的传播速度快,就形成正啁啾。可见下图所示:
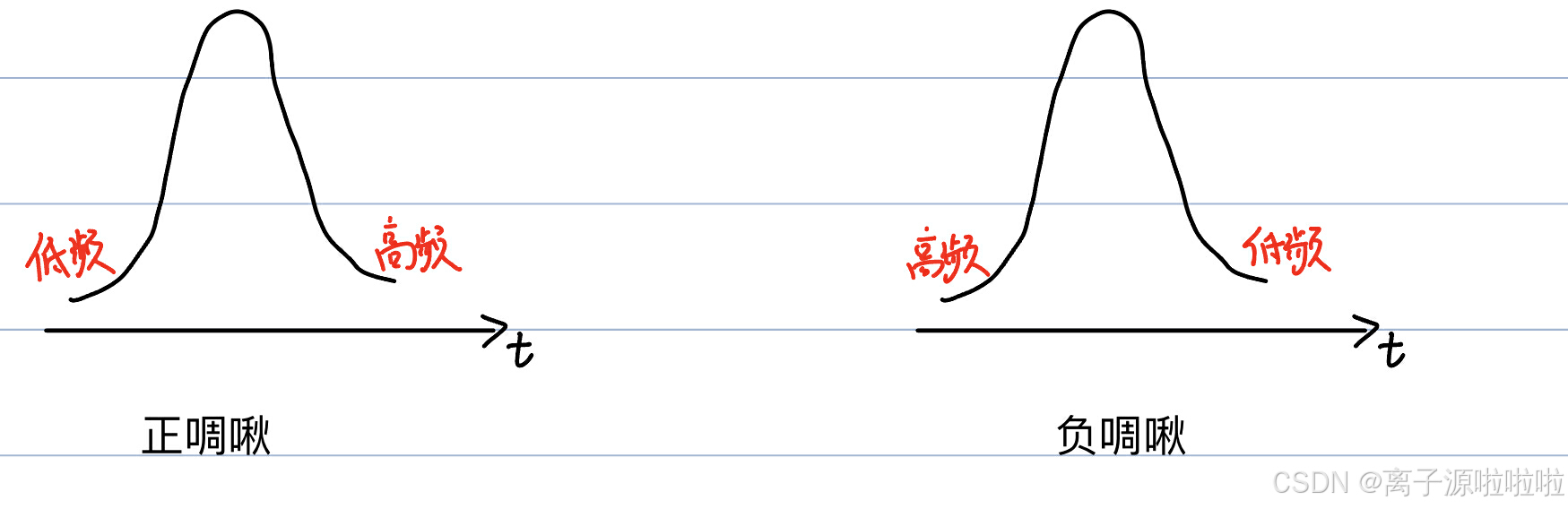
啁啾产生的原因主要是由于介质的折射率由于动态电信号调制的影响产生动态变化,从而引起在介质中传播的光信号的相位发生变化,这种相位的变化直接体现为输出光信号频率的动态变化。
三、色散的啁啾
上述第一节中的锁模脉冲是在不考虑介质的色散条件下生成的,而介质一般都是具有色散的。这里我们从频域角度理解,上述已经提到脉冲是由一系列频率等间隔的模式组成的,也就是说一个脉冲中含有多个不同频率的模式。
这里直接给出群速度色散(GVD)的公式:(可以自行参考光学类教材,应该都会有相关定义的,这里不再阐述)
一般,群速色散定义为群速度对波长
的导数,它与
的关系为:
若先不考虑非线性效应,则光脉冲中某个频率的模式:
其中右式第二项为群速度与相速度的差异,第三项为群速度色散;
正常色散介质
在正色散介质中,频率越低(波长越长)群速度越大。所以脉冲前沿(低频部分)的群速度比后沿(高频部分)的群速度大。因此正常色散介质会引起正啁啾。
反常色散介质
与正常色散介质相反,因此反常色散介质会引起负啁啾。
四、脉冲信号自相位调制(SPM)引起的啁啾
考虑光纤的非线性效应中的自相位调制(SPM)则光脉冲中某个频率的模式应增加自相位调制项:
其中表示光纤中由于光强相关折射率效应产生的影响(具体理论可见非线性光学任意课本的光克尔效应或者自聚焦现象或自相位调制部分):
光强为的光通过长度为L的光纤传输后产生的相移是:
,类似于高斯脉冲,脉冲的不同部位的光强
不同将产生不同的相移,此即自相位调制(SPM)。
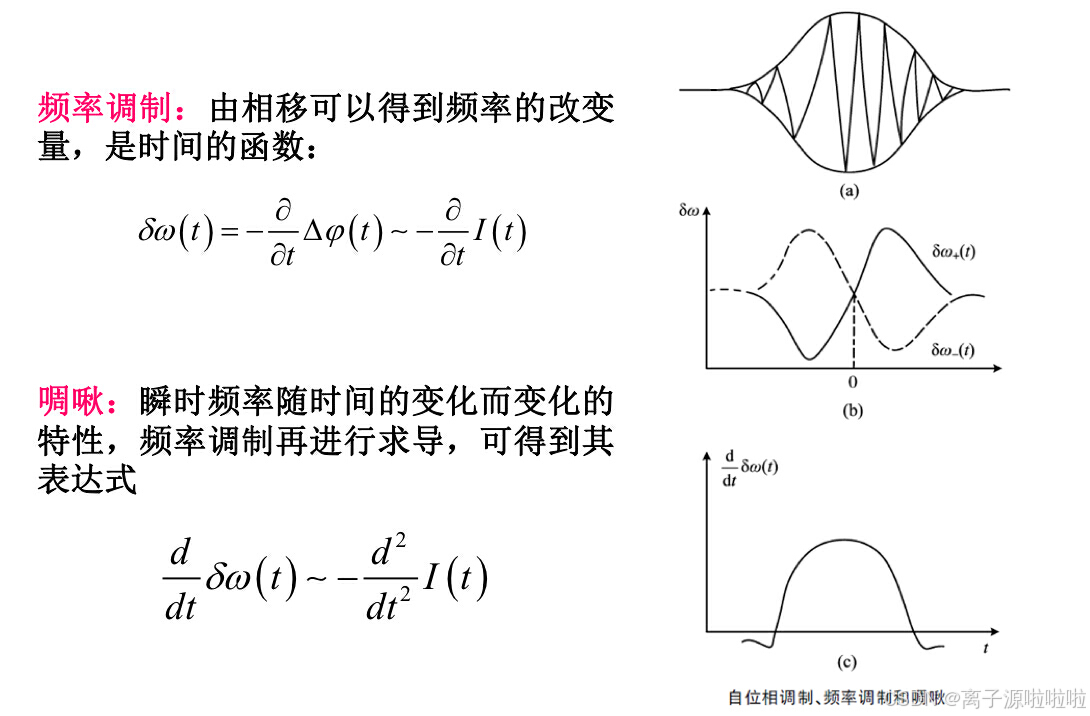
由此可见,对于高斯型正(实线部分)脉冲,脉冲的前后沿为负啁啾,中间沿为正啁啾。
正常色散的介质(形成方波)
1、前沿
前沿为负啁啾,即前沿的前部分为高频率,前沿的后部分为低频率(可以理解为高频率先出现,低频率隔了一段时间才出现);而由于正常色散,低频率的群速度比高频率的快,因此即使低频率后出现,也可以往前追赶高频率,因此导致脉冲的前沿部分被压缩。
2、中间沿
中间沿为正啁啾,即中间沿的前面部分为低频率,后面部分为高频率;由于正常色散,低频率的群速度比高频率的快,因此先出现的低频率越来越快,后面的高频率本来出现的就慢跑的也慢,因此中间沿部分的低频、高频差距越来越大,导致中间沿部分被展宽。
3、后沿
后沿可以和前沿有差不多的理解,也是被压缩。
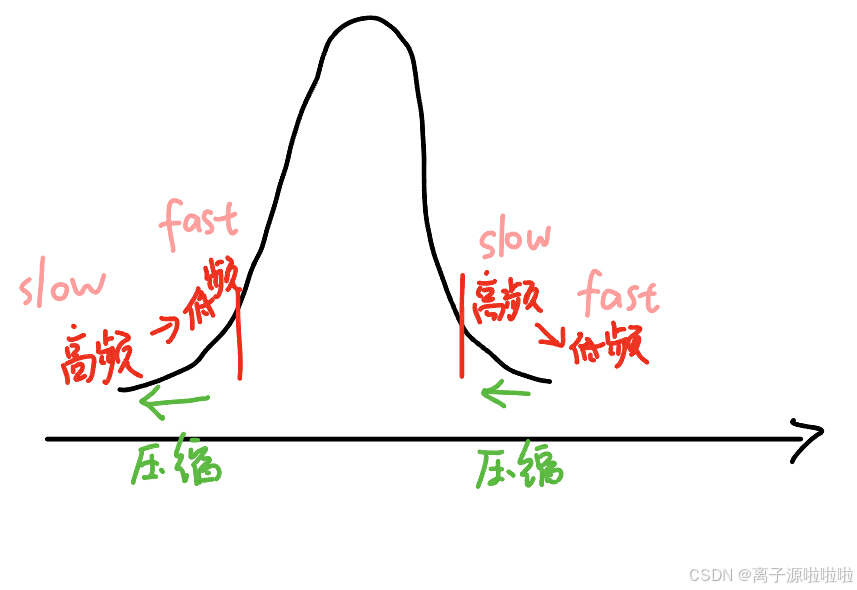
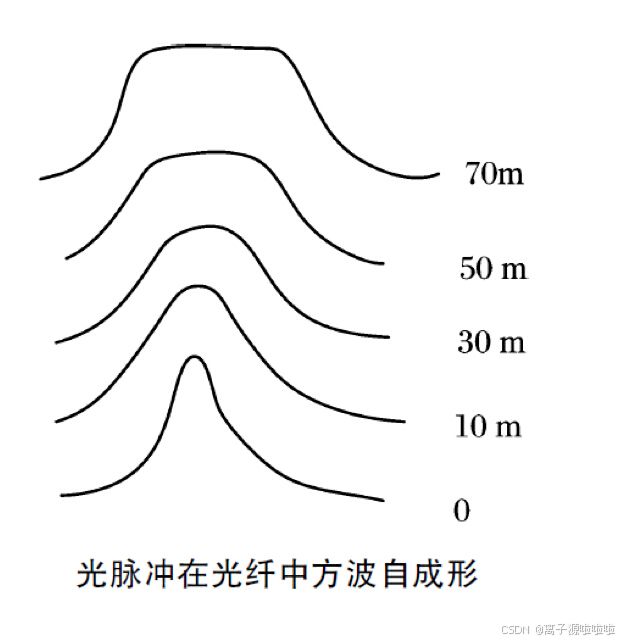
因此高斯脉冲光经过正常色散的介质,前后沿被压缩,中间沿被展宽,随着时间的推移,逐渐变成方波。
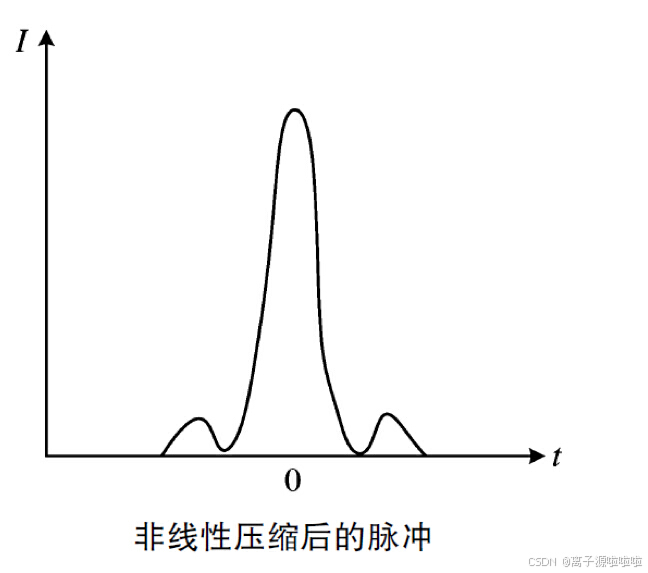
反常色散介质(压缩脉冲)
反常色散介质与正常色散介质完全相反
1、前沿
前沿为负啁啾,即前沿的前部分为高频率,前沿的后部分为低频率(可以理解为高频率先出现,低频率隔了一段时间才出现);而由于反常色散,高频率的群速度比低频率的快,前面部分的高频率和后面部分的低频率相差越来越大,脉冲前沿展宽
2、中间沿
中间沿为正啁啾,即中间沿的前面部分为低频率,后面部分为高频率;由于反常色散,高频率的群速度比低频率的快,因此先出现的低频率跑得慢,高频率群速度大,往前压缩,因此中间沿被压缩。
3、后沿
后沿可以和前沿有差不多的理解,也是被展宽。
五、孤子脉冲的形成
回到前面的光脉冲中某个频率的模式:
孤子其实就是色散和SPM的平衡即非线性压缩作用与k''产生的扩展相平衡就是一阶孤子的产生(稳定不变);
当非线性压缩作用大于k‘’产生的扩展,就产生高阶孤子(演化过程有周期性)




























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










