数据结构——跳表和散列

瑞-板凳精神

已于 2022-05-25 15:23:44 修改

阅读量644

点赞数

分类专栏：笔记 c++ 文章标签：算法数据结构

于 2021-04-16 12:00:26 首次发布

本文链接：https://blog.csdn.net/m0_51543618/article/details/115740841

版权

笔记同时被 2 个专栏收录

109 篇文章 1 订阅

订阅专栏

c++

64 篇文章 0 订阅

订阅专栏

虽然在n个元素的有序数组上折半查找所需要的时间为O(logn)，但是在有序链表上查找所需要的时间为O(n)。
为了提高有序链表的查找性能，可以在全部或部分节点上增加额外的指针。在查找时，通过这些指针，可以跳过链表的若千个节点，不必从左到右连续查看所有节点。
增加了额外的向前指针的链表叫做跳表(skiplist)。它采用随机技术来决定链表的哪些节点应增加向前指针，以及增加多少个指针。基于这种随机技术，跳表的查找、插入、删除的平均时间复杂度为O(logn)。然而，最坏情况下的时间复杂度却变成O(n)。
散列是用来查找、插入、删除的另一种随机方法。与跳表相比，它把操作时间提高Θ(1)，但最坏情况下的时间仍为Θ(n)。
C++的STL中使用了散列的容器类有: hash_ map、hash_multimap、hash_ multiset、 hash_ set。

有序数组、有序链表、跳表和哈希表的渐近性能汇总

在这里插入图片描述

字典

抽象类dictionary

template<class K，class E>
class dictionary
{
public:
	virtual ~dictionary() {}
	virtual bool empty() const = 0;
	//返回true， 当且仅当字典为空
	virtual int size() const = 0;
	//返回字典中数对的数目
	virtual pair<const K，E>* find(const K&) const = 0;
	//返回匹配数对的指针
	virtual void erase (const K&) = 0;
	//删除匹配的数对
	virtual void insert (const pair<const K，E>&) = 0;
	//往字典中插入一个数对
};

线性表描述

sortedChain的节点是pairNode的实例。pairNode 的实例有两个域：element 和next, 它们的类型分别是 pair<const K,E> 和 pairNode<K,E>*。

方法sortedChain<K,E>::find

template<class K，class E>
pair<const K,E>* sortedChain<K,E>:: find(const K& theKey) const
{//返回匹配的数对的指针
	//如果不存在匹配的数对，则返回NULL
	pairNode<K,E>* currentNode = firstNode;
	//搜索关键字为theKey的数对
	while (currentNode != NULL && currentNode->element. first != theKey)
		currentNode = currentNode->next;
	//判断是否匹配
	if (currentNode != NULL && currentNode->element. first == theKey)
		//找到匹配数对
		return &currentNode->element;
	//无匹配的数对
	return NULL;
}

方法sortedChain<K,E>:：insert

template<class K，class E>
void sortedChain<K,E>: :insert (const pair<const K，E>& thePair)
{//往字典中插入thePair,覆盖已经存在的匹配的数对
	pairNode<K,E> *p = firstNode , *tp = NULL;
	//移动指针tp,使thePair可以插在tp的后面
	while (P != NULL && p->element.first < thePair. first)
	{
		tp=p;
		P = p->next;
	}
	//检查是否有匹配的数对
	if (P != NULL G& p->element.first == thePair. first)
	{//替换旧值
		p->element.second = thePair.second;
		return;
	}
	//无匹配的数对，为thePair建立新节点
	pairNode<K,E> *newNode = new pairNode<K, E> (thePair, p) ;
	//在tp之后插入新节点
	if (tp == NULL) 
		firstNode = newNode ;
	else 
		tp->next = newNode; 
	dSize++;
	return;
}

方法sortedChain<K,E>::erase

template<class K，class E>
void sortedChain<K,E>::erase (const K& theKey)
{//删除关键字为theKey的数对
	pairNode<K,E> *p = firstNode, *tp = NULL;
	//搜索关键字为theKey的数对
	while (P != NULL && p->element.first < theKey)
	{
		tp=p;
		P = p->next;
	}
	//确定是否匹配
	if (P != NULL && p->element. first == theKey)
	{//找到一个匹配的数对
		//从链表中删除p
		if (tp == NULL) 
			firstNode = p->next;
		//p是第一个节点
		else 
			tp->next = p->next;
		delete P;
		dSize--;
	}
}

散列表描述

字典的另一种表示方法是散列( hashing)。它用一个散列函数(也称哈希函数)把字典的数对映射到一个散列表( 也称哈希表)的具体位置。
如果数对p的关键字是k，散列函数为f, 那么在理想情况下，p在散列表中的位置为f(k)。

散列函数

散列表的每一个位置叫一个桶( bucket ); 对关键字为k的数对：f(k) 是起始桶( home bucket);桶的数量等于散列表的长度或大小。因为散列函数可以把若千个关键字映射到同一个桶，所以桶要能够容纳多个数对。
本章我们考虑两种极端情况。第一种情况是每一个桶只能存储一个数对。第二种情况是每一个桶都是一个可以容纳全部数对的线性表。

除法散列函数

在多种散列函数中，最常用的是除法散列函数，它的形式如下: f(k)=k%D
其中k是关键字，D是散列表的长度(即桶的数量)，%为求模操作符。
散列表的位置索引从0到D-1。
当D=11 时，与关键字3，22，27，40，80，96分别对应的起始桶是f(3)=3, f(22)=0，f(27)=5， f(40)=7、f(80)=3 和f(96)=8。
起始桶的值都在范围内。

均匀散列函数

函数f(k)=k%D对范围[0,r]内的关键字是均匀散列函数，其中r是正整数。
当D可以被诸如3、5和7这样的小奇数整除时，不会产生良好散列函数。因此，要使除法散列函数成为良好散列函数，**你要选择的除数D应该既不是偶数又不能被小的奇数整除。理想的D是一个素数。**当你不能用心算找到一个接近散列表长度的素数时，你应该选择.不能被2和19之间的数整除的D。
因为在实际应用的字典中，关键字是相互关联的，所以你所选择的均匀散列函数，其值应该依赖关键字的所有位(而不是仅仅取决于前几位，或后几位，或中间几位)。当使用除法散列函数时，选择除数D为奇数，可以使散列值依赖关键字的所有位。当D既是素数又不能被小于20的数整除, 就能得到良好散列函数。

把一个字符串转换为一个不唯一的整数

int stringToInt(string s)
{//把s转换为一个非负整数，这种转换依赖s的所有字符
	int length = (int) s. length() ;
	//s中的字符个数
	int answer = 0;
	if (length%2 == 1)
	{//长度为奇数
		answer = s.at(length - 1) ;
		length--;
	}
	//长度是偶数
	for(int i=0;i<length;i+=2)
	{//同时转换两个字符
		answer += s.at(i) ;
		answer += ((int) s.at(i + 1)) << 8;
	}
	return (answer < 0) ? -answer : answer ;
}

线性探查

解决溢出的方法叫作线性探查( Linear Probing )。在寻找下一个可用桶时，散列表被视为环形表。
假设要查找关键字为k的数对，首先搜索起始桶f(k)，然后把散列表当做环表继续搜索下一个桶，直到以下情况之一发生为止:
1。存有关键字k的桶已找到，即找到了要查找的数对;
2。到达一个空桶;
3。又回到起始桶f(k)。
后两种情况说明关键字为k的数对不存在。
删除需要移动若干个数对。从删除位置的下一个桶开始，逐个检查每个桶，以确定要移动的元素，直至到达一个空桶或回到删除位置为止。在做删除移动时，一定要注意，不要把一个数对移到它的起始桶之前，否则，对这个数对的查找就可能失败。

线性探查的C++实现，hashTable 的数据成员和构造函数

这个类使用了线性探查法。注意，散列表用一维数组table[]表示，类型为pair<const K,E>*。

//散列表的数据成员
pair<const K，E>** table; //散列表
hash<K> hash; //把类型K映射到一个非整数
int dSize; //字典中数对个数
int divisor; //散列函数除数

//构造函数
template<class K，class E>
hashTable<K,E>::hashTable(int theDivisor)
{
	divisor = theDivisor;
	dSize = 0;
	//分配和初始化散列表数组
	table = new pair<const K，E>* [divisor] ;
	for (int i = 0; i < divisor; i++)
		table[i] = NULL;
}

hashTable<K,E>::search

template<class K，class E>
int hashTable<K,E>::search(const K& theKey) const
{//搜索一个公开地址散列表，查找关键字为theKey的数对
	//如果匹配的数对存在，返回它的位置，否则，如果散列表不满，
	//则返回关键字为theKey的数对可以插入的位置
	int i = (int) hash(theKey)%divisor; //起始桶
	int j=i;
	//从起始桶开始
	do
	{
		if (table[j] == NULL 1 table[jl->first == theKey)
			return j ;
		j =(j+ 1)%divisor; //下一个桶
	}while(j!=i); //是否返回到起始桶?
	return j ; //表满
}

hashTable<K, E>::find

template<class K，class E>
pair<const K,E>* hashTable<K,E>::find(const K& theKey) const
{//返回匹配数对的指针
	//如果匹配数对不存在，返回NULL
	//搜索散列表
	int b = search(theKey) ;
	//判断table[b]是否是匹配数对
	if (table[b] == NULL || table[b]->first != theKey)
		return NULL; //没有找到
		
	return table[b]; //找到匹配数对

hashTable<K,E>：:insert

template<class K，class E>
void hashTable<K, E>::insert(const pair<const K，E>& thePair)
{//把数对thePair插入字典。若存在关键字相同的数对。则覆盖
	//若表满，则抛出异常
	//搜索散列表。查找匹配的数对
	int b = search(thePair.first) ;
	//检查匹配的数对是否存在
	if (table[b] == NULL) .
	//没有匹配的数对，而且表不满
	{
		table [b] = new pair<const K,E> (thePair) ;
		dSize++;
	}
	else
	{//检查是否有重复的关键字数对或是否表满
		if (table[b]->first == thePair.first)
		{//有重复的关键字数对，修改table[b]->second
			table[b]->second = thePair.second;
		}
		else  //表满
			throw hashTableFull() ;
	}
}

性能分析

就平均性能而言，散列远远优于线性表。令U和S分别表示在一次不成功搜索和成功搜索中平均搜索的桶数，其中n是很大的值。这个平均值是由插人的n个关键字计算得来的。对于线性探查，有如下近似公式:
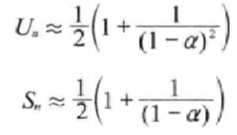
其中 a=n/b 为负载因子( loading factor)。

例子

设计一个可容纳近1000个数对的散列表。要求成功搜索时的平均搜索桶数不得超过4，不成功搜索时的平均搜索桶数不得超过50.5。由U的公式，得到a≤0.9，由S的公式，得到4≥0.5+1/(2(1-a))或a≤6/7。因此，a≤min{0.9，6/7}=6/7。因此b最小为[7n/61]（向上取整）=1167。b=D=1171 是一个合适的值。
另一种计算D的方法是，根据散列表可用空间的最大值来确定b的最大可能值, 然后取D为不大于b的最大整数，而且要么是素数，要么不能被小于20的数整除。例如，如果散列表最多有530个桶，则23*23=529是D和b的最佳选择。

链式散列

在这里插入图片描述

跳表表示

在一个用有序链表描述的n个数对的字典中进行查找，至多需要n次关键字比较。
如果在链表的中部节点加一个指针，则比较次数可以减少到n/2+1。这时，为了查找一个数对，首先与中间的数对比较。如果查找的数对关键字比较小，则仅在链表的左半部分继续查找，否则，在链表右半部分继续查找。
对n个数对而言，0级链表包括所有数对，1 级链表每2个数对取一个，2级链表每4个数对取一个，i级链表每2^i 个数对取一个。
一个数对属于i级链表，当且仅当它属于0 ~ i 级链表，但不属于i+1级(若该链表存在)链表。
我们把诸如图10-1c的结构称为跳表。在该结构中有一组等级链表。0级链表包含所有数对，1级链表的数对是0级链表数对的一个子集。
i级链表的数对是i-1级链表数对的子集。
图10-1c是跳表的一个规则结构，i 级链表所有的数对均属于i-1级链表。

插入和删除

在插入和删除时，要保持图10-1c跳表的规则结构，需要耗时O(n)。在规则的跳表结构中，i级链表有 n/2^i 个记录，在插入时要尽量逼近这种结构。
插入的新数对属于i级链表的概率为1/2^i 。在实际确定新数对所属的链表级别时，应考虑各种可能的情况。把新数对插入i级链表的可能性为p ^i .
在图10-1c中，p=0.5。对一般的p，链表的级数为[ logw1/p(n) ]（向下取整）+1。
在一个规则的跳表中，i级链表包含1/p个i-1级链表的节点。
在插入时，要为新数对分配一个级(即确定它属于哪一级链表), 分配过程由后面将要介绍的随机数生成器来完成。若新数对属于i级链表，则插入结果仅影响由虚线切割的0 ~ i级链表指针。图10-1e是插人77的结果。

级的分配

在规则的跳表结构中，i-l 级链表的数对个数与i级链表的数对个数之比是一个分数p。因此，属于i-1级链表的数对同时属于i级链表的概率为p。
假设用一个统一的随机数生成器产生0和1间的实数，产生的随机数≤p的概率为p。若下一个随机数≤p,则新数对应在1级链表上。要确定该数对是否在2级链表上，要由下一个随机数来决定。若新的随机数≤p,则该元素也属于2级链表。重复这个过程，直到一个随机数>p为止。
这种方法有潜在的缺点，某些数对被分配的级数可能特别大，远远超过log1/p(N),其中N为字典数对的最大预期数目。为避免这种情况，可以设定一个级数的上限maxLevel, 最大值为[ log1/p(N) ]（向上取整）- 1
这种方法还有一个缺点，即使采用了级数的上限maxLevel,还可能出现这样的情况:在插入一个新数对之前有3个链表，而在插人之后就有了10个链表。也就是说，尽管3 ~ 8级链表没有数对，新数对却被分配到9级链表。换句话说，在插入前后，没有3 ~ 8级链表。因为这些空级链表并没有什么好处，我们可以把新记录的链表等级调整为3。

文件压缩（LZW）

在这里插入图片描述

LZW压缩方法把文本字符串映射为数字编码。首先，该文本串中所有可能出现的字母都被分配个代码。例如，要压缩的文本串是S=aabbbbbaabaaba,它由字符a和b组成，a的代码是0, b的代码是1。
字符串和编码的映射关系存储在一个数对字典中，每个数对形如( key, value),其中key是字符串，value 是该字符串的代码。

瑞-板凳精神

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
2
评论
数据结构——跳表和散列

虽然在n个元素的有序数组上折半查找所需要的时间为O(logn)，但是在有序链表上查找所需要的时间为O(n)。为了提高有序链表的查找性能，可以在全部或部分节点上增加额外的指针。在查找时，通过这些指针，可以跳过链表的若千个节点，不必从左到右连续查看所有节点。增加了额外的向前指针的链表叫做跳表(skiplist)。它采用随机技术来决定链表的哪些节点应增加向前指针，以及增加多少个指针。基于这种随机技术，跳表的查找、插入、删除的平均时间复杂度为O(logn)。然而，最坏情况下的时间复杂度却变成O(n)。散列是.
复制链接

扫一扫