【数字设计与计算机体系结构】2021-09-26-数字设计与计算机体系结构课程（四）

一、计算机中的数制

1.1：进位计数制

数制	数码	权	基数	书写后缀
十进制	（0~9）	10k	10	D / d / ()10
二进制	（0~1）	2k	2	B / b / ()2
八进制	（0~7）	8k	8	O / o / ()8
十六进制	（0~15）	16k	16	H / h / ()16

1. 进位计数制表示方法：
   以二进制为例：（N）₂=D_n-1×2^n-1+D_n-2×2^n-2+D_n-3×2^n-3+……+D_m×2^-m;
   其中，n为整数位，m为小数位；
2. 进位计数制口诀:
   以十进制为例：逢十进一，借一当十;
3. 与十进制相同，R进制位数中，所有数位向左移动一格等同于原数×R，向右同理;
4. 各个进制数对应关系：
   

1.2：进制间转换

1. R进制转换为十进制：
   (M)_R ＝ (K_n-1×R_n-1 ＋ K_n-2 ×R_n-2 ＋ … ＋K₁×R₁＋ K₀ ×R₀＋K_-1 ×R_-1＋K_-2 ×R_-2＋… ＋K_-m×R_-m )₁₀；
2. 十进制转换为R进制：
   对十进制的整数部分的转换： 采用“除R取余”的方法，直至商为零；
   注意是商为零，不一定除得尽；建议使用短除法，然后把除出来的各个商依次从低到高排序排好，这样就完成了整数部分的转换；
   对十进制的小数部分的转换： 采取“乘R取整”的办法，每次乘出来一个整数就填到最近一位小数位里，直至小数部分为零或者满足要求的精度（因为可能会无法消除小数部分）；

3. 二级制转换为十六进制：
   以小数点为中心点，
   整数部分：从右向左每4位一组，最高一组如果不足4位的左边补0；
   小数部分：从左向右每4位一组，最低有效位不足4位时在右边补0；
   然后将每组4位二进制数用等值的一位十六进制数替换 。
   

4. 十六进制转换为二进制：
   以小数点为中心点，
   整数部分：从右向左每一位十六进制数用等值的4位二进制来取代；
   小数部分：从左向右每一位十六进制数用等值的4位二进制来取代；

【二进制与八进制之间的转换与十六进制类似，只不过是四比一换成了三比一；进制部分没什么可讲的，所见即所得的东西，只不过今天我会用Markdown搞表格和公式了，算是写作中的进步（小开心）；有一个小问题就是当十六进制或者八进制转换为二进制的时候是否有多种可能，不过想来】

二、计算机中数的表示

2.1： 计算机中

计算机中采取二进制数，逻辑“1”和“0”的表示，最容易逻辑实现和最便于存储。

1. 电压的高低、半导体工艺，CMOS（电脑的一种芯片）；
2. 用磁通量的有无表示，超导体工艺；
3. 用能级的高低表示，量子计算机；

2.2：位，半字节，字节，字，字长，模

1. 位(bit)： 存储、传送的一个二进制位（0或1）；
2. 半字节(Nibbles): 4个二进制位组成半字节，表示24=16个数，现在不常用；
3. 字节(Byte): 8个二进制位组成字节，表示28=256个数；
4. 字(Word): 微处理器一次处理数据的块大小，它取决于微处理器的体系结构；
5. 字长： 运算器(ALU)的位数（宽度）——电路决定，32位ARM的字长是32，它包含4个字节；
6. 模: 二进制模2，十六进制模16，字长为n的二进制数运算是模2ⁿ运算；

【这里字长这个概念有点夹缠不清，我理解下来就是CPU一次能并行处理的二进制位数，比如字长为16则一次能处理十六位；（百科上的类比：我们先来看一下人脑是如何进行计算的，例如5×6则立即可以得到答案是30，但对于55×66，就不可能立即得到正确的答案，这就是说55或66已走出了人脑的“字长”，这是为了得出结果，就必须把复杂的问题（如55×66）分解成易于处理的问题（如55×66可分解为50×60，50×6，5×60，5×6），然后再综合起来，得出结果。）对于一台16字长的计算机，2¹⁶以内的数就可以直接处理了，以上的一步就无法处理。】

2.3：计算机中存储的数据

1. 存储器存数据以字节为单位，每字节都有一个唯一的地址;
2. 对于n位二进制数，权为2⁰=1的位称为最低有效位(lsb)，权为2^n-1的位称为最高有效位(msb);
3. 一个多字节的数据（比如一个字）存储时，分别占据相邻的多个字节，最低地址是该数据的地址。最低有效字节是LSB，最高有效字节是MSB。
   
4. 一些二的幂次的对比：
   2¹⁰=1024≈10³=1K ;
   2²⁰≈10⁶=1M(兆)；
   2³⁰≈10⁹=1G (吉);
   2⁴⁰≈10¹²=1T (太);
   2⁵⁰≈10¹⁵=1P (拍)；
   注意：Mb是兆位，MB是兆字节。

【有个问题就是最低地址是什么？我理解中是第一个字节中的地址；】

5. 多字节数据的存取：
   大端存储： 低字节放在高地址，高字节放在低地址；
   小端存储： 低字节放在低地址，高字节放在高地址；
6. 数据存放的对齐机制：
   如果一个K字节的数据存放的时候地址是K的整数倍，则称该数据是边界对齐的，边界对齐的双字节数据地址为偶数，4字节地址是4的倍数。如果过采用边界不对齐存放数据，可能会影响数据的访问速度。（访问几个线程问题）
   
   【其实还是不太懂这里是怎么一个对齐法，因为老师配的图，有点和我理解的不太能对的上】
   这个图就有点迷：
   
7. PC机中的数据及存放：
   位 1 bit=1个二进制位
   字节 1 Byte=8 bit；
   字 1 Word=2 Byte ；
   双字 1 Doubleword=2 Word；
   四字 1 Quardword=4 Word；
   十字节 1 TenByte=10 Byte；
   采用小端存储；

例如：

0000H地址上，字节数据是12H，字数据是3412H，双字数据是78563412H，四字数据是FFDEBC9A78563412H。

2.4：数与码

2.4.1：有符号数

1. 无符号数：普通的二进制数，数值范围为0和正数；
   有符号数：数值第一位为正负标号，数值范围为0和正负数；
2. 有符号数的机器数和真值：
   真值： 现实中有+、-号加上数的绝对值，如+37、-65；
   机器数： 计算机中使用、连同符号位一起数字化的数，用特定的二进制代码表示，其最高位为符号位，正数为“0”、负数为“1”，如+37机器数为00100101（此为八位有符号二进制数）；

2.4.2：三种码

2.4.2.1：原码

1. 原码：原码就是将最高位作为符号位，最高位为0表示正数，最高位为1表示负数，符号位后面是该数的绝对值。
   $$[X{]}_{原码}=\{\begin{array}{ll}X，& \text{0≤X≤ 2n−1−1 }\\ 2^{n-1}+|X|，& \text{− ( 2n−1−1)≤X≤0}\end{array}$$
   例子：

正数	负数
[+37]原 = 00100101	[-37]原 = 10100101
[+127]原 = 01111111	[-127]原 = 11111111
[+0]原 = 00000000	[-0]原 = 10000000

$$原码：\{\begin{array}{ll}优点：& \text{简单易懂，与真值之间转换以及做乘、除运算都比较方便。 }\\ 缺点：& \text{如出现两个异号相加，或者同号相减，则不仅要做减法器，还要根据两数绝对值的大小决定结果的符号。}\end{array}$$

2.4.2.2：反码

1. 正数： 反码和原码相同；
2. 负数： 反码是与它绝对值相等的正数连同符号位按位取反。

$$[X{]}_{反码}=\{\begin{array}{ll}X，& \text{0≤X≤ 2n−1−1 }\\ 2^{n-1}+X，& \text{− ( 2n−1−1)≤X≤0}\end{array}$$

例子：

正数	负数
[+37]反 =00100101	[-37]反 =11011010
[+127]反 =01111111	[-127]反 =10000000
[+0]反 =00000000	[-0]反 =11111111

PS：反码运算很不方便，和原码一样，0的表示也不唯一，通常只是一种过渡码，比如负数从原码变为补码的时候先转为反码。

2.4.2.3：补码

1. 正数： 补码与其原码相同；
2. 负数： 补码为符号位的1不变，后面的数与它的绝对值相等的正数的数值位按位取反加1（求补数）。

$$[X{]}_{补码}（mod{2}^n）=\{\begin{array}{ll}X，& \text{0≤X≤ 2n−1−1 }\\ 2^n+X，& \text{− ( 2n−1)≤X≤0}\end{array}$$
例子：

正数	负数
[+37]补 =00100101	[-37]补 =11011011
[+127]补 =01111111	[-127]补 =10000001
[+0]补 =00000000	[-128]补 =10000000

特点：

1. 负数的表示范围比原码和反码多1个；
2. 0的表示是唯一的，便于运算。

【这里取反之后加一如果溢出了该怎么办……但是想来好像也只有0有这个情况，好像是特事特办了……先放放，今天学写公式学的头都大了，先去写写统计学习方法。】

关于补码：
计算机中的二进制数用补码来表示，优点是：

1. 负数的补码与对应正数的补码之间的转换可用同一方法：求补运算实现，因而可简化硬件；
2. 可将减法变为加法运算，从而省去减法器；
3. 有符号数和无符号数的加法运算可用同一加法器电路完成，结果都正确；

PS：补码的基础：
【补数： 以M为模（模是一个计量系统的计数范围），则A=M-B的话，A与B互为补数，如12为模则7和5互为补数，10为模则6和4互为补数。记A的补数为A’；则有：A-B = A-B+M (mod M) = A+(M-B)(mod M) = A+B’(mod M) 例如10为模运算：7-2=7+8（mod 10）= 5】

【仅仅就补码的构造而言（暂且先不谈构造补码出来有什么意义以及补码的应用），补码的存在可以简单地用一些最基础的数论来理解：7与-5都是同余12模7，那么原码变成补码的过程就是把-5这个数变换成7的过程，在这里就是同余2ⁿ，而n-1位二进制数最多就是n-1个1，即2ⁿ-1,所以原码变反码还是反码变原码都得加一。】

下面开始理解补码的应用：

1. 一个简单的求补方法：
   正数不变，负数符号位不变，数值位从右开始向左找到第一个1，该位及右边的位不变，该位左边的各位（除符号位）取反。

补码的运算：

1. 补码运算基本规则
   [A+B]补=[A]补+[B]补，[A-B]补=[A]补-[B]补。
2. 补码运算三种情况：

一、 A=B+C (两个正数相加）
【采用补码系统计算和采用原码系统计算结果一致，如果运算后符号位为1，则溢出】

二、 A=B-C (一个正数减去一个正数=一个正数加上一个负数）
A = B-C = B+(-C) = B+[-C]补
【不会产生溢出，如有进位，舍去即可】

三、 补码运算三种情况
A=-B-C (一个负数减去一个正数）
A = [-B]补+[-C]补(两个负数相加)
如果运算后符号位为0，则溢出；

有符号数加法总结：
1.两正数相加结果为负数，溢出
2.两负数相加结果为正数，溢出
3.一正一负相加不会溢出

【说实在的，关于是否溢出的问题我还是不是很懂，理解了，但是没有完全理解】

2.4.3：计算机中的码

1. 定义：
   码是一种表示信息的方法，它有一定的规则；
   计算机中的码是用一组二进制数(或16进制数)按一定规则排列起来以表示数字、符号等特定信息。
2. 数值码：

一、自然二进制码

按自然数顺序排列的二进制码
常用四位自然二进制码，表示十进制数0~15，各位的权值依次为2³、2²、2¹、2⁰。

二、格雷码

任意两组相邻码之间只有一位不同。首尾两个数码即最小数0000和最大数1000之间也符合此特点，故它可称为循环码；
格雷码属于可靠性编码，相邻编码只有一位变化，避免了过渡码产生的“噪声”是一种错误最小化的编码方式。
说不如写：

十进制	自然二进制	格雷码
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

【说实在的，自然二进制和格雷码对比没有什么什么意义，因为格雷码也不是从自然二进制改过来的，可以自己写一遍，坚持格雷码的原则就不会出什么问题】

三、定点数，浮点数

定点数
用于表示带符号的整数或纯小数
整数表示：
符号位.2ⁿ⁻¹2ⁿ⁻²…2¹2⁰.
如 11101010 = -0010110;
纯小数表示
符号位.2⁻¹2⁻²…2⁻⁽ⁿ⁻²⁾2⁻⁽ⁿ⁻¹⁾.
如 11101010= -0010110(-0.0010110）
浮点数
是数的科学表示法
N=M×2^E

【这里定点数浮点数看的有点迷糊，但是好像不是那么重要，所以不在这里纠结了，继续了】

四 、BCD码

1. 定义： BCD码是一种以4位二进制形式编码1位十进制数码；
2. 有权码：
   四位二进制数中的每一位都对应有固定的权，每一位的1在不同代码中代表固定的数值；
   8421 BCD码(NBCD码)
   4位的权值分别为8,4,2,1，如1001=1×8+0×4+0×2+1×1=9；
   8位8421 BCD码表示2位10进制数，如79=0111 1001；
   2421 BCD码
   4位权值分别为2,4,2,1；
   5421 BCD码
   4位权值分别为5,4,2,1；
3. 无权码
   四位二进制数中的每一位没有固定的权；
   余3码
   是8421 BCD码的每个码加3(0011)形成的。
   余3循环码
   余3循环码是变权码，每一位的1并不代表固定的数值。
   将格雷码中的3~12的编码00101010,作为0至9的余3循环码.
   它具有格雷码的优点，即两个相邻代码之间仅有一位的状态不同。

五、字符码

1. ASCII码
   目前计算机用的最广的字符集及其编码
   用8位二进制的低7位表示128个字符
   
   
   
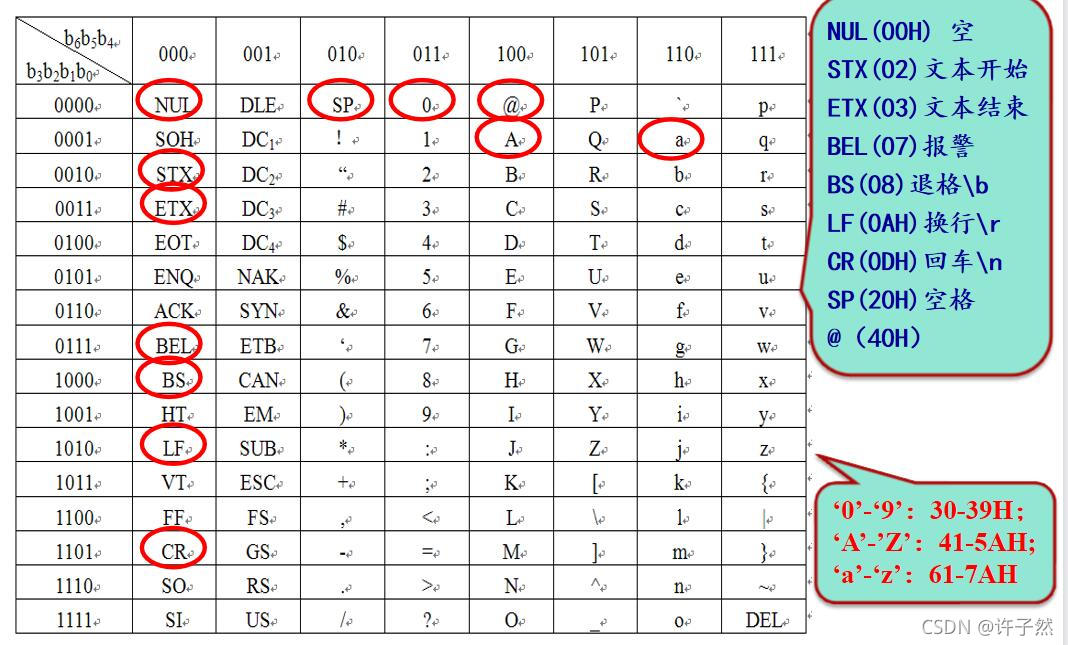
   实在不清楚到底哪个更加标准，也不想在这里多花时间，就这么操作了。
2. 汉字国标码
   两个字节表示；
   GB2312-80 （《信息交换用汉字编码字符集 基本集》）国标码共有6763个汉字（基本集）；
   纵坐标(7bit)，横坐标(8bit) ；
   纵坐标(30)₁₆,横坐标(7C)₁₆的位置是“包”字，则其国标码为(307C)₁₆；
   94个区号和位号，形成区位码；

三、 数字系统与逻辑门

3.1逻辑门

数字抽象后的形象化：门。

1. 逻辑门（最简单的数字电路）：接受一个或多个二进制输入并产生一个二进制输出；输入与输出的关系用真值表或者布尔表达式描述。
2. 真值表：左边列出输入，右边列出输出，每种可能的组合对应一行；
3. 布尔表达式：基于二进制变量的数学表达式；

3.1.1：非门（非逻辑）

1. 定义：逻辑否定：某一事件前提条件不成立的时候，该事件却为真，反之为假；
2. 逻辑符号：
   
3. 概念电路：
   
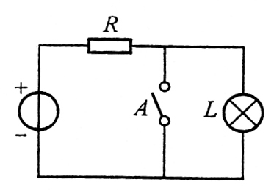
4. 真值表：

A	F
0	1
1	0

5. 逻辑表达式：F=$\overline{\text{A}}$（非逻辑运算符）

3.1.2：与门（与逻辑）

1. 定义：又称为逻辑乘：某一事件的所有前提条件都成立，该事件才为真，反之为假；

2. 逻辑符号：

3. 概念电路：
   

4. 真值表：

A	B	F
0	0	0
0	1	0
1	0	0
1	1	1

5. 逻辑表达式：
   F=A∙B ； F=A×B ； F=AB ； F=A∧B ； F=A∩B；
   都是一个意思，而且甚至运算符也可以省略；

3.1.3：或门（或逻辑）

1. 定义：又称为逻辑加：某一事件的任一或几个前提条件成立，该事件就为真，反之为假；

2. 逻辑符号：

3. 概念电路：
   

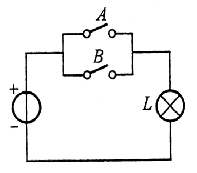
4. 真值表：

A	B	F
0	0	0
0	1	1
1	0	1
1	1	1

5. 逻辑表达式：F=A+B F=A∨B F=A∪B

3.1.4：缓冲器

单输入逻辑门，仅仅输出输入的东西，不做任何变化（仅仅就结果而言）；
在这个层次的抽象上缓冲器的确没有什么作用，在其他层次上才能体现出它对效率的作用。

3.1.5：基本逻辑运算

3.1.5.1：非运算

$\overline{\text{1}}$=0；
A ̿=A；（这里是A的非的非还是A本身，但是我不会打双上横线，只好凑合着看了）

3.1.5.2：与运算

A·0 = 0 ； A·1 = A
1·A = A ； 0·A = 0
A·A ̅= 0 ； A·A = A

3.1.5.3：或运算

A+0=A ； A+1=1
1+A=1 ； 0+A=A
A+A ̅=1 ； A+A=A

3.1.5.4：逻辑运算优先级

1. 非运算>与运算>或运算；
2. 括号能改变优先级；

3.1.6：与非门（与非逻辑）

1. 逻辑符号：
   
2. 真值表：

A	B	F
0	0	1
0	1	1
1	0	1
1	1	0

3. 逻辑表达式：F=$\overline{\text{A∙B}}$

3.1.7：或非门（或非逻辑）

逻辑符号：

真值表：

A	B	F
0	0	1
0	1	0
1	0	0
1	1	0

逻辑表达式：F=$\overline{\text{A+B}}$

3.1.8：异或门（异或逻辑）

逻辑符号：

真值表：

A	B	F
0	0	0
0	1	1
1	0	1
1	1	0

逻辑表达式：F=A⨁B=A$\overline{\text{B}}$+B$\overline{\text{A}}$

3.1.9：同或门（同或逻辑）

逻辑符号：

真值表：

A	B	F
0	0	1
0	1	0
1	0	0
1	1	1

逻辑表达式：F=A⨀B=(A⨁B) 的非=AB+$\overline{\text{A}}$ $\overline{\text{B}}$

3.1.10：其他逻辑

1. 与或逻辑：
   逻辑表达式：
   F=A∙B+C∙D=AB+CD；
2. 与或非逻辑：
   逻辑表达式：
   F=$\overline{\text{AB+CD}}$;

【本文主体内容到此结束，还有一些内容会在下一篇文章补充给出，真的是要写死了……不过也学会了很多，技术上成熟了不少。】

【END】