本文深入探讨了定点数的乘法和除法运算。介绍了从传统的笔算乘法到计算机优化的串行乘法和改进方法，包括恢复余数法和不恢复余数法的除法策略。详细阐述了每种方法的步骤和在计算机中的实现，对比了笔算与机器运算的差异，并讨论了数据约定和符号位处理。
目录
定点乘法运算
串行乘法
由手算的乘法过程引入，积的符号位单独运算，数值的结果取绝对值运算
- 符号位单独处理
- 乘数的某位决定是否加上乘数
- n位积一起相加
- 积的位数扩大乘数的位数倍
其中计算机可做1，2，4，但3相对复杂，具体如下图：
笔算乘法的改进
- 被乘数与乘数的每一位单独相乘，在逐个相加，再层层提取公因数
- 其中提取公因数的方法实际上是在进行右移操作
- 与串行乘法是一个原理，但是更便于计算机操做
具体如下图：
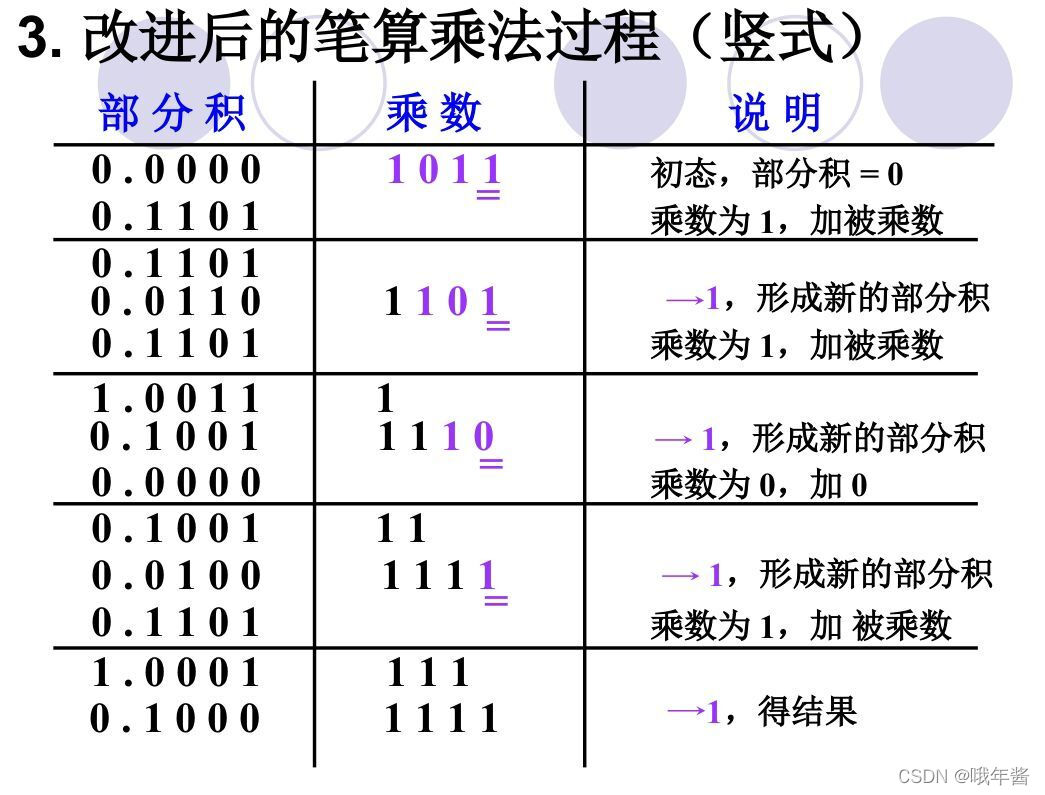
改进后的笔算乘法的过程
- 首先把被乘数和乘数分别列出来
- 判断乘数的最后一位，若为 1 ，则被乘数加上乘数，否则，被乘数加上 0
- 被乘数右移一位，乘数右移一位
- 乘数右移的过程中，最低位丢弃，最高位继承被乘数的最低位
- 充分上述过程，知道原乘数全部移完即可得到积
定点乘法运算的小结
定点乘法运算的实例
定点除法运算
分析笔算除法
- 商和数值位单独处理
- 通过比较大小决定上商为 1 ，还是 0
- 被除数不够位数时，在末位添加 0
下面是示范：
笔算除法与机器除法的比较
- 机器运算的符号位通过异或运算得出
- 笔算除法通过比较大小决定上商的值，但机器通过相减是否为负数来决定
- 比算时，余数在运算的时候不动，末端添数；机器运算时，余数通过左移一位，低位补 0 的方式，再加或减除数
具体如下图：
除法的数据约定
设被除数为 x，除数为 y
- 小数定点除法 |x| < |y| ,整数定点除法 |x| > |y| （避免商的溢出）
- 被除数不等于 0 ，除数不能为 0
原码恢复余数法
- 符号位不参与运算，结果的符号位由被除数和除数的符号位异或得出
- 首先 +[-|y|] 的补码
- 若结果为正数，则上商为 1， 余数左移一位
- 若结果为负数，则上商为 0， 余数 +[|y|] 的补码，再左移一位
- 重复上述操做直到商达到相应的精度
- 若最终余数为负，则需要恢复余数
恢复余数法运算的实例
原码不恢复余数法
- 符号位不参与运算，结果的符号位由被除数和除数的符号位异或得出
- 首先 +[-|y|] 的补码
- 若结果为正数，则上商为 1， 余数左移一位
- 若结果为负数，则上商为 0， 余数左移一位 ，再 +[|y|] 的补码
- 重复上述操做直到商达到相应的精度
- 若最终余数为负，则需要恢复余数
不恢复余数法运算的实例
补码加减交替法
- 符号位参与运算（通常采用双符号位）
- 被除数和除数同号，则被除数减去除数
- 被除数和除数异号，则被除数加上除数
- 余数与除数同号，上商 1，余数左移一位减去除数
- 余数与除数异号，上商 0，余数左移一位加上除数
- 商的最后一位恒置为 1 （方便，且误差不超过2^(-n),便于制造除法器）
补码加减交替法运算实例
双符号位的补充
- 双符号位主要用来判断运算结果是否溢出，非常方便
| 双符号 | 意义 |
| 00 | 正数 |
| 01 | 上溢 |
| 10 | 下溢 |
| 11 | 负数 |
扫一扫
7675
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
