平衡树学习笔记之 fhq Treap

平衡树学习笔记 1：fhq Treap（非旋 Treap）

正文开始前首先 %%% fhq 大佬。

众所周知，平衡树是一种 非常猥琐 码量堪忧的数据结构。
他的祖先是一种叫做二叉搜索树 ( $BST$ ) 的东东。
话说二叉搜索树是个什么玩意呢？

二叉搜索树：

显而易见，这是一棵二叉树 (逃),它的每个节点上有一个需要我们维护的值，我们称为“关键码”
然后这棵树的中序遍历是一个关于关键码的一个严格单调递增序列 (假设没有重复的元素) 是有序的。
然后就没了。
当然我们可以用这玩意来搞很多非常 恶心 有用的东西。

平衡树：

根据二叉搜索树的性质，我们可以递归查询每一个点的排名，排名为 k 的点，还可以支持动态插入，删除某个数，它的每次操作的 期望复杂度 是$O(logn)$因为一棵随机生成的BST的深度期望是 $logn$

但是我们操作二叉搜索树的时候发现了一些奇妙的东西：
比如说看这两张图：


显然前面这棵树它看起来更优一点，最后跑起来会比较快。
然后看一看极端数据，真是令人不寒而栗

你告诉我这和一条链有什么区别？
那么当你构造的BST 变成最后一个图这样，那你每次操作的复杂度最坏会达到 $O(n)$！
当然，我们发现有同样的BST 和这条链等效。

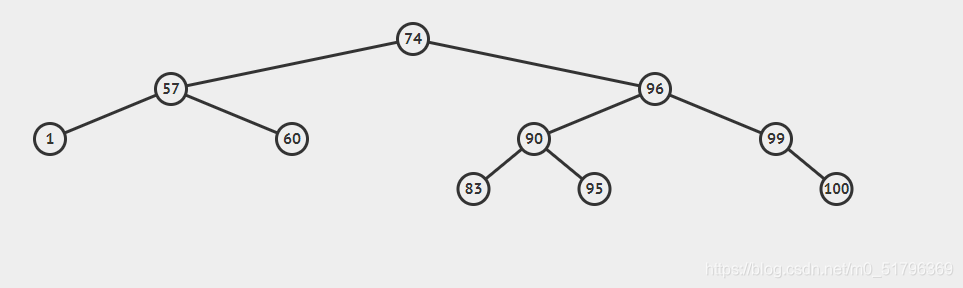
这两者是等效的，很明显后者得每次操作比前者更快，它的深度小。
所以我们把后者称为平衡树。
那么怎么维护一棵BST呢？

fhq Treap (非旋 Treap)

众所周知，有一种简单易懂的平衡树叫做 Treap，它在每一个点上弄了一个附加权值，这些附加权值满足 堆 的性质，而维护的权值满足 BST 的性质。
Treap 是使用旋转操作来维护堆的性质的，但是我这个人真心菜，被绕的晕晕乎乎的。
然后看到了 fhq 非旋 treap，感觉简单易懂，操作思路清晰，功能强大跑的还不慢，
就愉快的去学了一下。
一般的 treap 的附加权值是怎么搞得？怎么样才能使树平衡呢？
当然是：随机！！！
所以fhq treap 借用了 treap 的随机化思想，只用了两个基本操作就能实现一般平衡树的所有操作。

基本操作1：分裂 （split）

它的主要思想就是把一个Treap分成两个。
split 操作有两种类型，一种是按照权值分配，一种是按前k个（数量）分配。
第一种就是把所有小于k的权值的节点分到一棵树中，第二种是把前k个点分到一个树里。
放上代码

权值版：

void split(ll now,ll k,ll &x,ll &y) //将以now为根的树按照 k 分裂为根为x,y的两部分
{
	if(now==0) x=y=0; //节点为空
	else
	{
		if(val[now]<=k) // 当前节点的值比 k 小，那么他的左子树上的所有值也一定比 k 小
		{
			x=now; //根节点成为现在的节点
			split(rc[now],k,rc[now],y); //递归看右子树
		}
		else // 同理
		{
			y=now;
			split(lc[now],k,x,lc[now]);
		}
		update(now); //更新答案
	}
}

对于我们遍历到每一个点，假如它的权值小于k，那么它的所有左子树，都要分到左边的树里，然后遍历它的右儿子。假如大于k，把它的所有右子树分到右边的树里，遍历左儿子。
一般我们用的比较多的是权值版。

前 k 个的版本：
有点像主席树找第 k 大的代码。

void split(ll now,ll k,ll &x,ll &y) //将以now为根的树按照前 k 个点分裂为根为x,y的两部分
{
	if(now==0) x=y=0; //节点为空
	else
	{
		if(siz[now]+1<=k) //这里的siz后面写成了f
		{
			x=now; //根节点成为现在的节点
			split(rc[now],k-siz[now]-1,rc[now],y); //递归看右子树
			//k要减去左子树记录的个数
		}
		else // 同理
		{
			y=now;
			split(lc[now],k,x,lc[now]);
		}
		update(now); //更新答案
	}
}

基本操作2：合并（ merge ）

将split分开的两棵平衡树 treap 合并起来。
因为第一个Treap的权值都比较小，我们比较一下它的 pos (附加权值)，假如第一个的 pos 小，我们就可以直接保留它的所有左子树，接着把第一个 Treap 变成它的右儿子。反之，我们可以保留第二棵的所有右子树，指针指向左儿子。
你可以把这个过程形象的理解为在第一个Treap的左子树上插入第二个树，也可以理解为在第二个树的左子树上插入第一棵树。因为第一棵树都满足小于第二个树，所以就变成了比较pos来确定树的形态。
（转自 远航之曲 大佬）
代码很简洁：

ll make(ll x,ll y)
{
	if(x==0||y==0) return x+y; //返回其中有数的那棵树
	if(pos[x]<pos[y]) //pos 指的是优先级
	{
		rc[x]=make(rc[x],y);
		update(x);
		return x;
	}
	else 
	{
		lc[y]=make(x,lc[y]);
		update(y);
		return y;
	}
}

然后还有一堆平衡树的日常操作：

插入：

插入一个权值为v的点，把树按照v的权值split成两个，再按照顺序合并回去。

split(root,v,x,y);
root=make(make(x,getnew(v)),y);

删除：

稍微麻烦一点。
删除权值为v的点，把树按照v分成两个a,b,再把a按照v-1分成c,d。
把c的两个子儿子合并起来 (这时候那个点已经被删除了)，再$merge(merge(c,d),b)$，把分开的树合并回去。
有点绕自己好好理解。

split(root,v,x,z);
split(x,v-1,x,y);
y=make(lc[y],rc[y]);
root=make(make(x,y),z);

查找排名为 k 的数：

ll find(ll now,ll k) //now是树的根节点
{
	while(1+1==2)//c++划水写法
	{
		if(k<=f[lc[now]]) now=lc[now]; //比左子树要小
		else if(k==f[lc[now]]+1) return now;  //=左子树比他小的+1
		else k-=(f[lc[now]]+1),now=rc[now]; 
	}
}

查找前驱：

把root按v-1 split成x,y，在x里面找最大值。

split(root,v-1,x,y);
put(val[find(x,f[x])]); //1~v-1中最大的那个，也就是第f[x]的那个
root=make(x,y);

查找后继：

把root按 v split 成x,y，在y里面找最小值。

split(root,v,x,y);
put(val[find(y,1)]); //v+1~n 中的最小值
root=make(x,y);

查找 v 的排名：

把root按 v-1 split 成x,y，x 的 siz 大小+1

split(root,v-1,x,y);
put(f[x]+1); //左边都比现在的值小
root=make(x,y);

注意，对于在主函数中执行的 split 一般后面都会跟着相同数量的 merge (我写的是 make )

代码：

【洛谷 P3369】 普通平衡树

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<ctime>
#include<cstring>
#define r register
#define rep(i,x,y) for(r ll i=x;i<=y;++i)
#define per(i,x,y) for(r ll i=x;i>=y;--i)
using namespace std;
typedef long long ll;
const ll V=5e5+10;
ll t,x,y,k,z;
ll in()
{
	ll res=0,f=1;
	char ch;
	while((ch=getchar())<'0'||ch>'9')
	 if(ch=='-') f=-1;
	res=res*10+ch-48;
	while((ch=getchar())>='0'&&ch<='9')
	 res=res*10+ch-48;
	return res*f;
}
void put(ll x)
{
	if(x<0) putchar('-'),x*=-1;
	if(x>9) put(x/10);
	putchar(x%10+48);
}
ll lc[V],rc[V],val[V],f[V],pos[V];
ll cnt,opt,v,root;
void update(ll x)
{
	f[x]=f[lc[x]]+f[rc[x]]+1;
}
void split(ll now,ll k,ll &x,ll &y)
{
	if(now==0) x=y=0;
	else
	{
		if(val[now]<=k)
		{
			x=now;
			split(rc[now],k,rc[now],y);
		}
		else 
		{
			y=now;
			split(lc[now],k,x,lc[now]);
		}
		update(now);
	}
}
ll make(ll x,ll y)
{
	if(x==0||y==0) return x+y;
	if(pos[x]<pos[y])
	{
		rc[x]=make(rc[x],y);
		update(x);
		return x;
	}
	else 
	{
		lc[y]=make(x,lc[y]);
		update(y);
		return y;
	}
}
ll getnew(ll x)
{
	f[++cnt]=1;
	val[cnt]=x;
	pos[cnt]=rand()%1000000000+10;
	return cnt;
}
ll find(ll now,ll k)
{
	while(1+1==2)
	{
		if(k<=f[lc[now]]) now=lc[now];
		else if(k==f[lc[now]]+1) return now;
		else k-=(f[lc[now]]+1),now=rc[now];
	}
}
int main()
{
	srand(time(NULL)); //论随机化种子的重要性
	t=in();
	while(t--)
	{
		opt=in(),v=in();
		if(opt==1)
		{
			split(root,v,x,y);
			root=make(make(x,getnew(v)),y);
		}
		else if(opt==2)
		{
			split(root,v,x,z);
			split(x,v-1,x,y);
			y=make(lc[y],rc[y]);
			root=make(make(x,y),z);
		}
		else if(opt==3)
		{
			split(root,v-1,x,y);
			put(f[x]+1);
			putchar(10);
			root=make(x,y);
		}
		else if(opt==4) put(val[find(root,v)]),putchar(10);
		else if(opt==5)
		{
			split(root,v-1,x,y);
			put(val[find(x,f[x])]);
			root=make(x,y);
			putchar(10); 
		}
		else 
		{
			split(root,v,x,y);
			put(val[find(y,1)]);
			root=make(x,y);
			putchar(10); 
		}
	}
	return 0;
}