特征工程：PCA主成分分析（实例）

1.特征转换的介绍

样本特征只能从原始数据集中选择吗?
答案是否定的。
我们可以对原有特征进行组合，转化和提取获取新的特征。
其实生活中有很多这样的例子比如：
从三维空间到二维平面
->用单个摄像头捕获数据时,就像把数据集压入一个二维空间:[x, y, z] ->[CI,C2]
->在特征转换中，一开始就不认为原始特征空间是最好的。
->可能用更少的特征可以更好的描述数据。

下面介绍几个概念：（维度缩减）
特征转换、特征选择

特征选择仅限于从原始列中选择特征;
特征转换算法则将原始列组合起来，从而创建可以更好的特征。
特征选择的降维原理是隔离信号列和忽略噪声列。
特征转换是使用原始数据集建新的列,生成一个全新的数据集。

2.主成分分析（PCA）介绍

PCA是无监督的分类器

主成分分析(PCA,principal components analysis)
将高维数据投影至低维空间，低维空间中的新特征叫主成分/超级列。
只需要几个主成分就可以准确解释整个数据集。

以鸢尾花的数据特征转换为例
矩阵相乘（线性代数里面的知识）
中间的这个4*2的矩阵是怎么来的就是PCA要做的工作
工作流程
1.创建数据集的协方差矩阵;
2.计算协方差矩阵的特征值;
3.保留前n个特征值&特征向量(按特征值降序排列);
4.用保留的特征向量转换新的数据点。

3.PCA工作流程实现

导入数据

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
X, y = load_iris(return_X_y=True)

查看一下当前特征散点图

plt.scatter(X[:,0], X[:, 1],c=y)
plt.grid() 

可以看出在前两个特征的维度上，样本的划分并不是特别的明显。
接下来开始pca的处理
首先对四列特征进行协方差的计算，会得到一个4*4的矩阵

cov_mat = np.cov(X.T)   
cov_mat

在numpy中会把一行看作一个向量，所以先对原始数据进行转置。求得的结果就是4*4的矩阵，对角线的值就是方差，自己和自己的协方差就是方差。
接下来求解特征值和特征向量

eig_val_cov,eig_vec_cov = np.linalg.eig(cov_mat)  # 特征值，特征向量

取前两个特征向量

vec = eig_vec_cov[:,:2]
vec

矩阵相乘，进行特征转化

X_new = np.dot(X, vec)  # 矩阵相乘
X_new.shape

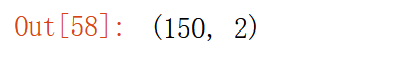
数据就由（150，4）转化成（150，2）
绘制原来数据的散点图和经过特征转换后的散点图

plt.scatter(X[:,0], X[:, 1],c=y)
plt.grid()  
plt.figure() # 创建新的画布
plt.scatter(X_new[:,0], X_new[:, 1],c=y)
plt.grid()

可以看出经过主成分分析后，样品的类别区分的比较明显。可能有一部分必须好奇的读者想知道为什么计算协方差矩阵的特征值和特征向量可以进行特征的转换，其实这里面涉及比较复杂的数学证明，这篇文章主要讲解怎么使用没有公式原理的推理，感兴趣的可以用google学术自行查找。

4.PCA方差分析

细心的可能发现上面数据原始特征有四个，而X[:,0], X[:, 1]只使用了两个特征，而并不能说明原始特征中的其他两个特征不能将数据区分开来，所以我们不能说原始数据的类别不好区分。我们可能还有一个疑问，看起来新的特征X_new区分类别效果较好，但是我们能否确定新的特征包含了原始特征的所有信息呢？所以接下来我们将对这个问题展开讨论。

首先我们将四列数据压缩成两个是肯定有数据信息的丢失
首先看一下四个特征值

eig_val_cov

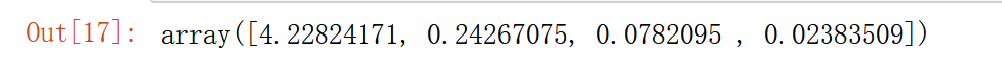算一下占比

eig_val_cov/eig_val_cov.sum()

画碎石图看一下随着特征向量的增多，信息的占比会发生什么情况。

x=eig_val_cov/eig_val_cov.sum()
plt.plot(range(1,5),np.cumsum(x))
plt.grid()

5.利用sklearn实现PCA

获取主成分（超极列）

from sklearn.decomposition import PCA
pca=PCA(n_components=2)           # n_components主成分的个数
X_new_sk=pca.fit_transform(X)     
pca.components_     # 查看特征向量

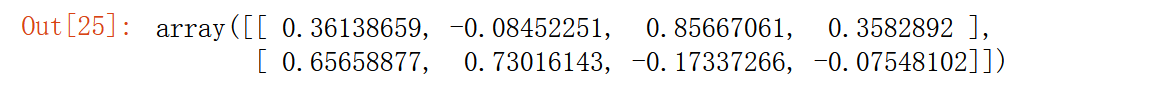画图

plt.scatter(X[:,0], X[:, 1],c=y)
plt.grid()  
plt.figure() # 创建新的画布
plt.scatter(X_new_sk[:,0], X_new_sk[:, 1],c=y)
plt.grid()

我们可以看出使用sklearn画的图y轴的取值范围不同，这是因为使用sklearn中的pca.fit_transform(X) 中增加了对数据中心化操作

6.深入解释PCA之相关性探究

6.1相关特征探究

很多机器学习模型会假设输入的特征是互相独立的,所以消除相关特征好处很大。
PCA中所有主成分都互相垂直，意思是彼此线性无关。

原始特征间的相关性:np.corrcoef(iris_X.T)
主成分/超级列间的相关性:np.corrcoef(pca_iris.T)

机器学习中特征之间彼此并不是完全独立的，比如一个人是否是男性，他有没有胡须和有没有喉结这两个特征就是相关的。特征之间往往是不独立的，而这种不独立性会严重影响模型的性能。

先看一下原始数据的相关性

np.corrcoef(X.T)

我们再看一下超级列的相关性

np.corrcoef(X_new.T)

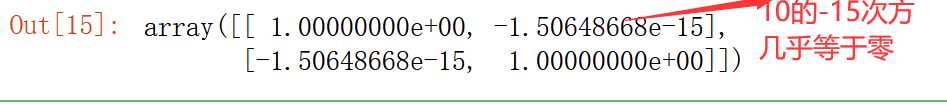
6.2中心化和缩放对PCA的影响

数据中心化（iris_X-mean_vector）不影响特征向量
因为原始矩阵和中心化后矩阵的协方差矩阵相同
注意
在特征工程或机器学习中,特征缩放一般来说都是好的。
在实践和生产环境下建议进行缩放，但需进行性能对比。

7.深入解释PCA之线性变换

矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。先看下面的例子

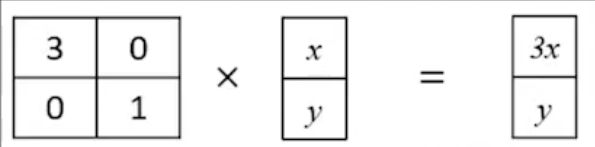
再看一个例子


再看一个从二维到一维的例子


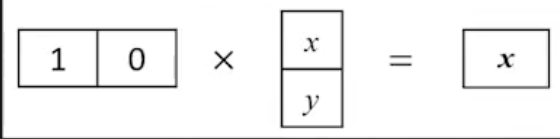
其实主成分分析做的就是线性代数里的线性变换

8.深入解释PCA之数据分布探索

截断iris原始数据，只保留后两个原始特征

PCA转换

原始坐标系中的主成分

新空间中数据及主成分分布

下面看代码

data_2=X[:,2:4]
data_2=data_2-data_2.mean(axis=0)  # 减每一列的均值，中心化操作
pca=PCA(n_components=2) 
X_2_transform=pca.fit_transform(data_2)

def draw_vector(v0, v1, ax):   # 自定义绘制箭头的函数
    arrow_props = dict(arrowstyle='->', linewidth=2, shrinkA=0, shrinkB=0)
    ax.annotate('', v1, v0, arrowprops=arrow_props)

fig, ax = plt.subplots(2, 1, figsize=(10, 10))                              # 创建画布
fig.subplots_adjust(left=0.1, right=0.95, wspace=0.1, hspace=0.25)          # 画布设置
ax[0].scatter(data_2[:, 0], data_2[:, 1], alpha=0.2,c=y)                # 原始空间中的数据点分布
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * np.sqrt(length)                                            # 拉长向量，和explained_variance对应
    draw_vector(pca.mean_, pca.mean_ + v, ax=ax[0])         # 画主成分箭头
ax[0].set(xlabel='x', ylabel='y', title='Original Iris Dataset')

ax[1].scatter(X_2_transform[:, 0], X_2_transform[:, 1], alpha=0.2,c=y)   # 转化后空间中的数据点分布
for length, vector in zip(pca.explained_variance_, pca.components_):
    transformed_component = pca.transform([vector])[0]                         # 将特征向量转换到新坐标空间
    v = transformed_component * np.sqrt(length)                                        # 拉长向量，和explained_variance对应
    draw_vector(X_2_transform.mean(axis=0), X_2_transform.mean(axis=0) + v, ax=ax[1])
ax[1].set(xlabel='component 1', ylabel='component 2', xlim=(-3, 3), ylim=(-1, 1), title='Projected Data')

可以看出，pca处理后特征向量相互垂直且方差大的方向是沿着数据的分布方向。其实pca就是靠放大方差来区分类别

9.PCA总结

深入解释主成分:线性变换
1．原始坐标系的特征向量不是垂直的，指向数据自然遵循的方向
2．新坐标系中的特征向量相互垂直，也就是新的x轴和y轴。
3. PCA是一种特征转换工具，以原始特征的线性组合构建出全新的超级特征。
4. 主成分会产生新的特征，最大化数据的方差，并按方差大小来排序。

对于机器学习来说，方差越大蕴含的信息量越大，如果某一列方差为0，那说明样本的取值都是一样的，方差的定义是一个离散度的标准，方差为0说明所有的样本取值都相同，那对分类没有意义。