对拍找错
#include<bits/stdc++.h>
using namespace std;
int main()
{
int tt = 1;
cin >> tt;
for(int i = 1; i <= tt; i ++){
cout << "Case : " << i << ' ';
system("rand.exe > try.txt");//rand生成数据,try是存放数据文件
system("accode.exe < try.txt > yh.txt");//代码1运行
system("wacode.exe < try.txt > bl.txt");//代码2运行
if(!(system("fc yh.txt bl.txt"))) //输出比较
cout << "yes" << endl;
else break;
}
return 0;
}
交互题
交互题用`fflush(stdout);`刷新缓冲区
KMP
for(int i = 2, j = 0; i <= ns; i ++)//ns为s串长度
{
while(j && s[i] != s[j + 1])
j = nex[j];
if(s[i] == s[j + 1])
j ++;
nex[i] = j;
}
int num = 0;
for(int i = 1, j = 0; i <= nt; i ++)//nt为t串长度
{
while(j && t[i] != s[j + 1])
j = nex[j];
if(t[i] == s[j + 1])
j ++;
if(j == ns)//匹配成功
{
num ++;//num的值为s串在t中出现次数
j = nex[j];
}
}
高斯消元-解线性方程组
#include <iostream>
using namespace std;
const int N = 15;
double a[N][N], b[N][N];
int n;
void gauss()
{
// 转化为上三角矩阵
for(int i = 1; i <= n; i ++)//i表示处理第i列
{
int t = i;//找到最优的某一行来处理这一列
for(int j = i + 1; j <= n; j ++)
if(abs(b[j][i]) > abs(b[t][i]))
t = j;
// 交换
for(int j = i; j <= n + 1; j ++)//把第t行交换到第i行
swap(b[t][j], b[i][j]);
for(int j = n + 1; j >= i; j --)//把第i行同时除以第i行第i列的值
b[i][j] = b[i][j] / b[i][i];
// 消元
for(int j = i + 1; j <= n; j ++)
for(int k = n + 1; k >= i; k --)
b[j][k] = b[j][k] - b[i][k] * b[j][i];
}
// 转化成对角矩阵
for(int i = n; i > 1; i --)
for(int j = i - 1; j >= 1; j --)
{
b[j][n + 1] = b[j][n + 1] - b[j][i] * b[i][n + 1];
b[j][i] = 0;
}
}
int main()
{
cin >> n;
// 输入n + 1个n维方程
for(int i = 0; i <= n; i ++)
for(int j = 1; j <= n; j ++)
cin >> a[i][j];
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
{
b[i][j] = 2 * (a[i][j] - a[0][j]);
b[i][n + 1] += a[i][j] * a[i][j] - a[0][j] * a[0][j];
}
gauss();
for(int i = 1; i <= n; i ++)
printf("%.3lf ", b[i][n + 1]);
}
组合数
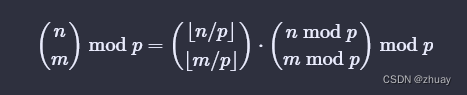
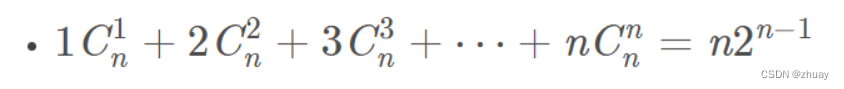
一些组合数公式
欧拉定理
扩展欧拉定理
分解质因数欧拉函数
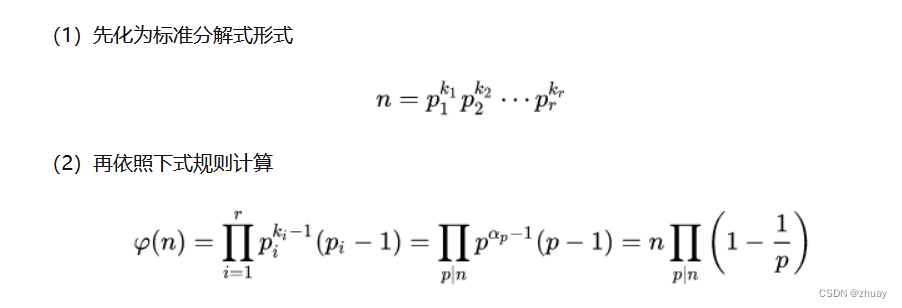代码
int getoula(int n)
{
int res = 1;
for(int i = 2; i * i <= n; i ++)
{
if(n % i == 0)
{
int t = 1;
while(n % i == 0){
n /= i;
t = t * i;
}
t = t / i;
res = res * t * (i - 1);
}
}
if(n > 1)
res = res * (n - 1);
return res;
}
筛法求欧拉函数
int prime[N], st[N], cnt, oula[N];
void getoula(int n)
{
oula[1] = 1;
for(int i = 2; i <= n; i++)
{
if(!st[i])
{
prime[cnt++] = i;
oula[i] = i - 1;
}
for(int j = 0; prime[j] * i <= n; j ++)
{
st[prime[j] * i] = 1;
if(i%prime[j] == 0)
{
oula[prime[j] * i] = oula[i] * prime[j];
break;
}
oula[prime[j] * i] = oula[i] * (prime[j] - 1);
}
}
}
欧拉图、欧拉回路、欧拉路径(通路)
tarjan缩点
void tarjan(int x)
{
dfn[x] = low[x] = ++timetamp;
q.push(x); st[x] = 1;
for(int i = h[x]; i != -1; i = ne[i])
{
if(!dfn[e[i]])
{
tarjan(e[i]);
low[x] = min(low[x], low[e[i]]);
}
else if(st[e[i]] == 1)
low[x] = min(low[x], dfn[e[i]]);
}
if(dfn[x] == low[x])//缩成一个点
{
++ cnt;
while(q.top() != x)
{
id[q.top()] = cnt;//id数组为每个点缩点后在哪个点内
st[q.top()] = 0;
q.pop();
num[cnt] ++;//num为缩后的点由几个原来的点组成
}
id[q.top()] = cnt;
st[q.top()] = 0;
q.pop();
num[cnt] ++;
}
}
int main()
{
cin >> n >> m;
int a, b, res = 0;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i ++)
{
cin >> a >> b;
add(a, b);
}
for(int i = 1; i <= n; i ++)
if(!dfn[i])
tarjan(i);
//缩完点后用新生成的点建边即可建成新的拓扑图
for(int i = 1; i <= n; i ++)
{
for(int j = h1[i]; j != -1; j = ne[j])
{
if(id[i] != id[e[j]])
{
addid(id[i], id[e[j]]);
}
}
}
}
最少的需要新建多少道路，使每两点之间都会至少有两条相互分离的路径，两条路径相互分离，是指两条路径没有一条重合的道路。
#include <iostream>
#include <stack>
#include <cstring>
using namespace std;
const int N = 5020, M = 20020;
int h[N], e[M], ne[M], idx;
int id[N], cnt, d[N];
int dfn[N], low[N], timetamp;
stack<int> q;
void add(int x, int y)
{
e[idx] = y; ne[idx] = h[x]; h[x] = idx ++;
}
void tarjan(int x, int f)
{
dfn[x] = low[x] = ++ timetamp;
q.push(x);
for(int i = h[x]; i != -1; i = ne[i])
{
if(!dfn[e[i]])
{
tarjan(e[i], i);
low[x] = min(low[x], low[e[i]]);
}
else if (i != (f ^ 1))
low[x] = min(low[x], dfn[e[i]]);
}
if(dfn[x] == low[x])
{
int y;
++ cnt;
do{
y = q.top();
q.pop();
id[y] = cnt;
}while(y != x);
}
}
int main()
{
int n, m, a, b;
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i ++)
{
cin >> a >> b;
add(a, b); add(b, a);
}
tarjan(1, -1);
for(int i = 1; i <= n; i ++)
{
for(int j = h[i]; j != -1; j = ne[j])
{
if(id[i] != id[e[j]])
{
d[id[i]] ++;
}
}
}
int ans = 0;
for(int i = 1; i <= cnt; i ++)
{
if(d[i] == 1)
ans ++;
}
cout << (ans + 1) / 2;
}
给定一个由 n 个点 m 条边构成的无向图，请你求出该图删除一个点之后，连通块最多有多少。
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10020, M = 30020;
int h[N], e[M], ne[M], idx, ans, sum;
int dfn[N], low[N], timetamp, root;
void add(int x, int y)
{
e[idx] = y; ne[idx] = h[x]; h[x] = idx ++;
}
void tarjan(int x, int f)
{
int cnt = 0;
dfn[x] = low[x] = ++ timetamp;
for(int i = h[x]; i != -1; i = ne[i])
{
// if((1 ^ f) == i)
// continue;
if(!dfn[e[i]])
{
tarjan(e[i], i);
low[x] = min(low[x], low[e[i]]);
if(low[e[i]] >= dfn[x])
cnt ++;
}
else
low[x] = min(low[x], dfn[e[i]]);
}
if(x != root && cnt)
cnt ++;
ans = max(ans, cnt);
}
int main()
{
int n, m;
while(cin >> n >> m, n)
{
memset(h, -1, sizeof h);
memset(dfn, 0, sizeof dfn);
idx = timetamp = sum = ans = 0;
int a, b;
for(int i = 0; i < m; i ++)
{
cin >> a >> b;
add(a, b); add(b, a);
}
for(int i = 0; i < n; i ++)
{
if(!dfn[i])
{
root = i;
tarjan(i, -1);
sum ++;
}
}
cout << sum + ans - 1 << endl;
}
}
扩展欧几里得
#include <iostream>
#define int long long
using namespace std;
void exgcd(int a, int b, int &x, int &y)
{
if(b == 0)
{
x = 1;
y = 0;
return;
}
exgcd(b, a % b, x, y);
swap(x, y);
y = y - x * (a / b);
}
signed main()
{
int a, b, x, y;
cin >> a >> b;
exgcd(a, b, x, y);
cout << (x % b + b) % b;
}
代码功能是求出最小的正整数x使存在y满足 ax + by = 1.
#include <iostream>
#include <algorithm>
#define int long long
using namespace std;
int d;
int exgcd(int a, int b, int &x, int &y)
{
if(b == 0)
{
if(a == 0 || d % a != 0)
return true;
x = d / a;
y = 0;
return false;
}
if(exgcd(b, a % b, x, y))
return true;
swap(x, y);
y = y - x * (a / b);
return false;
}
signed main()
{
int a, b, x, y, m;
m = b / __gcd(a, b);
exgcd(a, b, x, y);
if(!f)
cout << (x % m + m) % m;
}
改进后能求出最小的正整数x使存在y满足 ax + by = d.
求逆元
逆元可以看作模运算中的倒数，假设 a 模 P 的逆元为 x，则 ax % P = 1（等价于 ax ≡ 1 (% P) )，
x ≡ (1 / a)(% P)，因此(b / a) % P = (b * (1 / a)) % P = (b * x) % P;
1、当 a % P 中的 P 为质数时可以用 费马小定理 求 a 模 P 的逆元，逆元为 a 的 P - 2 次方；
2、如果 P 不是素数，且 a 与 P 互质，则需要用 扩展欧几里得 算法求逆元，调用扩展欧几里得的 exgcd(a, P, x, y); 函数，可以求出满足条件的 x 和 y 使 ax + Py = 1,其中 x 就是 a 模 P 的逆元；
3、如果 a 与 P 不互质则逆元不存在。
中国剩余定理
求x的值为多少，使下面的同余方程都成立
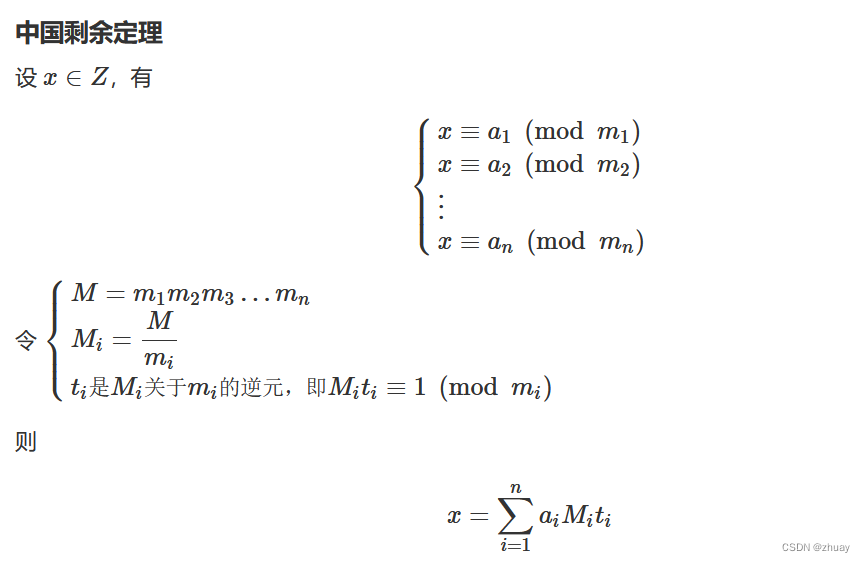x即为这一组同余方程的解，假设 g 为m1，m2，…，mn 的最小公倍数，x + kg(k ∈ Z)则为这组同余方程的所有解
LCA
int h[N], e[N * 2], ne[N * 2], idx, l[N][20], st[N], depth[N];
void add(int x, int y)
{
e[idx] = y; ne[idx] = h[x]; h[x] = idx ++;
}
void dfs(int r)
{
queue<int> q;
q.push(r);
st[r] = 1;
depth[r] = 1;
while(!q.empty())
{
int x = q.front();
q.pop();
for(int i = h[x]; i != -1; i = ne[i])
if(!st[e[i]])
{
q.push(e[i]);
depth[e[i]] = depth[x] + 1;
st[e[i]] = 1;
l[e[i]][0] = x;
for(int j = 1; j < 20; j ++)
l[e[i]][j] = l[l[e[i]][j - 1]][j - 1];
}
}
}
int lca(int x, int y)
{
if(depth[x] < depth[y])
swap(x, y);
for(int i = 19; i >= 0; i --)
if(depth[l[x][i]] >= depth[y])
x = l[x][i];
if(x == y)
return x;
for(int i = 19; i >= 0; i --)
{
if(l[x][i] != l[y][i])
{
x = l[x][i]; y = l[y][i];
}
}
return l[x][0];
}
中国剩余定理
网络流
求最大流，且图的最小割在数值上等于最大流
最大流：给出一个包含 n 个点和 m 条边的有向图（称其为网络），该网络上所有点分别编号为 1∼n，所有边分别编号为 1∼m，其中该网络的源点为 s，汇点为 t，网络上的每条边 (u,v) 都有一个流量限制 c(u,v)，你需要给每条边 (u,v) 确定一个流量 f(u,v)，要求除了源点和汇点外，其他各点流入的流量和流出的流量相等，源点流出的流量等于汇点流入的流量，最大流的值即为源点单位时间流出或汇点流入的流量.
Edmonds-Karp算法，复杂度nm^2, n表示点数，m表示边数,默认添加无向边,下面还有两个优化后的最大流算法
#include <iostream>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
const int N = 10000, S = 1e15;
int h[N], ne[N], e[N], w[N], idx;
int s, t, ans = 0;
int st[N], pre[N], dist[N];
void add(int x, int y, int z)
{
e[idx] = y;
ne[idx] = h[x];
w[idx] = z;
h[x] = idx ++;
}
void flow(int x, int f)
{
if(pre[x] != -1)
{
w[pre[x] ^ 1] -= f;
w[pre[x]] += f;
flow(e[pre[x]], f);
}
else
ans = ans + f;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int n, m, a, b, c, x;
cin >> n >> m >> s >> t;
memset(h, -1, sizeof h);
while(m --){
cin >> a >> b >> c;
add(a, b, c);
add(b, a, 0);
}
while(1){
queue<int> q;
q.push(s);
dist[s] = S;
for(int i = 1; i <= n; i ++)
pre[i] = -1;
while(!q.empty()){
x = q.front();
q.pop();
for(int i = h[x]; i != -1; i = ne[i])
{
if(e[i] != s && pre[e[i]] == -1 && w[i] > 0)
{
pre[e[i]] = i ^ 1;
dist[e[i]] = min(dist[x], w[i]);
q.push(e[i]);
}
}
if(pre[t] != -1)
break;
}
if(pre[t] != -1)
flow(t, dist[t]);
else
break;
}
cout << ans << '\n';
}
Dinic算法,优化后的最大流算法，复杂度为n^2m,同样加无向边,下面还有再次优化的Dinic算法
#include <iostream>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
const int N = 10000, S = 1e15;
int h[N], ne[N], e[N], w[N], idx;
int n, s, t, ans = 0;
int dist[N], deep[N];
void add(int x, int y, int z)
{
e[idx] = y;
ne[idx] = h[x];
w[idx] = z;
h[x] = idx ++;
}
int dfs(int u, int s)
{
if(u == t)
return s;
int x;
for(int i = h[u]; i != -1; i = ne[i])
{
if(deep[e[i]] == deep[u] + 1 && w[i] != 0)
{
x = dfs(e[i], min(s, w[i]));
if(x)
{
w[i] -= x;
w[i ^ 1] += x;
return x;
}
else
deep[e[i]] = -1;
}
}
return 0;
}
int bfs()
{
queue<int> q;
int x;
q.push(s);
for(int i = 1; i <= n; i ++)
{
deep[i] = -1;
}
deep[s] = 1;
while(!q.empty()){
x = q.front();
q.pop();
for(int i = h[x]; i != -1; i = ne[i])
{
if(deep[e[i]] == -1 && w[i] > 0)
{
deep[e[i]] = deep[x] + 1;
q.push(e[i]);
if(e[i] == t)
return 1;
}
}
}
if(deep[t] == -1)
return 0;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int m, a, b, c, x;
cin >> n >> m >> s >> t;
memset(h, -1, sizeof h);
while(m --){
cin >> a >> b >> c;
add(a, b, c);
add(b, a, 0);
}
while(bfs()){
while(x = dfs(s, S)){
ans += x;
}
}
cout << ans << '\n';
}
下面是head数组优化的Dinic算法,改动了两处
1、在dfs循环中定义循环变量 i 时加了 & 符号
2、在bfs初始化中将 head[i] 初始化为 h[i]
#include <iostream>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
const int N = 10000, S = 1e15;
int h[N], ne[N], e[N], w[N], idx, head[N];
int n, s, t, ans = 0;
int dist[N], deep[N];
void add(int x, int y, int z)
{
e[idx] = y;
ne[idx] = h[x];
w[idx] = z;
h[x] = idx ++;
}
int dfs(int u, int s)
{
if(u == t)
return s;
int x;
for(int& i = head[u]; i != -1; i = ne[i])//此处多了&符号，也可此处不加&符号而在下面加代码head[u] = i;
{
if(deep[e[i]] == deep[u] + 1 && w[i] != 0)
{
x = dfs(e[i], min(s, w[i]));
if(x)
{
w[i] -= x;
w[i ^ 1] += x;
return x;
}
else
deep[e[i]] = -1;
}
}
return 0;
}
int bfs()
{
queue<int> q;
int x;
q.push(s);
for(int i = 1; i <= n; i ++)
{
deep[i] = -1;
head[i] = h[i];
}
deep[s] = 1;
while(!q.empty()){
x = q.front();
q.pop();
for(int i = h[x]; i != -1; i = ne[i])
{
if(deep[e[i]] == -1 && w[i] > 0)
{
deep[e[i]] = deep[x] + 1;
q.push(e[i]);
if(e[i] == t)
return 1;
}
}
}
if(deep[t] == -1)
return 0;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int m, a, b, c, x;
cin >> n >> m >> s >> t;
memset(h, -1, sizeof h);
while(m --){
cin >> a >> b >> c;
add(a, b, c);
add(b, a, 0);
}
while(bfs()){
while(x = dfs(s, S)){
ans += x;
}
}
cout << ans << '\n';
}
费用流
添加条件，网络上每条边都要花费，要求在保证最大流最大的情况下花费最小,这里每条边的花费是按这条边用到的容量在计算的
直接spfa求解，会比Dijkstra慢，下面有Dijkstra代码
#include <iostream>
#include <cstring>
#include <queue>
#define int long long
using namespace std;
const int N = 100000, S = 1e15;
int h[N], ne[N], e[N], w[N], f[N], idx, head[N];
int n, s, t, ans, sum;
int dist[N], cost[N], pre[N], st[N];//dist数组存的是从起点到当前点的最大流量，cost数组存的是起点到当前点每单位容量的花费，st数组用来执行spfa
void add(int x, int y, int z, int c)
{
e[idx] = y;
ne[idx] = h[x];
w[idx] = z;
f[idx] = c;
h[x] = idx ++;
}
int spfa()
{
for(int i = 1; i <= n; i ++)
{
st[i] = 0;
pre[i] = -1;
cost[i] = 1e15;
}
queue<int> q;
q.push(s);
st[s] = 1;
dist[s] = S;
cost[s] = 0;
int x;
while(!q.empty()){
x = q.front();
q.pop();
st[x] = 0;
for(int i = h[x]; i != -1; i = ne[i])
{
if(w[i] > 0 && cost[x] + f[i] < cost[e[i]])//这里比较的是单位容量的花费
{
dist[e[i]] = min(dist[x], w[i]);
cost[e[i]] = cost[x] + f[i];
pre[e[i]] = i ^ 1;
if(!st[e[i]])
{
q.push(e[i]);
st[e[i]] = 1;
}
}
}
}
return pre[t] != -1;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int m, a, b, c, x;
cin >> n >> m >> s >> t;
memset(h, -1, sizeof h);
while(m --){
cin >> a >> b >> c >> x;//输入有向边的起点、终点，最大容量和单位容量的花费
add(a, b, c, x);
add(b, a, 0, -1 * x);
}
while(spfa()){
ans += dist[t];
sum += dist[t] * cost[t];
x = t;
while(x != s){
w[pre[x]] += dist[t];
w[pre[x] ^ 1] -= dist[t];
x = e[pre[x]];
}
}
cout << ans << ' ' << sum << '\n';
}
原始对偶算法
这个算法没学，只把板子粘了过来
因为有负边所以不能用单纯的Dijkstra，要使用 Dijkstra 并优化复杂度需要保证没有负权环，要想办法把每条边的边权变为非负数，原始对偶算法就是这样一个方法，它给每个点增加了一个“势能”，利用势能和边权来把边权全部变为非负数
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+5,M=1e5+5,INF=2e9;
int n,m,s,t;
int maxflow=0,mincost=0;
int head[N],fr[M],nxt[M],to[M],cnt=1;
int cap[M],w[M],fl[M],v[M],h[N]/*势能*/,dis[N];
int pre[N];
bool vis[N];
inline void create(int ff,int tt,int cc,int ww){nxt[++cnt]=head[ff],fr[cnt]=ff,head[ff]=cnt,to[cnt]=tt,cap[cnt]=cc,w[cnt]=ww;}
void spfa()//SPFA算初始势能
{
static queue<int>q;
for(int i=1;i<=n;++i)h[i]=INF;
h[s]=0,vis[s]=1;
q.push(s);
int tmp;
while(q.size())
{
tmp=q.front();
q.pop();
vis[tmp]=0;
for(int i=head[tmp];i;i=nxt[i])
{
if(cap[i]&&h[to[i]]>h[tmp]+w[i])
{
h[to[i]]=h[tmp]+w[i];
if(!vis[to[i]]) vis[to[i]]=1,q.push(to[i]);
}
}
}
}
bool dij()//找增广路
{
typedef pair<int,int> pii;
static priority_queue<pii,vector<pii>,greater<pii>>q;
for(int i=1;i<=n;++i)dis[i]=INF,vis[i]=0;
dis[s]=0;
q.push(make_pair(0,s));
int tmp;
while(!q.empty())
{
tmp=q.top().second;
q.pop();
if(vis[tmp])continue;
vis[tmp]=1;
for(int i=head[tmp],neww;i;i=nxt[i])
{
neww=w[i]+h[tmp]-h[to[i]];//更新边权
if(cap[i]>fl[i]&&dis[to[i]]>dis[tmp]+neww)
{
dis[to[i]]=dis[tmp]+neww;
pre[to[i]]=i;
if(!vis[to[i]])q.push(make_pair(dis[to[i]],to[i]));
}
}
}
return dis[t]!=INF;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>s>>t;
for(int i=1,t1,t2,t3,t4;i<=m;++i)cin>>t1>>t2>>t3>>t4,create(t1,t2,t3,t4),create(t2,t1,0,-t4);
spfa();
while(dij())
{
int flow=INF;
for(int i=t;i!=s;i=fr[pre[i]])flow=min(flow,cap[pre[i]]-fl[pre[i]]);//回溯
for(int i=t;i!=s;i=fr[pre[i]])
{
fl[pre[i]]+=flow;
fl[pre[i]^1]-=flow;
}
maxflow+=flow;
mincost+=flow*(h[t]+dis[t]);
for(int i=1;i<=n;++i)h[i]+=dis[i];
}
cout<<maxflow<<' '<<mincost;
return 0;
}
1069
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
