算法基础复盘笔记Day07【搜索与图论】—— Prim、Kruskal、染色体判定二分图、匈牙利算法

最新推荐文章于 2023-06-03 16:15:06 发布

Java技术一点通

最新推荐文章于 2023-06-03 16:15:06 发布

阅读量1.4k

点赞数 1

分类专栏：数据结构与算法文章标签： Prim Kruskal 染色法判定二分图匈牙利算法

本文链接：https://blog.csdn.net/m0_52691962/article/details/128379092

版权

数据结构与算法专栏收录该内容

12 篇文章 4 订阅

订阅专栏

❤ 作者主页：欢迎来到我的技术博客😎
❀ 个人介绍：大家好，本人热衷于Java后端开发，欢迎来交流学习哦！(￣▽￣)~*
🍊 如果文章对您有帮助，记得关注、点赞、收藏、评论⭐️⭐️⭐️
📣 您的支持将是我创作的动力，让我们一起加油进步吧！！！🎉🎉

第一章 Prim

一、Prim算法求最小生成树

1. 题目描述

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 $G = (V, E)$ ，其中 V 表示图中点的集合，E 表示图中边的集合， $n = ∣ V ∣$ ， $m = ∣ E ∣$ 。

由 V 中的全部 n 个顶点和 E 中 $n - 1$ 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 $u, v, w$ ，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

$1≤n≤500,
$KaTeX parse error: Expected group after '^' at position 8: 1\leqm\leq105^̲$ ,
图中涉及边的边权的绝对值均不超过 10000。

输入样例：

输出样例：

2. 思路分析

算法流程与 Dijkstra算法相似：

初始化，将所有点的 $d i s t$ 设为正无穷，第一个点的 $d i s t$ 值为0，这里的 $d i s t$ 数组是存储点到集合的距离；
每次选择距离当前集合距离最短的点，如果该点与集合不连通，表示不存在生成树，则直接 INF，否则，更新权值和 $res$ ，并将该点加入集合中；
对所有的邻点的距离进行更新操作；
重复操作2、3，进行 $n$ 次迭代。

Prim算法与Dijkstra算法的区别：

Dijkstra 算法是更新不在集合中的点离 起点 的距离: dist[j]=min(dist[j], dist[t]+g[t][j])
Prim 是更新不在集合中的点离 集合S 的距离: dist[j] = min(dist[j], g[t][j])

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 520, INF = 0x3f3f3f3f;

int n, m;
int g[N][N]; //邻接矩阵存储所有的边
int dist[N]; //存储点到集合的距离
bool st[N];

int prime()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    int res = 0; //所有边的权值和
    
    for (int i = 0; i < n; i ++)
    {
        int t = -1; //t是用来记录离集合S最近的点到S的距离，t的初始值设置为-1，距离不可能为负，所以第一次就会更新
        for (int j = 1; j <= n; j ++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        //判断是否联通，有无最小生成树
        if (dist[t] == INF) return INF;
       
        res += dist[t]; //更新权重和
        
        st[t] = true; //标记加入集合
        
        //更新其他边
        for (int j = 1; j <= n; j ++)
            dist[j] = min(dist[j], g[t][j]); //由于是点到集合的距离，所以是g[t][j],而不是dist[t]+g[t][j]
    }
    return res;
}

int main()
{
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g); //初始化邻接矩阵
    
    while (m --)
    {
        int a, b, c;
        cin >>  a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    int t = prime();
    
    if (t == INF) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

第二章 Kruskal

一、Kruskal算法求最小生成树

1. 题目描述

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 $G = (V, E)$ ，其中 V 表示图中点的集合，E 表示图中边的集合， $n = ∣ V ∣$ ， $m = ∣ E ∣$ 。

由 V 中的全部 n 个顶点和 E 中 $n - 1$ 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 $u, v, w$ ，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

$1≤n≤10^5,
$1≤m≤2∗10^5,
图中涉及边的边权的绝对值均不超过 1000。

输入样例：

输出样例：

2. 思路分析

初始化并查集，把 n 个点放在 n 个独立的集合；
将所有的边按边权从小到大排序；
按顺序枚举每一条边，如果这条边连接的两个点不在同一个集合，就把这条边加入最小生成树，并且和并这两个集合；如果这条边连接的两个点在同一集合，就跳过；
重复执行步骤3，直到选取了 $n - 1$ 条边为止；

Kruskal图解：
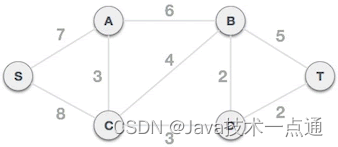
在这里插入图片描述

将连通网中的所有边按照权值大小做升序排序：

B,D D,T A,C C,D C,B B,T A,B S,A S,C
2 2 3 3 4 5 6 7 8
从 B-D 边开始挑选，由于尚未选择任何边组成最小生成树，且 B-D 自身不会构成环路，所以 B-D 边可以组成最小生成树：
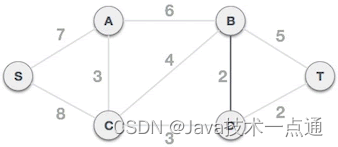
D-T 边不会和已选 B-D 边构成环路，可以组成最小生成树：
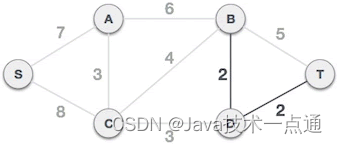
A-C 边不会和已选 B-D、D-T 边构成环路，可以组成最小生成树：
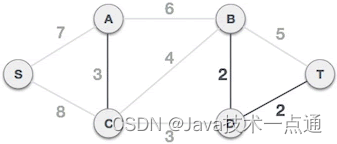
C-D 边不会和已选 A-C、B-D、D-T 边构成环路，可以组成最小生成树：
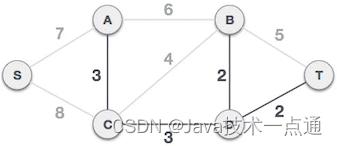
C-B 边会和已选 C-D、B-D 边构成环路，因此不能组成最小生成树：
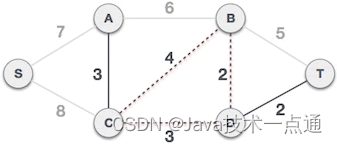
B-T 、A-B、S-A 三条边都会和已选 A-C、C-D、B-D、D-T 构成环路，都不能组成最小生成树。而 S-A 不会和已选边构成环路，可以组成最小生成树：
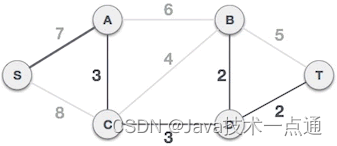
如图下图所示，对于一个包含 6 个顶点的连通网，我们已经选择了 5 条边，这些边组成的生成树就是最小生成树。

B,D	D,T	A,C	C,D	C,B	B,T	A,B	S,A	S,C
2	2	3	3	4	5	6	7	8

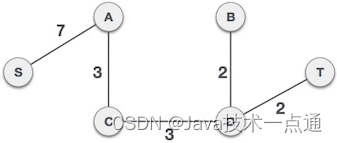
3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge 
{
    int a, b, w;
    //重载小于号，通过边权进行排序
    bool operator<(const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

//并查集
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    //对所有边按边权从小到大排序
    sort(edges, edges + m);
    
    //并查集初始化
    for (int i = 1; i <= n; i ++) p[i] = i;
    
    //res为最小的权重和，cnt为加入最小生成树的边数
    int res = 0, cnt = 0;
    
    for (int i = 0; i < m; i ++) //遍历每一条边
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        
        a = find(a), b= find(b);
        //如果这条边对应的两个点不在同一个集合
        if (a != b)
        {
            p[a] = b;//将a、b加入到同一个集合
            res += w; //更新权重和
            cnt ++; //边数+1
        }
    }
    //加入的边数小于n - 1，则不存在最小生成树
    if (cnt < n - 1) return INF;
    return res;
}

int main()
{
    cin >> n >> m;
    
    for (int i = 0; i < m; i ++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }
    
    int t = kruskal();
    
    if (t == INF) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

第三章染色体判定二分图

一、染色体判定二分图

1. 题目描述

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 u 和 v，表示点 u 和点 v 之间存在一条边。

输出格式

如果给定图是二分图，则输出 Yes，否则输出 No。

数据范围

$1≤n,m≤10^5$

输入样例：

输出样例：

Yes

2. 思路分析

二分图： 如果一张无向图的 $N$ 个节点可以分为 A，B两个不相交的非空集合，并且同一集合内的点之间没有边相连，那么称该无向图为二分图。

定理： 二分图不存在奇环（长度是奇数的环）
因为每一条边都是从一个集合走到另一个集合，只有走偶数次才可能回到同一个集合。

染色法： 我们可以使用染色法来判定二分图。即尝试用两种颜色标记图中的节点，当一个点被标记后，所有与它相邻的节点应该标记与它相反的颜色，若标记过程产生冲突，则说明图中存在奇环，即不存在二分图。可以用 DFS 或 BFS来实现。

算法流程：

color[] 初始化为0，被访问的点的颜色是1或2；
依此遍历搜所有的点，对点进行染色；
枚举点 $u$ 的邻点 $v$ ，如果点 $v$ 未染色，则递归对 $v$ 进行染色，若产生冲突则返回 $f a l se$ ；如果点 $v$ 已经染色且颜色与点 $u$ 相同，则发生冲突，即不存在二分图；
枚举完 $u$ 的所有邻点，如果发生冲突，则表示不存在二分图，否则存在二分图。

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010, M = 200010;

int n, m;
int h[N], e[M], ne[M], idx; //邻接表存储图
int color[N]; //保存各个点的颜色，0是未染色，1是红色，2是绿色

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool dfs(int u, int c)
{
    color[u] = c; //u点染成颜色c
    
    //遍历u相邻的所有点
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        //相邻的点没有染色，则递归处理这个相邻点
        if (!color[j])
        {
            if (!dfs(j, 3 - c)) return false; //（3 - 1 = 2， 如果 u 的颜色是2，则和 u 相邻的染成 1）
                                              //（3 - 2 = 1， 如果 u 的颜色是1，则和 u 相邻的染成 2）
        }
        //如果相邻点已经染色且颜色一样，则发生冲突
        else if (color[j] == c) return false;
    }
    return true;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h); //初始化邻接表
    
    //读入所有边
    while (m --)
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图
    }
    
    bool flag = true;
    for (int i = 1; i <= n; i ++) // 遍历点
        if (!color[i]) //如果没有染色
        { 
            if (!dfs(i, 1)) //对该点进行染色
            {
                flag = false;
                break;
            }
        }
    if (flag) puts("Yes");
    else puts("No");
    
    return 0;
}

第四章匈牙利算法

二分图的最大匹配

1. 题目描述

给定一个二分图，其中左半部包含 $n_1$ 个点（编号 $1∼n_1$ ），右半部包含 $n_2$ 个点（编号 $1∼n_2$ ），二分图共包含 m 条边。

数据保证任意一条边的两个端点都不可能在同一部分中。

请你求出二分图的最大匹配数。

二分图的匹配：给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

输入格式

第一行包含三个整数 $n_1$ 、 $n_2$ 和 m。

接下来 m 行，每行包含两个整数 u 和 v，表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。

输出格式

输出一个整数，表示二分图的最大匹配数。

数据范围

$1≤n_1,n_2≤500$ ,
$1≤u≤n_1$ ,
$1≤v≤n_2$ ,
$1≤m≤10^5$

输入样例：

输出样例：

2. 思路分析

枚举 $n$ 个男生，每轮 st[] 初始化为0（即女生皆可选），深搜若能配成对，则 $res$ 加1；
枚举男生 $u$ 的心仪妹子 $v$
- 若妹子已标记，则跳过；
- 若妹子没男友，则配成对；若妹子的男友可以让出，则配成对；
- 否则，枚举 $u$ 的下一个心仪妹子；
枚举完 $u$ 的所有心仪妹子，如果都保不能配成对，则返回 $f a l se$ 。

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N]; //match[j] = x，表示女孩j的现有配对男友是x
bool st[N];   //st[j] = x，表示一轮匹配模拟中，女孩j被男孩a预定了

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

//这个函数的作用是用来判断，加入x来参与模拟配对，会不会使匹配数增多
bool find(int x)
{
    //遍历自己喜欢的所有女孩
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) //如果在这一轮匹配中，这个女孩还没有被预定
        {
            st[j] = true; //那x就预定这个女孩了 
            //如果女孩j没有男朋友，或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    //自己喜欢的女孩全部被预定了，配对失败
    return false;
}

int main()
{
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    
    while (m --)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    
    int res =0;
    for (int i = 1; i <= n1; i ++)
    {
        //因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
        memset(st, false, sizeof st);
        if (find(i)) res ++;
    }
    cout << res << endl;
    
    return 0;
}

创作不易，如果有帮助到你，请给文章点个赞和收藏，让更多的人看到！！！
关注博主不迷路，内容持续更新中。

Java技术一点通

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
打赏
0
评论
算法基础复盘笔记Day07【搜索与图论】—— Prim、Kruskal、染色体判定二分图、匈牙利算法

二分图：如果一张无向图的 $N$ 个节点可以分为 A，B两个不相交的非空集合，并且同一集合内的点之间没有边相连，那么称该无向图为二分图。定理：二分图不存在奇环（长度是奇数的环）因为每一条边都是从一个集合走到另一个集合，只有走偶数次才可能回到同一个集合。染色法：我们可以使用染色法来判定二分图。即尝试用两种颜色标记图中的节点，当一个点被标记后，所有与它相邻的节点应该标记与它相反的颜色，若标记过程产生冲突，则说明图中存在奇环，即不存在二分图。
复制链接

扫一扫