目录
一、前言
本文主要讲了树状数组的原理及其应用,涉及到了前缀和思想、差分思想。另外,补充另一篇关于树状数组的文章:lowbit和树状数组的理解与部分应用_吕同学的头发不能秃的博客-CSDN博客
二、树状数组的原理
1、杂论
- 树状数组(Binary Indexed Tree, BIT),利用数的二进制特征进行检索的一种树状结构。
- 一种真正的高级数据结构:二分思想、二叉树、位运算、前缀和
- 高效!
- 代码极其简洁!
【基本应用】
数列 a1,a2, ....,an,操作:
(1)修改元素 add(k, x):把ak加上x
(2)求和:sum(x) = a1 + ... +ax
区间和 ai + ... + aj = sum(j) - sum(i-1)
【不修改、只查询】
数列 a1, a2, ..., an,求区间和:ai +...+ aj
- 数列是静态的,用前缀和计算区间和,特别高效。
- 前缀和:sum[i] = a1 + ... + ai
- 区间和:ai + ... + aj = sum[j] - sum[i-1]
- 查询一次区间和,O(1)
a=[0,4,5,6,7,8,9,10,11,12,13]
sum=[0]*20
sum[1]=a[1]
for i in range(2,11): #计算前缀和
sum[i]=sum[i-1]+a[i]
print(sum)
for i in range(1,11): #用前缀和反推计算数组a[]
print(sum[i]-sum[i-1],end=' ')
print("[5,8]=",sum[8]-sum[4]) #查询区间和,例如查询[5,8]【讨论】
如果数列是动态的,修改元素 add(k,x) 把ak加上x,复杂度是O(1);求区间和 sum(j)-sum(i-1),复杂度为O(n),求区间和的效率比较低。
【动态修改、求区间和:用树状数组】
数列是动态的
修改元素 add(k,x):把ak加上x。
求区间和:sum(j)-sum(i-1)
复杂度都是:O(logn)
def lowbit(x):
return x&-x
def add(x,d):
while x<n:
tree[x]+=d
x+=lowbit(x)
def sum(x):
ans=0
while x>0:
ans+=tree[x]
x-=lowbit(x)
return ans2、从二叉树到树状数组
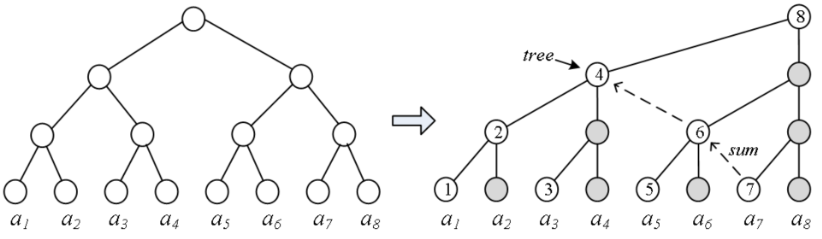
3、神奇的 lowbit(x) 操作
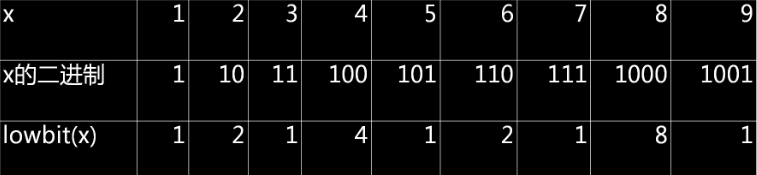
- lowbit(x) = x & -x
- 功能:找到 x 的二进制数的最后一个 1
4、tree[ ]数组:将一维信息转换为树形信息存储
从 lowbit(x) 推出 tree[] 数组,所有的计算都基于 tree[]
令 m = lowbit(x)
定义tree[x]:把 ax 和它前面共 m 个数相加。
例:lowbit(6)=2,有 tree[6]=a5+a6
横线中的黑色表示 tree[x],等于横线上元素相加的和
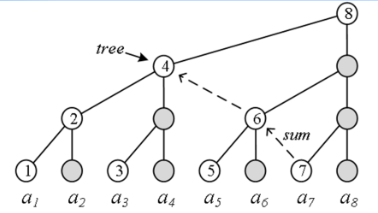
5、基于 tree[ ] 的计算
(1)求和 sum=a1 + ... + ax
利用 tree[] 数组求 sum,例如:
sum[8] = tree[8]
sum[7] = tree[7] + tree[6] + tree[4]
sum[9] = tree[9] + tree[8]
以上关系是如何得到的?借助lowbit(x)
【sum的计算】(要减lowbit)
例:sum[7] = tree[7] + tree[6] + tree[4]
(1)从 7 开始,加上 tree[7];
(2)7-lowbit(7)=6,加上tree[6];
(3)6-lowbit(6)=4,加上tree[4];
(4)4-lowbit(4)=0,结束。
写出数的二进制进行加减你会更加清晰其中的道理,以及为什么要这么设计。
sum() 的复杂度?
O(logn)
非常好!
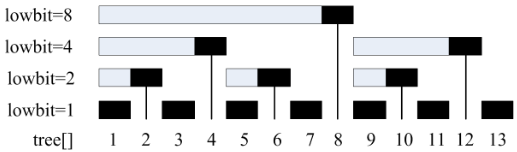
6、tree[]的更新(要加lowbit)
更改 ax,和它相关的 tree 都会变化。
例如改变 a3,那么 tree[3]、 tree[4]、tree[8]... 都会改变。
影响哪些 tree[ ]?仍然利用 lowbit(x):
(1)更改tree[3];
(2)3+lowbit(3)=4,更改 tree[4];
(3)4+lowbit(4)=8,更改 tree[8];
(4)直到最后的 tree[n]。
复杂度?
O(logn)
非常好!
三、树状数组的应用
1、单点修改、区间查询
【题目描述】
数列 a1, a2, ..., ai,操作:
(1)修改元素 add(k, x):把ak加上x。
(2)求和:
sum(x) = a1 +... +ax
区间和 ai + ... + aj = sum(j) - sum(i-1)
【代码】
def lowbit(x):
return x&-x
def add(x,d): #给元素a[x]加上d
while x<=N:
tree[x]+=d
x+=lowbit(x)
def sum(x): #返回前缀和sum
ans=0
while x>0:
ans+=tree[x]
x-=lowbit(x)
return ans
N=1000
tree=[0]*N
a=[0,4,5,6,7,8,9,10,11,12,13]
for i in range(1,11): #计算tree[]数组
add(i,a[i])
print("old:[5,8]=",sum(8)-sum(4)) #查询区间和,例如查询[5,8]
add(5,100) #模拟一次修改:a[5]=a[5]+100
print("new:[5,8]=",sum(8)-sum(4)) 2、区间修改、区间查询(lanqiaoOJ1133)
【题目描述】
给定一个长度为 N 的数组 a,初值为 a1, a2, ..., aN
有 Q 个操作,操作有两种:
1 L R d:将区间 [L,R] 内每个数加上 d。
2 L R:输出区间 [L,R] 内每个数的和。
【输入描述】
第 1 行是整数 N、M,表示数组 a 的长度和操作个数。1<=n, m<=10^5
第 2 行包含 N 个非负整数 a1, a2, ...aN,表示数组 a 的初值
第 3~M+2 行每行表示一个操作
【输出描述】
输出每行一个整数,表示查询的答案
【输入样例】
5 5
1 2 3 4 5
2 1 2
1 2 3 1
2 1 3
1 1 5 1
2 1 5
【输出样例】
3
8
22
【输入处理代码】
n,m=map(int,input().split())
#old=0
a=[0]+[int(i) for i in input().split()] #a[0]不用
for _ in range(m):
g=[int(i) for i in input().split()]
if g[0]==1: #区间修改
L,R,d=g[1],g[2],g[3]
else: #区间询问
L,R=g[1],g[2](1)区间修改:利用差分(差分天然适合区间修改)
一维差分数组 D[k]=a[k]-a[k-1],即原数组 a[] 的相邻元素的差
差分数组能提高修改的效率。
把区间 [L,R] 内每个元素 a[] 加上 d,只需把对应的 D[] 做以下操作:
(1)把 D[L] 加上 d:D[L] += d
(2)把 D[R+1] 减去 d:D[R+1] -= d
利用 D[],能极快解决修改区间 [L,R] 内元素的目的。原来需要 O(n) 次计算,现在只需要O(1)。
说明:前缀和 a[x]=D[1]+D[2]+...+D[x],有:
(1)1<=x<L,前缀和 a[x] 不变;
(2)L<=x<=R,前缀和 a[x] 增加了 d;
(3)R<x<=N,前缀和 a[x] 不变,因为被 D[R+1] 中减去的 d 抵消了。
(2)区间查询(利用差分数组输出区间和)
- 推导区间和,看它和求前缀和有没有关系,如果有关系,就能用树状数组。
- 最后的公式有两个前缀和
- 用两个树状数组分别处理:一个实现 Di,一个实现 (i - 1)Di。
【树状数组初始化】
(1)区间修改 D[k] = a[k] - a[k-1]
(2)区间查询
def lowbit(x):
return x&-x
def update1(x,d): #修改元素a[x],a[x]=a[x]+d
while x<=N:
tree1[x]+=d
x+=lowbit(x)
def update2(x,d):
while x<=N:
tree2[x]+=d
x+=lowbit(x)
def sum1(x):
ans=0
while x>0:
ans+=tree1[x]
x-=lowbit(x)
return ans
def sum2(x):
ans=0
while x>0:
ans+=tree2[x]
x-=lowbit(x)
return ans
N=100010
tree1=[0]*N
tree2=[0]*N #2个差分树状数组
n,m=map(int,input().split())
old=0
a=[0]+[int(i) for i in input().split()] #a[0]不用
for i in range(1,n+1):
update1(i,a[i]-old) #差分数组原理,初始化
update2(i,(i-1)*(a[i]-old))
old=a[i]
for _ in range(m):
g=[int(i) for i in input().split()]
if g[0]==1: #区间修改
L,R,d=g[1],g[2],g[3]
update1(L,d) #第1个树状数组
update1(R+1,-d)
update2(L,d*(L-1)) #第2个树状数组
update2(R+1,-d*R) #d*R=d*(R+1-1)
else: #区间询问
L,R=g[1],g[2]
print(R*sum1(R)-sum2(R)-(L-1)*sum1(L-1)+sum2(L-1))
以上,树状数组的原理和区间和
祝好














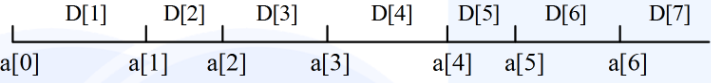

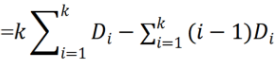















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










