算法设计技巧与分析（七）：回溯(Backtracking)

---

回溯(Backtracking)

• 节点以深度优先搜索方式生成；

• 不需要存储整个搜索树，只需要存储从根节点到当前活动节点的路径。事实上，根本不生成任何物理节点，整棵树都是隐式的。

一、三着色问题(The 3-Coloring Problem)

给定一个无向图G=（V，E），需要用三种颜色中的一种给V中的每个顶点上色，例如1、2和3，这样相邻的两个顶点就没有相同的颜色。我们称这种颜色为合法的；否则，如果两个相邻顶点具有相同的颜色，则为非法的。着色可以用n元组（c1，c2，…，cn）表示，这样ci属于{1, 2, 3}。

所有可能的颜色集都可以用一个称为搜索树的完整三元树来表示。在该树中，从根节点到叶节点的每个路径代表一个着色分配。如果没有两个相邻的着色顶点具有相同的颜色，则图的不完全着色是部分着色。

• 如果此路径的长度小于n且相应的着色为部分着色，则生成当前节点的一个子节点并将其标记为当前节点。

• 如果对应的路径不是部分着色的，则当前节点被标记为死节点，并生成对应于另一种颜色的新节点。

• 如果尝试了所有三种颜色但均未成功，则搜索将返回到颜色已更改的父节点，依此类推。

搜索树的构建如下图所示：

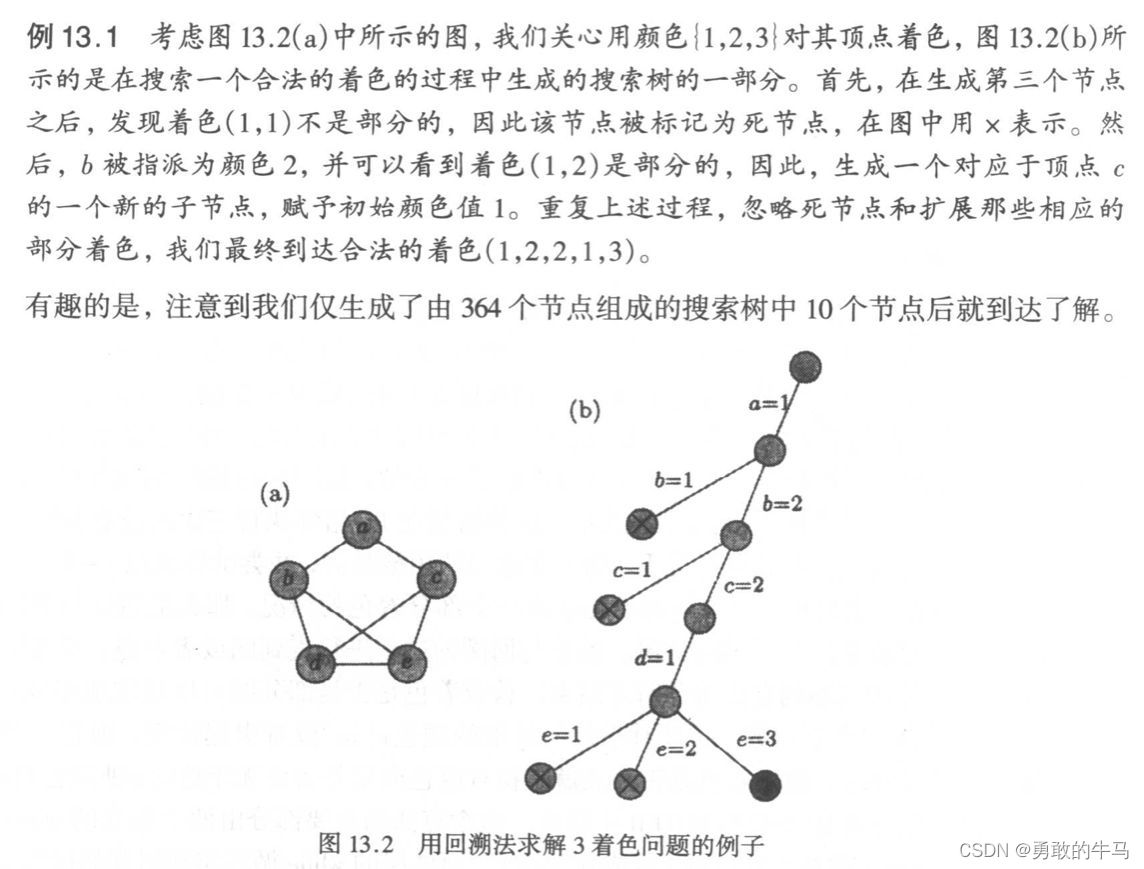
算法伪代码如下：

递归算法：

Input: 无向图G=(V, E).
Output: G的顶点的3-着色c[1…n]，其中每个c[j]是1、2或3。
for k = 1 to n:
	c[k] = 0
flag = false//有无解标志
graphcolor(1)
if flag == false:
	return "无解"
else:
	return c

def graphcolor(k):
	for color = 1 to 3:
		c[k] = color;
		if c 合法:
			flag = true
			return
		else if c 部分着色:
			graphcolor(k+1)//若此时k+1点的三个颜色都不符合，自动回溯到k点并继续执行for

迭代算法：

Input: 无向图G=(V, E).
Output: G的顶点的3-着色c[1…n]，其中每个c[j]是1、2或3。
for k = 1 to n:
	c[k] = 0
k = 1
while 1 <= k <= n :
	while c[k] <= 2:
		c[k] = c[k] + 1;
		if c 合法:
			return true
		else if c 部分着色:
			k++
	//如果三个颜色都不行，则回溯
	c[k] = 0
	k = k - 1
return "无解"

二、八皇后问题(The 8-Queens Problem)

在4X4格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

每种可能的配置都可以用四个分量x=（x1、x2、x3、x4）的向量来描述，其中xi表示第i行的皇后所在的列数。由此可以保证每个皇后不在同一行；若xi均不相同，则可以保证每个皇后不在同一列；且仅当：$x_i-x_j=i-j$或$x_i-x_j=j-i$时，皇后会在同一对角线。

搜索树的构建如下图所示：

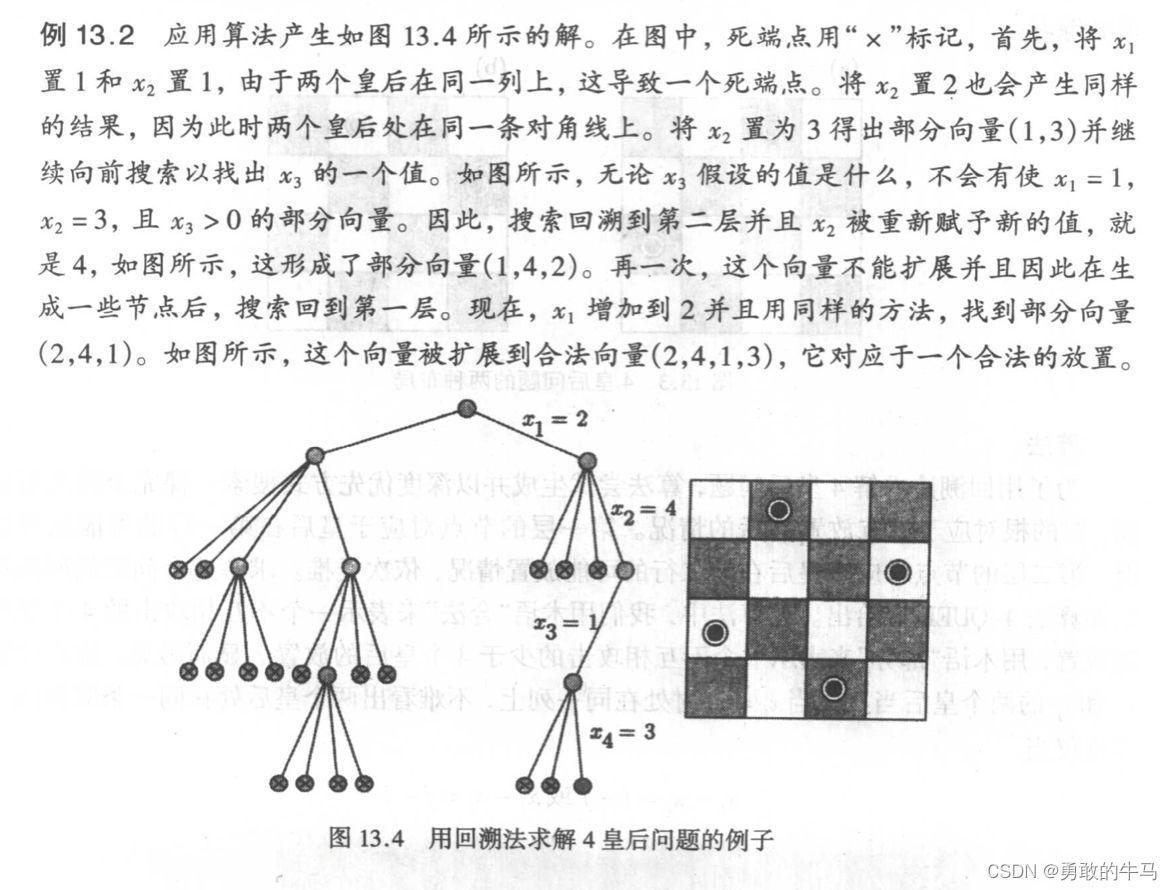
算法伪代码如下：

迭代算法：

Input: none
Output: 对应于4皇后问题解的向量x[1…4]。
for k = 1 to 4:
	x[k] = 0
k = 1
while 1 <= k <= 4 :
	while x[k] <= 3:
		x[k] = x[k] + 1;
		if x 合法:
			return true
		else if c 部分放置:
			k++
	//如果四个位置都不行，则回溯
	x[k] = 0
	k = k - 1
return "无解"

三、一般的回溯算法

四、分支定界(Branch and Bound)

当回溯搜索满足某些属性（包括最大化或最小化）的解或解集时，分枝定界算法通常只关注给定函数的最大化或最小化。此外，在分支定界算法中，在每个节点x上计算节点给出的任何解的可能值的定界，这些解随后可能在以x为根的子树中生成。如果计算的边界比上一个边界差，则以x为根的子树将被阻止扩展。

此后，我们将假设该算法是最小化给定的代价函数；最大化的情况也类似。对于所有部分解（partial solutions ）（x1，x2，…，xk-1）及其扩展（x1，x2，…，xk），我们必须满足：

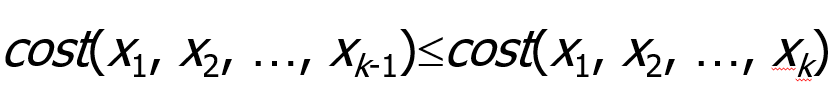
给定此属性，如果部分解（x1，x2，…，xk）的成本大于或等于先前计算的解，则该部分解（x1，x2，…，xk）在生成后可被丢弃。因此，如果该算法找到一个代价为c的解，并且存在一个代价至少为c的部分解，则不会生成该部分解的更多扩展。

利用分支定界法求解旅行商问题

给定一组城市和在每对城市上定义的成本函数，找到一个最小成本的旅游。在这里，旅游是一条封闭的路径，每座城市只访问一次。成本函数可以是距离、旅行时间、机票等。TSP的一个实例由其成本矩阵给出，其条目假定为非负数。

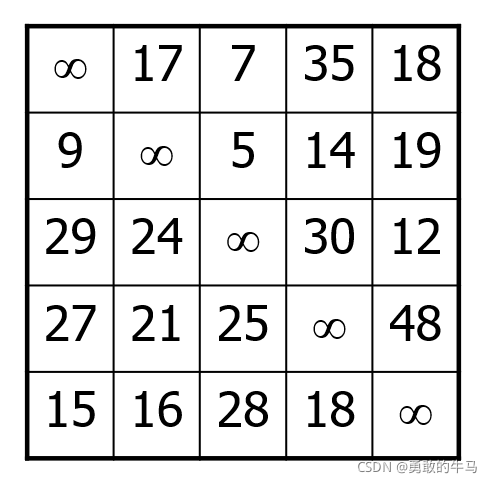
对于每个部分解（x1，x2，…，xk），我们关联一个下界y，它是按此顺序访问城市x1，x2，…，xk的任何完整旅行的成本必须至少为y。
我们观察到，每个完整的巡回必须包含成本矩阵中每行和每列的一条边及其相关成本。如果从成本矩阵A的任何行或列中的每个条目中减去常数r，则新矩阵下的任何旅行的成本正好比A下的相同旅行的成本低r。这激发了减少成本矩阵的想法，以便每行或每列至少包含一个等于0的条目。我们将这种矩阵称为原始矩阵的规约化（reduction）。

规约化矩阵如下图所示：

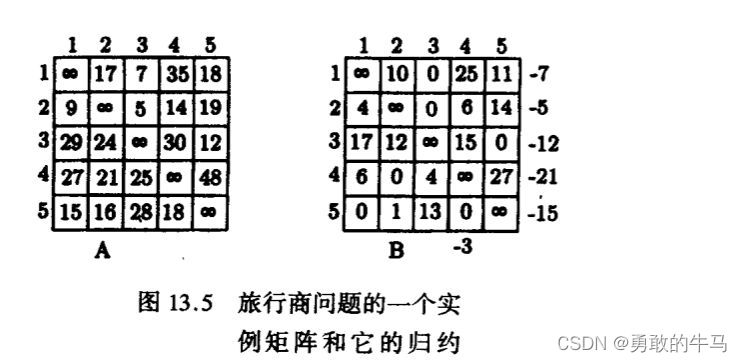
设（r1，r2，…，rn）和（c1，c2，…，cn）分别为n*n的成本矩阵A中从第1行到第n行和第1列到第n列中减去的金额，定义如下任何完整行程成本的下限y：

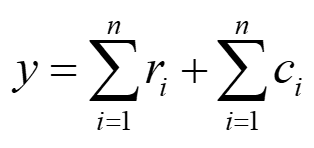
搜索树的构建如下图所示：

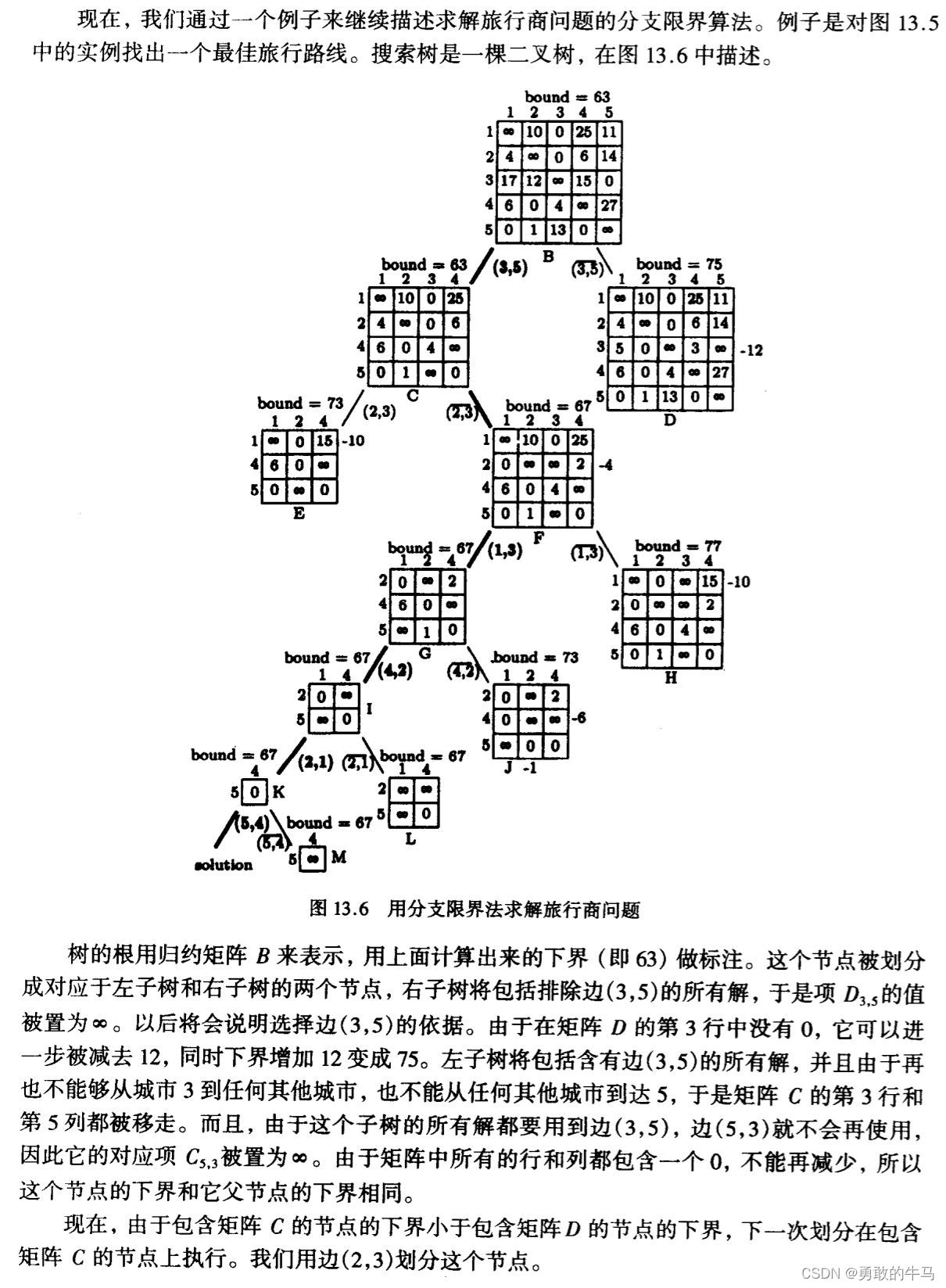
但此算法不能保证最优解。