【数学建模】【lingo】运输方案&连续投资

问题一

模型假设

1.假设运输过程中不会出现天气等影响货物数量的意外情况。
2.假设不会出现影响货物储备量的意外情况。

符号说明

限制条件

目标函数：

限制条件一：送到仓库的货物数量和要分别小于工厂产量：

限制条件二：要使得输送量等于顾客需求量：

限制条件三：由工厂送给仓库的货物量大于等于仓库送到顾客的货物量：

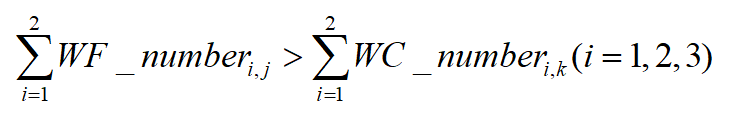
源代码

model:
title NJUCM第一次数模作业;

sets:
Factory/1..2/:production; ! j;
Warehouse/1..3/; ! i;
Customers/1..4/:needs; ! k;
link_1(Warehouse, Factory):W_F, WF_number; ! 将其理解为3 * 4维的数组(i, j);
link_2(Warehouse, Customers):W_C, WC_number; ! 将其理解为3 * 2维的数组(i, k);
endsets

data:
needs = 3, 5, 4, 5;
production = 10, 10;

W_F = 
4 3
2 1
5 2;

W_C = 
5 7 10 20
9 6 7 15
20 6 7 4; 
enddata

min = 
@sum(link_1(i, j) : W_F(i, j) * WF_number(i, j)) 
+
@sum(link_2(i, k) : W_C(i, k) * WC_number(i, k));

@for(Factory(j) : 
	@sum(Warehouse(i) : WF_number(i, j)) < production(j));
@for(Customers(k) :
	@sum(Warehouse(i) : WC_number(i, k)) = needs(k));
@for(Warehouse(i) :
	@sum(Factory(j) : WF_number(i, j)) > @sum(Customers(k) : WC_number(i, k)));

end

结果分析

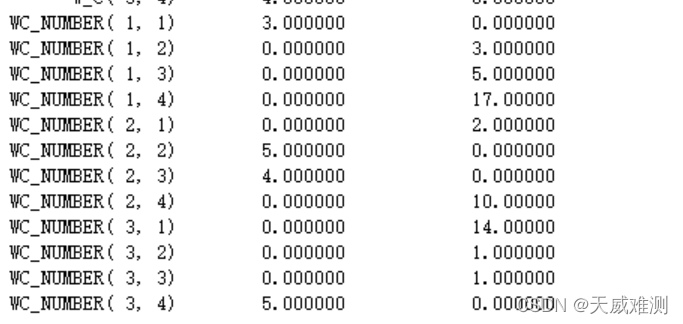
工厂A分别运给三个仓库货物3,4,0万个；
工厂B分别运给三个仓库货物0,5,5万个；

仓库A分别运给四名顾客3,0,0,0万个；
仓库B分别运给四名顾客0,5,4,0万个；
仓库C分别运给四名顾客0,0,0,5万个;

最终使得总运费最少为128万元

问题二

模型假设

1.假设在投资过程中不会出现金融波动等影响收益的情况。
2.假设在投资时不考虑纳税费用。
3.假设投资期间市场经济稳定，社会政策无比较大变化。
4.假设投资期间各项投资项目利率基本稳定。

限制条件

1.第一年的10万全部用于投资。
2.第二年初的投资为第一年末拿回来的钱。
3.第三、四、五年年初的投资分别等于前一年年末拿回来的钱。
4.B和C项目投资额分别不得超过4,3万元。

源代码

model:
title NJUCM第一次数模作业;

max = 1.15 * x4a + 1.25 * x3b + 1.40 * x2c + 1.11 * x5d;

x1a + x1d = 10;
x2a + x2c + x2d = 1.11 * x1d;
x2c < 3;
x3a + x3b + x3d = 1.15 * x1a + 1.11 * x2d;
x3b < 4;
x4a + x4d = 1.15 * x2a + 1.11 * x3d;
x5d = 1.15 * x3a + 1.11 * x4d;

end

结果分析

这边我想懒一下了，据吴日新学长所说，最好用三线表的形式来表达最终结果。