Linear Regression 吴恩达机器学习实验一（线性回归）

Linear Regression with one variable

实验要求

"""
在这部分练习中，您将使用一个变量实现线性回归，以预测食品卡车的利润。
假设你是一家餐厅特许经营公司的首席执行官，正在考虑在不同的城市开设新的分店。
该连锁店已经在各个城市拥有卡车，您可以从这些城市获得利润和人口数据。

您希望使用此数据来帮助您选择下一个要扩展到的城市。
文件ex1data1.txt包含线性回归问题的数据集。
第一列是一个城市的人口，第二列是该城市食品卡车的利润。利润为负值表示亏损。
"""

代码部分如下

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

加载数据集

data = pd.read_csv('ex1data1.txt',names = ['Population','Profit']) # names参数传递列表，将名字命名在对应列上
data_x = np.array(data['Population'])  # 将数据名为x的列提取
data_y = np.array(data['Profit'])  # 同上
data.head()  # 是指取数据的前n行数据，默认是前5行。

打印了前五行数据

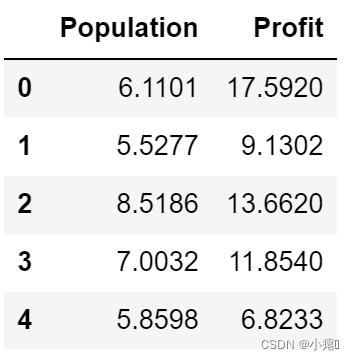
看看数据分布

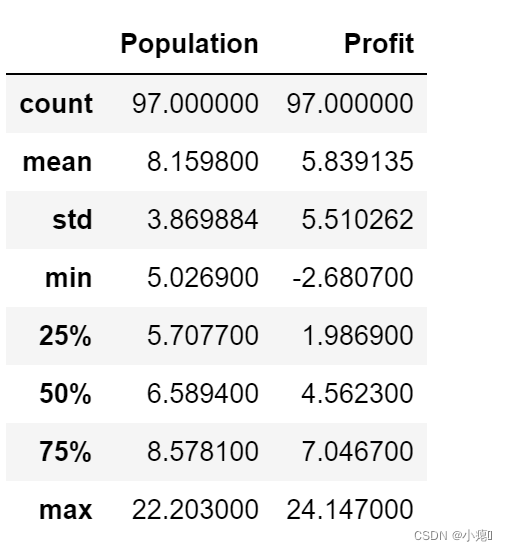
data.describe()  # count数据量 mean均值 std标准差 min最小值 max最大值

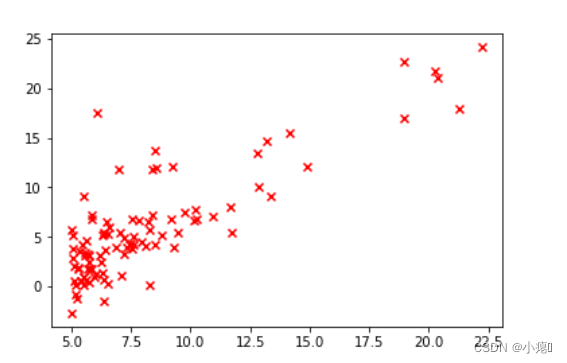
绘图观察数据在坐标上的分布。

目标：利用梯度下降，使代价函数代价最小化，从而使假设函数更好地拟合数据，完成线性回归从而作出新的预测。

下面是代价函数：
$$J\left(\theta \right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$

# 代价函数
def computeCost(X,y,theta):
    inner = np.dot(X,theta.T)
    result = np.sum(np.power(inner - y,2))
    return result/( 2 * len(X))

让我们在训练集中添加一列，保存theta0的占位符。
以便我们可以使用向量化的解决方案来计算代价和梯度。
在第0个列上建造一个新列’ones’,插入值1，方便后面计算时theta0的x系数为1.
因为：
$h(x)={\theta }_0+{\theta }_{1}x$

以下两式由梯度下降和代价函数求偏导数后求出。
${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$

${\theta }_1:={\theta }_1-a\frac{1}{m}\sum _{i=1}^m\left(\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\cdot x^{(i)}\right)$
所以：

data.insert(0,'Ones',1) 
data.head()

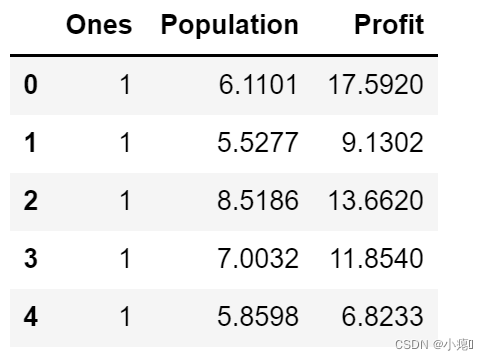
# 建立训练数据集X 和 目标变量y
cols = data.shape[1]
X = data.iloc[:,0:cols-1] # 因为提取是左闭右开原则[0,2)故将ones和人口给X
y = data.iloc[:,cols-1:cols] # 原理同上,必须打上开区间才行，否则维度不正确

这里可以用X.shape 和 y.shape检验一下维度。

这里初始化参数值，${\theta }_0{\theta }_1$ 的初值都是0.

# 初始化数据
theta = np.matrix(np.array([0,0]))
X = np.matrix(X)
y = np.matrix(y)

下面设置梯度下降算法：
这里的原理就是通过不断的迭代，通过误差来不断修改$\theta$参数的值，并且每一次迭代，都要保证代价cost的下降。直到cost最小（收敛）。最后的参数刚好可以使线性函数最好地拟合数据。

# 单变量梯度下降
def gradientDescent(X,y,theta,alpha,iters):
    temp = np.matrix(np.zeros(theta.shape)) # 创建一个和theta相同大小的临时变量矩阵
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)
    
    for i in range(iters):
        error = (X * theta.T) - y  # 建模误差
        for j in range(parameters):
            term = np.multiply(error , X[:,j]) # 建模误差与x样本对应相乘
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))# 矩阵访问下标
            
        theta = temp
        cost[i] = computeCost(X,y,theta)
    
    return theta , cost

对应公式：（1）先求偏导数：
$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}{\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$

$j=0$ 时：$\frac{\partial }{\partial {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$

$j=1$ 时：$\frac{\partial }{\partial {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m\left(\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\cdot x^{(i)}\right)$
（2）接下来对应公式
Repeat {

​ ${\theta }_0:={\theta }_0-a\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)$

​ ${\theta }_1:={\theta }_1-a\frac{1}{m}\sum _{i=1}^m\left(\left(h_{\theta }(x^{(i)})-y^{(i)}\right)\cdot x^{(i)}\right)$

​ }

error 对应：
$h_{\theta }(x^{(i)})-y^{(i)}={\theta }_0+{\theta }_{1}x-y^{(i)}$

term对应：
​ $\theta :=\theta -a\frac{1}{m}\sum _{i=1}^m\left(\left(\mathrm{error}\right)\cdot x^{(i)}\right)$

temp[0,j]应该对应上面公式很容易看出。这是一个更新临时变量的过程，这可以保证参数同时更新。
这里注意temp的类型是matrix类型，[0,j]表示访问矩阵的第0行第j列元素。

将代价存放在数组里方便后续运算和画图。

# 初始化参数
alpha = 0.01
iters = 1000

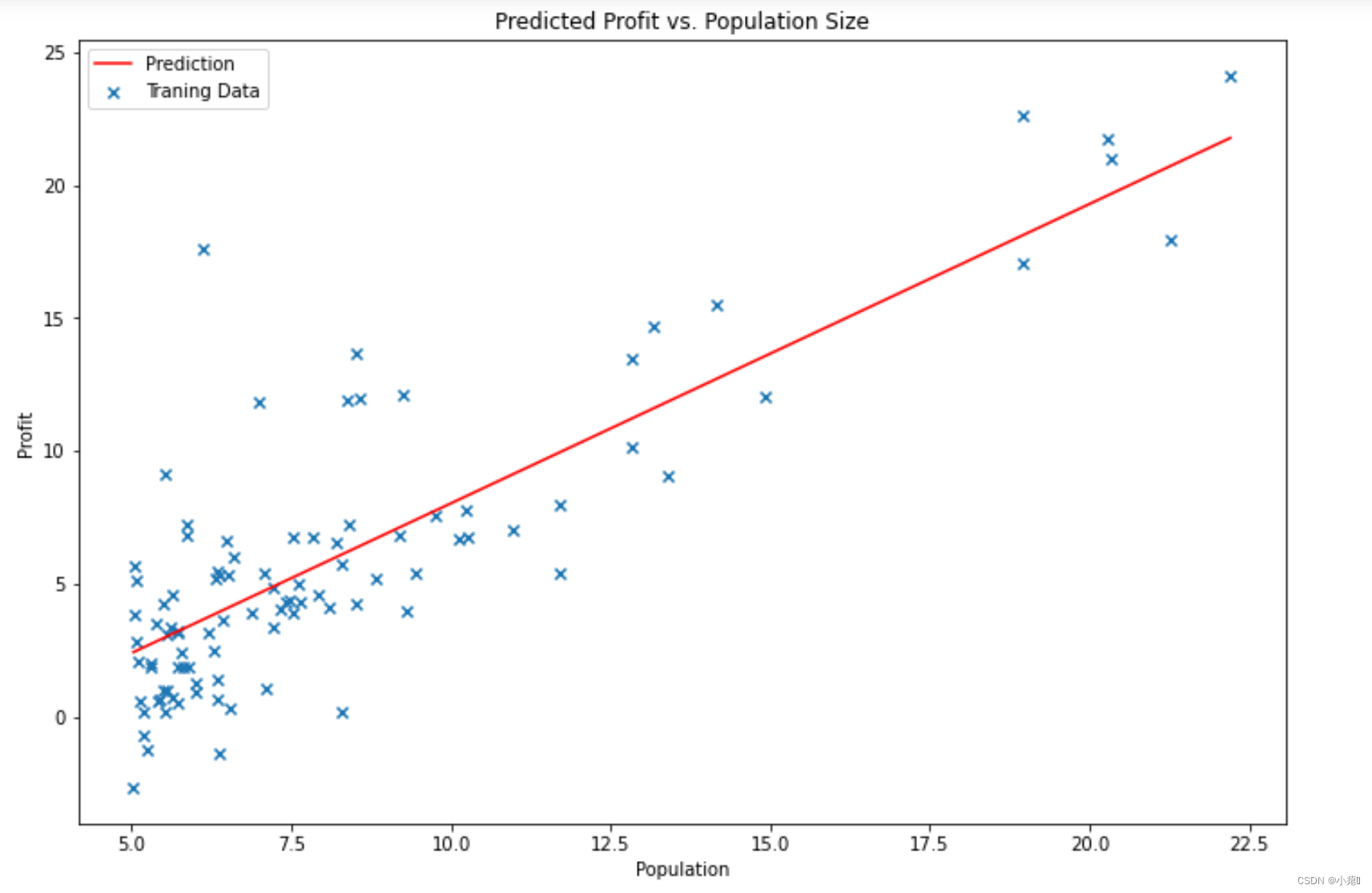
绘制图片：

x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x) # 假设函数

fig, ax = plt.subplots(figsize=(12,8)) # 建立一个图
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, marker = 'x', label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

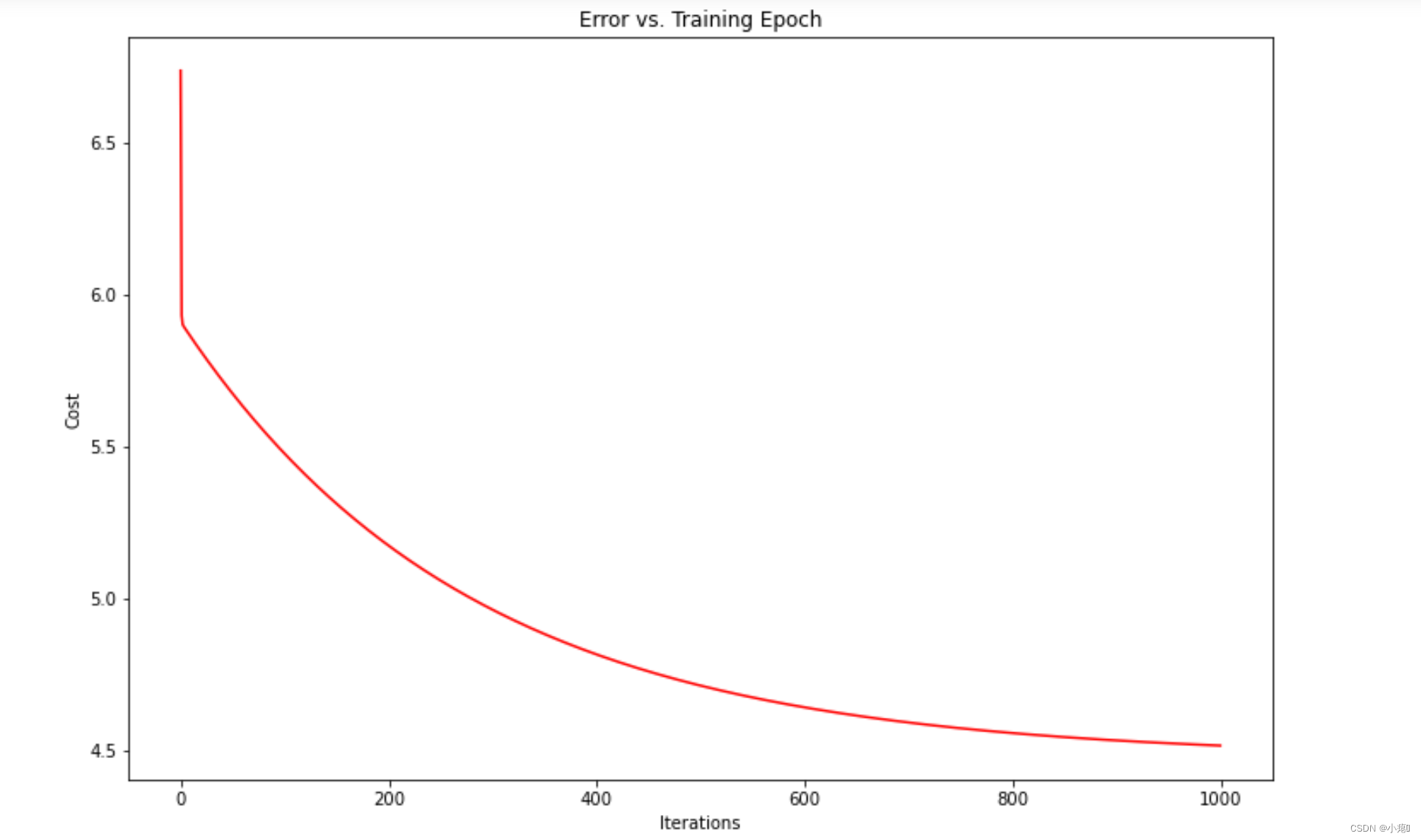
绘制cost图像观察收敛情况。

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

参考链接：
https://blog.csdn.net/weixin_40212554/article/details/89437146
https://www.zhihu.com/people/fengdu78

Linear Regression with Multivariable

"""
在这一部分中，您将使用多个变量实现线性回归，以预测房价。
假设你正在卖房子，你想知道好的市场价格是多少。
这样做的一个方法是首先收集近期售出房屋的信息，并制作房价模型。
ex1data2.txt文件包含俄勒冈州波特兰市房价的训练集。
第一列是房子的大小（平方英尺），第二列是卧室的数量，第三列是房子价格。
"""

data2 = pd.read_csv('ex1data2.txt',names = ['Size','Bedrooms','Price']) # names参数传递列表，将名字命名在对应列上
data2.head()  # 是指取数据的前n行数据，默认是前5行。

要进行数据预处理，这是实验要求：

# 因为样本数据范围大且分布不一致，所以使用特征归一化。
# 这部分是实验要求的：

#通过查看这些值，请注意房屋大小大约是卧室数量的1000倍。
#当特征相差几个数量级时，首先执行特征缩放可以使梯度下降收敛得更快
data2 = (data2 - data2.mean()) / data2.std()
data2.head()

# add ones column
data2.insert(0, 'Ones', 1)

# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]

# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))

# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)

# get the cost (error) of the model
computeCost(X2, y2, g2)

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()