空间滤波详解

        所谓空间滤波, 是指在光学系统的傅里叶频谱面上放置适当的滤波器, 改变光波的频谱结构, 使其像按照人们的要求实现变换.

一、空间滤波的基本原理

1.1 阿贝(Abbe)成像理论

二次衍射成像理论: 相干照明下, 成像过程可分作两步：

① 物平面上发出的光波经过透镜, 在其后焦面上产生夫琅和费衍射, 得到第一次衍射像;

② 该衍射像作为新的相干波源, 由它发出的次波在像平面上干涉而构成物体的像, 称为第二次衍射像。

        谱面上的光场分布与物的结构密切相关, ξ=x/f ——原点附近分布着物的低频信息; 离原点较远处, 分布着物的较高的频率分量。

1.2 阿贝-波特(Abbe – Porter)实验

阿贝-波特实验: 结论

（1）实验充分证明了阿贝成像理论的正确性: 像的结构直接依赖于频谱的结构, 只要改变频谱的组分, 便能够改变像的结构; 像 和物的相似程度完全取决于物体有多少频率成分能被系统传递到像面。

（2）实验充分证明了傅里叶分析和综合的正确性:

① 频谱面上的横向分布是物的纵向结构的信息; 频谱面上的纵向分布是物的横向结构的信息;

② 零频分量是直流分量, 它只代表像的本底

③ 阻挡零频分量,在一定条件下可使像的衬度发生反转

④ 仅允许低频分量通过时,像的边缘锐度降低;仅允许高频分量通过时,像的边缘效应增强;

⑤ 采用选择型滤波器,可望完全改变像的性质.

1.3 空间滤波的频谱分析

1.3.1 空间频率滤波系统

频谱分析: 观察和记录物的空间频率特性.

空间滤波: 改变物的空间频谱结构,进而改变像分布

改变滤波器的振幅透过率函数,可改变像的结构。

1.3.2 空间滤波的傅里叶分析

利用透镜的傅里叶变换性质分析阿贝-波特实验

讨论一维情况,并利用4f系统进行滤波操作

其透过率函数为

物置于4f系统输入面上,可在频谱面上得到它的傅里叶变换—栅状物的夫琅和费衍射图样:

强度呈现为一系列亮点,每个亮点是一个函数；

幅值受单缝衍射限制,包络是 单缝夫琅和费衍射图样；

中心分别位于ξ= m/d (m = 0 , +1 , +2 …）

滤波器采用狭缝或开孔式二进制(0 , 1)光阑,置于频谱面上

（1）滤波器是单一通光孔, 只允许零级通过

在滤波器后,仅有T (ξ)中的第一项通过,其余项均被挡住,因而频谱面后的光振幅为

输出平面上得到T (ξ) ꞏ F (ξ)的傅里叶逆变换

表示一个强度均匀的亮区,其振幅衰减为a/d,亮区宽度为L,与栅状物宽度相同,栅状结构完全消失,这与实验结果相符

零频分量是一个直流分量,它只代表像的本底。

只让0级,即直流成分通过,则像平面被0级斑发出的球面波照明. 近轴条件下,被均匀照明。

（2）狭缝加宽, 能使零级和正、负一级频谱通过

 像与物的周期相同,但振幅分布不同, 这是由于失去高频信息而造成边缘锐度消失的缘故.

让0级和±1级通过，则像平面上是0、±1三个衍射斑发出的次波的相干叠加。

（3）双缝滤波器,仅允许正、负二级频谱通过

滤波后的频谱函数取±2级的对应项, 即

则在输出平面的像场分布为

 在这种情况下, 像的结构是余弦振幅光栅, 但其周期为物周期的一半

（4）滤波器为一光屏, 只阻挡零级, 允许其它频谱通过

经过傅里叶变换后,像的分布是物分布减去物的平均值.有以下可能的情况:

(i)当a=d/2时,即栅状物的缝宽等于缝间隙时

 像的振幅分布具有周期性,其周期与物周期相同,但强度是均匀的,实际上看不到条纹

 (ii)当a>d/2时

 强度分布出现衬度反转,原来的亮区变为暗区,原来的暗区变为亮区.像的振幅分布向下错位。

二、 滤波器的种类及应用举例

2.1 振幅型滤波器

        只改变傅里叶频谱的振幅分布,不改变它的位相分布,通常用A (ξ , η)表示.它是一个振幅分布函数,其值可在0～1的范围内变化.

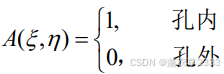
 根据不同的滤波频段又可分为低通、高通和带通三类.

低通滤波器: 用于滤去频谱中的高频部分,只允许低频通过.可用于滤除高频噪声等

        低通滤波器主要用于消除图像中的高频噪声,例如电视图像照片、新闻传真照片等往往含有密度较高的网点, 由于周期短、频率高,它们的频谱分布展宽.用低通滤波器可有效地阻挡高频成分,以消除网点对图像的干扰,但由于同时损失了物的高频信息而使像边缘模糊.

低通滤波: 激光系统空间滤波器

高通滤波器: 滤除频谱中的低频部分,以增强像的边缘,或实现衬度反转.高通滤波器主要用于增强模糊图像的边缘,以提高对图像的识别能力.由于能量损失较大,所以输出结果一般较暗.

带通滤波器: 选择某些频谱分量通过,阻挡另一些分量.可用于滤除随机噪声或突出某些方向的特征等

2.2 相位型滤波器ꞏ相衬显微镜

        相位型滤波器只改变傅里叶频谱的位相分布,不改变它的振幅分布,其主要功能是用于观察位相物体。

相位物体：物体各部分都是透明的,其位相变化反映为厚度或折射率的变化, 其透过率只包含位相分布函数:

一般无法通过成像进行观察和测量. 只有将相位信息变换为振幅信息,才有可能用肉眼直接观察到物体. 1935年泽尼克（Zernike）发明了相衬显微镜, 解决了相位到振幅的变换

位相滤波:泽尼克相衬显微镜

假设位相变化很小,可以进行泰勒展开:

若<<1，则可得到一级近似:（二者位相相差 , 互不干涉）

观察到的强度分布为:

弱的衍射项(x3,y3)湮没在强的非相干背景中.

要观察到与位相变化成正比的强度变化,必须改变二部分光场之间的位相正交关系.

方法:在谱面上用位相滤波器, 改变零频与其它频率成分之间的相对位相关系

滤波器函数：

经滤波后频谱为:

 

像面复振幅分布为：

强度分布为:

强度变化反映了位相变化,并且变化的幅度相对背景而言加倍, 但仍为线性变化

号代表正位相反衬和负位相反衬,前者表示位相越大,像强度越大,后者则相反.

如果在中心镀层中不但有位相变化而且有吸收,则可进一步提高像的对比度.

位相滤波器主要用于将位相型物转换成强度型像的显示